- はじめに(last modified 2014/05/14)
- 過去のお知らせ(last modified 2022/10/26)
- インストール | について (last modified 2015/04/02)
- インストール | R本体 | 最新版 | Win用 (last modified 2015/03/22)推奨
- インストール | R本体 | 最新版 | Mac用 (last modified 2015/04/01)推奨
- インストール | R本体 | 過去版 | Win用 (last modified 2015/03/22)
- インストール | R本体 | 過去版 | Mac用 (last modified 2015/03/22)
- インストール | Rパッケージ | ほぼ全て(20GB以上?!) (last modified 2015/03/22)
- インストール | Rパッケージ | 必要最小限プラスアルファ(数GB?!) (last modified 2017/03/08)推奨
- インストール | Rパッケージ | 必要最小限(数GB?!) (last modified 2015/05/25)
- インストール | Rパッケージ | 個別 (last modified 2015/10/17)
- (削除予定)Rのインストールと起動(last modified 2014/05/14)
- (削除予定)Rの昔のバージョンのインストール(last modified 2012/04/07)
- 使用例(初心者向け)(last modified 2011/09/15)
- サンプルデータ (last modified 2017/03/10)
- イントロ | 発現データ取得 | 公共DBから (last modified 2014/05/11)
- イントロ | 発現データ取得 | inSilicoDb(Taminau_2011) (last modified 2015/05/11)
- イントロ | 発現データ取得 | ArrayExpress(Kauffmann_2009) (last modified 2015/05/11)推奨
- イントロ | 発現データ取得 | GEOquery(Davis_2007) (last modified 2013/08/20)
- イントロ | アノテーション情報取得 | 公共DB(GEO)から (last modified 2013/08/18)
- イントロ | アノテーション情報取得 | GEOquery(Davis_2007) (last modified 2017/03/08)推奨
- イントロ | アノテーション情報取得 | Rのパッケージ*.dbから (last modified 2014/06/02)
- イントロ | プローブ配列情報取得 | Rのパッケージから (last modified 2013/08/16)
- イントロ | トランスクリプトーム配列取得 | biomaRt(Durinck_2009) (last modified 2013/09/18)推奨
- イントロ | トランスクリプトーム配列取得 | annotateパッケージ (last modified 2013/09/25)
- イントロ | Affymetrix CELファイル | 各種情報取得 (last modified 2013/09/04)
- 正規化(cDNA or two-color or 二色法) について(last modified 2008/03/31)
- 正規化 | Stanford型 (or cDNA)マイクロアレイ (package: limma)
- 正規化 | Stanford型 (or cDNA)マイクロアレイ (package: marray)
- 正規化 | Agilent microarray | について(last modified 2014/07/24)
- 正規化 | Agilent microarray | agilp(Chain_2010) (last modified 2013/05/30)
- 正規化 | Illumina BeadArray | について(last modified 2014/07/16)
- 正規化 | Illumina BeadArray | BeadDataPackR(Smith_2010) (last modified 2013/05/30)
- 正規化 | Illumina BeadArray | lumi(Du_2008) (last modified 2013/05/30)
- 正規化 | Illumina BeadArray | beadarray(Dunning_2007) (last modified 2013/05/30)
- 正規化 | Affymetrix GeneChip | について(last modified 2015/11/11)
- 正規化 | Affymetrix GeneChip | frma(McCall_2010) (last modified 2013/08/21)
- 正規化 | Affymetrix GeneChip | rmx(Kohl_2010) (last modified 2016/05/10)
- 正規化 | Affymetrix GeneChip | GRSN(Pelz_2008) (last modified 2013/05/27)
- 正規化 | Affymetrix GeneChip | Hook(Binder_2008) (last modified 2013/05/30)
- 正規化 | Affymetrix GeneChip | DFW(Chen_2007) (last modified 2022/04/17)
- 正規化 | Affymetrix GeneChip | FARMS(Hochreiter_2006) (last modified 2019/12/28)
- 正規化 | Affymetrix GeneChip | multi-mgMOS(Liu_2005) (last modified 2013/08/21)
- 正規化 | Affymetrix GeneChip | GCRMA(Wu_2004) (last modified 2013/08/21)
- 正規化 | Affymetrix GeneChip | PLIER(Affymetrix_2004) (last modified 2013/08/21)
- 正規化 | Affymetrix GeneChip | VSN(Huber_2002) (last modified 2013/08/21)
- 正規化 | Affymetrix GeneChip | RMA(Irizarry_2003) (last modified 2013/08/21)推奨
- 正規化 | Affymetrix GeneChip | MAS5.0(Hubbell_2002) (last modified 2013/11/25)
- 正規化 | Affymetrix GeneChip | MBEI(Li_2001) (last modified 2013/08/21)
- 前処理 | について(last modified 2013/11/13)
- 前処理 | スケーリング | サンプル間のシグナル強度の平均値をそろえる (last modified 2013/6/2)
- 前処理 | スケーリング | サンプル間のシグナル強度の中央値をそろえる (last modified 2013/6/2)
- 前処理 | スケーリング | 各サンプルのシグナル強度の平均を0、標準偏差を1にする (last modified 2013/6/2)
- 前処理 | スケーリング | 各遺伝子のシグナル強度の平均を0、標準偏差を1にする (last modified 2013/6/2)
- 前処理 | スケーリング | 各サンプル or 遺伝子のシグナル強度の平均を0、MADを1にする (last modified 2013/6/2)
- 前処理 | スケーリング | 各サンプル or 遺伝子のシグナル強度の中央値を0、標準偏差を1にする (last modified 2013/6/2)
- 前処理 | スケーリング | 各サンプル or 遺伝子のシグナル強度の中央値を0、MADを1にする (last modified 2013/6/2)
- 前処理 | スケーリング | 各サンプル or 遺伝子のシグナル強度のTukey biweightを0、MADを1にする (last modified 2013/6/2)
- 前処理 | スケーリング | 各サンプル or 遺伝子のシグナル強度の範囲を0-1にする (last modified 2013/6/2)
- 前処理 | スケーリング | シグナル強度を対数(log)変換する (last modified 2013/6/2)
- 前処理 | スケーリング | Quantile normalization(last modified 2013/09/11)
- 前処理 | フィルタリング | 低発現遺伝子を除去 (last modified 2013/11/14)
- 前処理 | フィルタリング | log比が小さいものを除去 (last modified 2013/11/15)
- 前処理 | フィルタリング | NAを含むものを除去 (last modified 2013/11/15)
- 前処理 | フィルタリング | CVが小さいものを除去 (last modified 2013/11/15)
- 前処理 | フィルタリング | 分散が小さいものを除去 (last modified 2013/11/15)
- 前処理 | ID変換 | について(last modified 2014/06/03)
- 前処理 | ID変換 | probe ID --> gene symbol(last modified 2017/09/22)
- 前処理 | ID変換 | probe ID --> Entrez ID(last modified 2014/06/03)
- 前処理 | ID変換 | probe ID --> その他(last modified 2014/06/03)
- 前処理 | ID変換 | 同じ遺伝子名を持つものをまとめる(last modified 2014/06/02)
- 解析 | 基礎 | 共通遺伝子の抽出(last modified 2013/06/02)
- 解析 | 基礎 | ベクトル間の距離(last modified 2013/11/22)
- 解析 | 基礎 | 遺伝子ごとの各種要約統計量の算出(last modified 2013/06/02)
- 解析 | 基礎 | 最大発現量を示す組織の同定(last modified 2013/06/02)
- 解析 | 基礎 | 似た発現パターンを持つ遺伝子の同定 (last modified 2013/06/02)
- 解析 | 基礎 | 平均-分散プロット (last modified 2013/11/25)
- 解析 | クラスタリング | について (last modified 2015/11/11)
- 解析 | クラスタリング | 階層的 | について (last modified 2016/05/25)
- 解析 | クラスタリング | 階層的 | pvclust (Suzuki_2006) (last modified 2010/08/05)
- 解析 | クラスタリング | 階層的 | hclust (last modified 2014/05/17)
- 解析 | クラスタリング | 階層的 | hclust後の詳細な解析 (last modified 2009/08/07)
- 解析 | クラスタリング | 階層的 | 最適なクラスター数を見積る (last modified 2009/09/09)
- 解析 | クラスタリング | 非階層的 | について (last modified 2015/11/11)
- 解析 | クラスタリング | 非階層的 | K-means
- 解析 | クラスタリング | 非階層的 | 自己組織化マップ(SOM)
- 解析 | クラスタリング | 非階層的 | 主成分分析(PCA) (last modified 2012/04/13)
- 解析 | 発現変動 | 2群間 | 発現変動遺伝子の割合を調べる | OCplus(Ploner_2006) (last modified 2015/11/11)
- 解析 | 発現変動 | 2群間 | 対応なし | について (last modified 2015/11/11)
- 解析 | 発現変動 | 2群間 | 対応なし | RankProd 2.0 (Del Carratore_2017) (last modified 2019/03/16)
- 解析 | 発現変動 | 2群間 | 対応なし | WAD (Kadota_2008) (last modified 2015/03/30)
- 解析 | 発現変動 | 2群間 | 対応なし | Random forest (Diaz-Uriarte_2007) (last modified 2013/06/02)
- 解析 | 発現変動 | 2群間 | 対応なし | shrinkage t (Opgen-Rhein_2007) (last modified 2013/06/02)
- 解析 | 発現変動 | 2群間 | 対応なし | layer ranking algorithm (Chen_2007) (last modified 2013/06/02)
- 解析 | 発現変動 | 2群間 | 対応なし | fdr2d (Ploner_2006) (last modified 2013/06/02)
- 解析 | 発現変動 | 2群間 | 対応なし | IBMT (Sartor_2006) (last modified 2014/02/03)
- 解析 | 発現変動 | 2群間 | 対応なし | Rank products (Breitling_2004) (last modified 2016/08/30)非推奨
- 解析 | 発現変動 | 2群間 | 対応なし | empirical Bayes (Smyth_2004) (last modified 2016/05/19)
- 解析 | 発現変動 | 2群間 | 対応なし | samroc (Broberg_2003) (last modified 2014/02/03)
- 解析 | 発現変動 | 2群間 | 対応なし | SAM (Tusher_2001) (last modified 2014/02/03)
- 解析 | 発現変動 | 2群間 | 対応なし | Student's t-test(last modified 2014/05/25)
- 解析 | 発現変動 | 2群間 | 対応なし | Welch t-test(last modified 2014/05/23)
- 解析 | 発現変動 | 2群間 | 対応なし | Mann-Whitney U-test(last modified 2013/10/15)
- 解析 | 発現変動 | 2群間 | 対応なし | パターンマッチング法(last modified 2014/05/23)
- 解析 | 発現変動 | 2群間 | 対応あり | について(last modified 2009/11/11)
- 解析 | 発現変動 | 2群間 | 対応あり | SAM (Tusher_2001) (last modified 2014/06/02)
- 解析 | 発現変動 | 2群間 | 対応あり | SAM (Tusher_2001)+WADの重みづけ (last modified 2013/06/02)
- 解析 | 発現変動 | 2群間 | 対応あり | 時系列 |について(last modified 2013/6/8)
- 解析 | 発現変動 | 2群間 | 対応あり | 時系列 | maSigPro (Conesa_2006) (last modified 2013/6/2)
- 解析 | 発現変動 | 3群間 | 対応なし | について(last modified 2015/01/16)
- 解析 | 発現変動 | 3群間 | 対応なし | Mulcom (Isella_2011)(last modified 2013/12/06)
- 解析 | 発現変動 | 3群間 | 対応なし | 基礎 | limma (Ritchie_2015)(last modified 2015/06/08)
- 解析 | 発現変動 | 3群間 | 対応なし | 応用1 | limma (Ritchie_2015)(last modified 2015/06/08)
- 解析 | 発現変動 | 3群間 | 対応なし | 応用2 | limma (Smyth_2004)(last modified 2015/06/08)
- 解析 | 発現変動 | 3群間 | 対応なし | 一元配置分散分析(One-way ANOVA)(last modified 2013/11/12)
- 解析 | 発現変動 | 3群間 | 対応なし | Kruskal-Wallis(クラスカル-ウォリス)検定 (last modified 2013/6/2)
- 解析 | 発現変動 | 多群間 | について(last modified 2013/6/2)
- 解析 | 発現変動 | 多群間 | SpeCond(Cavalli_2011) (last modified 2013/6/10)
- 解析 | 発現変動 | 多群間 | ROKU(Kadota_2006) (last modified 2014/05/30)
- 解析 | 発現変動 | 多群間 | Sprent's non-parametric method(Ge_2005) (last modified 2009/07/31)
- 解析 | 発現変動 | 多群間 | Schug's H(x) statistic(Schug_2005) (last modified 2011/10/13)
- 解析 | 発現変動 | 多群間 | Schug's Q statistic(Schug_2005) (last modified 2009/07/31)
- 解析 | 発現変動 | 多群間 | Ueda's AIC-based method(Kadota_2003) (last modified 2009/07/31)
- 解析 | 発現変動 | 多群間 | パターンマッチング法(テンプレートマッチング法) (last modified 2012/05/28)
- 解析 | 発現変動 | 時系列 | について(last modified 2013/6/10)
- 解析 | 発現変動 | 時系列 | Periodic genes | M-estimator (Ahdesmaki_2007) (last modified 2009/8/3)
- 解析 | 発現変動 | 時系列 | Periodic genes | Lomb-Scargle periodogram (Glynn_2006) (last modified 2006/7/11)
- 解析 | 発現変動 | 時系列 | non-periodic genes | randomized BHC (Darkins_2013) (last modified 2013/6/10)
- 解析 | 発現変動 | 時系列 | non-periodic genes | IPCA (Yao_2012) (last modified 2013/6/10)
- 解析 | 発現変動 | 時系列 | non-periodic genes | gptk (Kalaitzis_2011) (last modified 2013/6/10)
- 解析 | 発現変動 | 時系列 | non-periodic genes | betr (Aryee_2009) (last modified 2012/05/29)
- 解析 | 発現変動 | 時系列 | non-periodic genes | maSigPro (Conesa_2006) (last modified 2015/08/16)
- 解析 | 発現変動 | 時系列 | non-periodic genes | SAM (Tusher_2001) (last modified 2015/08/16)
- 解析 | 機能解析 | 遺伝子オントロジー(GO)解析 | について(last modified 2018/06/22)
- 解析 | 機能解析 | 遺伝子オントロジー(GO)解析 | GSAR (Rahmatallah_2017)(last modified 2017/05/11)
- 解析 | 機能解析 | 遺伝子オントロジー(GO)解析 | gage (Luo_2009)(last modified 2015/05/25)
- 解析 | 機能解析 | 遺伝子オントロジー(GO)解析 | GSA (Efron_2007)(last modified 2017/03/07)推奨
- 解析 | 機能解析 | 遺伝子オントロジー(GO)解析 | Category (Jiang_2007)(last modified 2014/06/01)
- 解析 | 機能解析 | 遺伝子オントロジー(GO)解析 | pcot2 (Kong_2006)(last modified 2014/06/01)
- 解析 | 機能解析 | 遺伝子オントロジー(GO)解析 | SAFE (Barry_2005)(last modified 2014/06/01)
- 解析 | 機能解析 | 遺伝子オントロジー(GO)解析 | globaltest (Goeman_2004)(last modified 2014/06/01)
- 解析 | 機能解析 | パスウェイ(Pathway)解析 | について(last modified 2018/06/22)
- 解析 | 機能解析 | パスウェイ(Pathway)解析 | GSAR (Rahmatallah_2017)(last modified 2017/03/12)
- 解析 | 機能解析 | パスウェイ(Pathway)解析 | Pathview (Luo_2013)(last modified 2014/06/01)
- 解析 | 機能解析 | パスウェイ(Pathway)解析 | gage (Luo_2009)(last modified 2016/05/25)
- 解析 | 機能解析 | パスウェイ(Pathway)解析 | SPIA (Tarca_2009)(last modified 2014/06/01)
- 解析 | 機能解析 | パスウェイ(Pathway)解析 | GSA (Efron_2007)(last modified 2017/03/08)推奨
- 解析 | 機能解析 | パスウェイ(Pathway)解析 | sigPathway (Tian_2005)(last modified 2014/06/01)
- ...
- 解析 | 機能解析(GSEA周辺)について(以下は再編予定)(last modified 2014/06/01)
- 解析 | 機能解析 | PAGE法(Kim_2005;統計量の変換なし)の考え方について (last modified 2009/9/11)
- 解析 | 機能解析 | PAGE法(Kim_2005;統計量の変換なし)を用いてGene Ontology解析 (last modified 2009/11/19)
- 解析 | 機能解析 | PAGE法(Kim_2005;統計量の変換あり)を用いてGene Ontology解析 (last modified 2009/10/27)
- 解析 | 機能解析 | PAGE法(Kim_2005)を用いてGene Ontology解析した結果をQuickGOにかける (last modified 2009/9/15)
- 解析 | 機能解析 | PAGE法(Kim_2005;統計量の変換なし)を用いてPathway解析 (last modified 2009/11/19)
- 解析 | 機能解析 | PAGE法(Kim_2005;統計量の変換あり)を用いてPathway解析 (last modified 2009/10/27)
- 解析 | 機能解析 | PAGE法(Kim_2005)を用いてPathway解析した後 (last modified 2009/10/27)
- 解析 | 機能解析 | PAGE(Z-score)法(Kim_2005;統計量の変換なし)を用いてGene Ontology解析 (last modified 2011/10/27)
- 解析 | 機能解析 | Parametric Gene Set Enrichment Analysis (PGSEA) (Kim_2005) (last modified 2009/6/1)
- 解析 | 分類 | k-Nearest Neighbor (k-NN)(last modified 2007/04/25)
- 解析 | 分類 | Self-Organizing Maps (SOM)
- 解析 | 分類 | Support Vector Machine (SVM) (last modified 2007/04/18)
- 解析 | 分類 | Naive Bayesian (NB)
- 解析 | アレイCGH(DNAコピー数)解析 | について(last modified 2014/07/24)
- 解析 | アレイCGH(DNAコピー数)解析 | ADaCGH (Diaz-Uriarte_2007) (last modified 2009/12/08)
- 解析 | アレイCGH(DNAコピー数)解析 | GLAD (Hupe_2004) (last modified 2009/12/08)
- 解析 | アレイCGH(DNAコピー数)解析 | DNAcopy (Olshen_2004) (last modified 2009/12/8)
- 作図 | M-A plot (last modified 2013/07/04)
- 作図 | ヒートマップ | 1. 感覚をつかむ (last modified 2015/10/17)
- 作図 | ヒートマップ | 2. 色を自在に変える(col) (last modified 2015/10/17)
- 作図 | ヒートマップ | 3. データを変換してから表示(scale) (last modified 2015/10/16)
- 作図 | ヒートマップ | 4. 余白を変える(margins) (last modified 2015/11/10)
- 作図 | ヒートマップ | 5. 大きさを変える(cex) (last modified 2015/10/16)
- 作図 | ROC曲線(ROC curve) (last modified 2013/11/14)
- Links(last modified 2012/04/25)
はじめに
このページは、マイクロアレイ(microarray)データ取得後のデータ解析をRで行うための一連の手続きをまとめたものであり、特にアグリバイオインフォマティクス教育研究プログラムの被養成者向けに作成したものです。
Maintainerは門田幸二(東京大学大学院農学生命科学研究科)が永らく一人でやっていましたが、 2013年7月のリニューアル以降は私の出身研究室(東京大学・大学院農学生命科学研究科・応用生命工学専攻・生物情報工学研究室: 清水謙多郎教授)大学院生の孫建強氏が W3C validation、美しいコーディング、TCCパッケージ開発および有用関数のTCCへの追加など重要な役割を担っています。
また、私がこの仕事にこれだけの時間を費やせるのは、ボスである清水謙多郎教授の全面的なサポートのおかげです。
実験研究者の方々は、Rを使うとよさそうだということはわかってはいても敷居が高いためなかなか踏み込めないという人が多いことと思います。そこで、教育に携わる身として、これまでRにパッケージを提供してこられた諸氏の有用なプログラムとその使用例をこのページであらためて紹介することを通じて、実験研究者自身がよりよいマイクロアレイデータ解析を自力で行えるための一助になればと思っています。コピペで結果が出せます!
以下は、原著論文やRパッケージのvignetteなどから得た情報をまとめたものです。本当に正しいやり方かどうかなど一切の保証はできませんので予めご承知おきください。このページの中身自体は、所属機関とは一切関係ない一個人の備忘録のようなものです。が、所属機関の私の担当する大学院講義や講習会などで利用しています。
間違いや修正点、また「このような解析をやりたいがどうすればいいか?」などのリクエストがあればメール( )をいただければ幸いです。特にアグリバイオインフォマティクス教育研究プログラム被養成者からのリクエストは優先的に対応します。
)をいただければ幸いです。特にアグリバイオインフォマティクス教育研究プログラム被養成者からのリクエストは優先的に対応します。
ここで紹介した様々な方法のほかにも多数の紹介しきれていないものがあります。それらはBioconductorのAll Packagesから辿れます(2013/07/19現在、Bioconductor version 2.12で672個のパッケージがあります)。これらの開発や普及に携わっている諸氏に御礼申し上げます。
このページ内で用いる色についての説明:
コメント 特にやらなくてもいいコマンド プログラム実行時に目的に応じて変更すべき箇所 実行結果を表示(アンダーラインがついてるほうはリンクです。)
過去のお知らせ
- 2022年
- 「実験医学別冊 論文図表を読む作法」が出版されています。タイトル通りですが、私個人としてはAccumulation curveの解説を入れていただいて大変助かっております。これまでなかなかとっつきにくかった図の理解が進む良書だと思います。(2022/07/27)
- 「正規化 | Affymetrix GeneChip | DFW(Chen_2007)」を更新しました。しばらく使えなかったのですが、使えるやり方を掲載しました(中井雄治 氏提供情報)。正確にはとっくに情報提供いただいていたのですが、多忙のためずっと気にはなっていたものの反映できずにおりましたm(_ _)m(2022/04/17)
- 東京大学・大学院農学生命科学研究科・応用生命工学専攻の令和5(2023)年度大学院学生募集公開ガイダンスは、2022年5月7日(土)と5月28日(土)に開催します。(2022/04/17)
- 2021年
- 独習 Pythonバイオ情報解析が2021年3月に出版されています。一般的なプログラミング言語として解説から、塩基配列データの取り扱い、データの可視化、そしてRNA-seq解析周辺など、非常に豊富な内容となっています。編集代表の黒川顕先生にはNGSハンズオン講習会の最終年度でお世話になり、執筆者の多くの先生にはアグリバイオインフォマティクス教育研究プログラム関連講義でもお世話になっております。(2021/03/27)
- Dr.Bonoの生命科学データ解析 第2版が2021年3月に出版されています(バイオインフォマティクス初学者向けの本)。前回の第1版から3年以上経過しており、WindowsでのLinux環境(WSL2)の話など最新情報にアップデートされているのが基本形です。しかし、大枠として変わってない部分もさらっとでも読むとよいと思います。第1版当時の自分には無縁で記憶に残っていない事柄でも、今の自分と関係があるかもしれないからです(私の場合はそれがオーソログクラスターでした)。(2021/03/18)
- 令和3年度のアグリバイオインフォマティクス教育研究プログラムに関する情報をトップページに掲載しています。(2021/03/18)
- single-cell RNA-seq (scRNA-seq)の解析パイプラインのガイドラインに関する論文であるVieth et al., Nat Commun., 2019についての批評論文が公開されました (Kadota and Shimizu, Front Genet., 2020)。特にscRNA-seqをbulk RNA-seqと差別化する際の論法や、 比較対象として用いたbulk RNA-seq用の正規化法の選定に関して、論文調査不足・事実誤認・ミスリード・不誠実さといった観点で痛烈に批判しています。(2020/07/28)
- 諸般(主にコロナに対する東大の全体方針)の事情により、2020年のアグリバイオインフォマティクス教育研究プログラムは、 東京大学の学生に限定することとなりました(2020年3月17日決定)。既に応募いただいた方、そしてこれから応募しようと思っていた方々には残念なお知らせとなってしまいましたが、 ご理解いただけますと幸いですm(_ _)m (2020/03/17)
- 「正規化 | Affymetrix GeneChip | FARMS(Hochreiter_2006)」において、関数名をq.farmsからqFarmsに、そしてl.farmsからlFarmsに変更しました。(中井雄治 氏提供情報)。(2019/12/28)
- 「生命科学者のためのDr.Bonoデータ解析実践道場(著:坊農秀雅)」が出版されています。 今回の"Bono本"は、アグリバイオの大学院講義で丁寧に教えることが現実的に難しいLinux環境でのデータ解析の情報が丁寧に解説されています(アグリバイオの内容と相補的な関係)。 「聞いたことはあるがよく知らない事柄」が簡潔かつ丁寧に書かれているので、私は主にそのあたりの頭の整理に利用させてもらっています。(2019/09/30)
- 「進化で読み解く バイオインフォマティクス入門(著:長田直樹)」が出版されています。 本書の何よりも素晴らしいところは、単著だという点だと思います(統一感って重要)。そしてチャラチャラしたところがなく、中身がしっかりしており、 そして幅広い内容が丁寧に解説されているという点が非常によいと思います。(2019/07/05)
- 「正規化 | Affymetrix GeneChip | rmx(Kohl_2010)」(の例題2)を実行する際に、R 3.6.0とR 3.5.1でエラーが出ることを確認しました。 回避策としては、「正規化 | Affymetrix GeneChip | RMA(Irizarry_2003)」をご利用ください(坂井星辰 氏提供情報)。(2019/06/18)
- 「解析 | 発現変動 | 2群間 | 対応なし | Rank products (Breitling_2004)」でエラーが出るというお知らせをいただきました(橋詰 力 氏 提供情報)。 調査の結果、RankProd 2.0 (Del Carratore et al., 2017)にバージョンが上がっていることが判明しました。 新設した「解析 | 発現変動 | 2群間 | 対応なし | RankProd 2.0 (Del Carratore_2017)」のほうをご利用下さい。少なくともエラーは出ずに、妥当な結果であるところまでは確認しました。(2019/03/17)
- 2018年11月に「よくわかるバイオインフォマティクス入門(藤博幸 編)」という本が出ました。(2018/11/21)
- 「解析 | 機能解析 | 遺伝子オントロジー(GO)解析 | について」を更新しました。(2018/06/22)
- 「解析 | 機能解析 | パスウェイ(Pathway)解析 | について」を更新しました。(2018/06/22)
- 「前処理 | ID変換 | probe ID --> gene symbol」の例題2以降のコードを改良しました。 具体的には、例えば例題2において、「2つの入力ファイルの1列目のprobe ID情報の対応がとれる(同じ行の位置でなくてもよい)ことが前提です」 のように書いていましたが、実際には同じ行の位置でなければいけなかったことが判明したので、例題2以降のコードについてバグの修正を行いました(川路啓太氏 提供情報)。(2017/09/22)
- お知らせは主に(Rで)塩基配列解析で行っておりますのでそちらをご覧ください。 マイクロアレイ関連の講義や講演資料なども(Rで)塩基配列解析中の参考資料(講義、講習会、本など)から辿れます。(2014/05/15)
- 平成29年度NGSハンズオン講習会の ウェブページが公開されました。受講申込の受付期間は2017年5月15日(月)14時00分~6月23日(金)12時00分です。(2017/05/15)
- 「解析 | 機能解析 | パスウェイ(Pathway)解析 | GSAR (Rahmatallah_2017)」を追加しました。 比較するグループ間で発現の異なる遺伝子セットを検出するだけでなく、ネットワーク図やグループごとの最有力遺伝子(most influential genes or hub genes)も示してくれます。(2017/03/12)
- 「解析 | 発現変動 | 2群間 | 対応なし | Rank products (Breitling_2004)」 の例題3の下のほうで書いていた「log(G2/G1)列:log比(G2の算術平均 - G1の算術平均)値」に関する注釈を追加しました。(2016/08/30)
- 私の所属するアグリバイオインフォマティクス教育研究プログラムでは、平成29年度もバイオインフォ関連講義を行います。 例年東大以外の企業の方、研究員、大学院生が2-3割程度受講しております。受講ガイダンスは4月5日17:15- 於東大農です。 例年アグリバイオ所有ノートPCは台数が絶対的に足りないので、特に外部の受講希望者はできるだけ基本的に3時間以上バッテリーがもつノートPCを用意して臨んで下さい。(2017/02/20)
- 門田幸二 著シリーズ Useful R 第7巻 トランスクリプトーム解析刊行(共立出版)。 マイクロアレイ解析に関する最近の知見や、ROKU法 (Kadota et al., 2006)、WAD法 (Kadota et al., 2008)などについての解説も含んでいます。 書籍中のマイクロアレイ解析部分のRコードについては、このページの「書籍 | トランスクリプトーム解析 | ...」に掲載してあります。(2014/04/27)
- (かなり先の話ですが...)平成26年3月7日に東京お台場にて、HPCIチュートリアルの一部としてRでゲノム・トランスクリプトーム解析を行います。情報はかなりアップデート予定です、、、が既に満席なようですいません。。。(2013/11/25)
- 「(Rで)塩基配列解析」もリニューアルしました。(2013/07/30)
- どのブラウザからでもエラーなく見られる(W3C validation)ようにリニューアルしました。(2013/07/19)
- 2013年7月18日まで公開していた以前の「(Rで)マイクロアレイデータ解析」のウェブページや関連ファイルはRdemicroarray.zipからダウンロード可能です(88MB程度)。(2013/07/19)
- 私の所属するアグリバイオインフォマティクス教育研究プログラムでは、平成25年度も(東大生に限らず)バイオインフォ関連講義を行います。受講希望者は平成25年4月5日17:15-18:00に東大農学部二号館二階化学第一講義室にて開催予定の受講ガイダンスに出席してください。 例年東大以外の企業の方、研究員、学生が二割程度は受講しております。 このウェブページ関連講義は「オーム情報解析」、それ以外の私の担当講義は「ゲノム情報解析基礎」と「農学生命情報科学特論I」です。興味ある科目のみの受講も可能ですので、お気軽にどうぞ。(2013/03/19)
- アグリバイオインフォマティクス教育研究プログラムでは特任研究員の募集をしています(締切3/15)。(2013/02/18)
- 遺伝子セット解析の一つであるGSA (Efron_2007)が一通りできるようになりました(2012/06/08)
インストール | について
本ウェブページの2015年3月下旬までの推奨インストール手順Rのインストールと起動は、 20GB程度のHDD容量(2015年3月調べ)を必要とすること、そしてそれに伴いインストールにかかる時間、インストールするパッケージ数の増大に伴うエラー遭遇率の上昇のため、 東大有線LANでもストレスを感じるようになってきました。そのため、 ユーザごとのネットワーク環境にも配慮した様々な選択肢を2015年3月末に提供し、推奨手順を変更しました(正確には2011年ごろの推奨手順に戻しました)。 私の環境は、Windows PCは(Windows 7; 64 bit)、Macintosh PCはMacBook Pro (OS X Yosemite ver. 10.10; 64 bit)です。 「自分の環境は32 bitなんだけど、何ができて何ができないか教えて」的な質問には答えられません。 R Studioというものもありますが、私は普段使いません。 「インストール | Rパッケージ | 」で必要最小限のパッケージインストールにとどめるようにすれば R Studioでもいいかもしれませんが、自己責任でご自由にお使いください。 以下は、「R本体の最新版」と「必要最小限プラスアルファ(数GB?!)」の推奨インストール手順をまとめたものです。
- Windows版(R_install_win.pdf; 2015.04.01版)
- Macintosh版(R_install_mac.pdf; 2015.04.02版)
インストール | R本体 | 最新版 | Win用
最新版(リリース版のこと)は、下記手順を実行します。インストールが無事完了したら、 デスクトップに「R i386 3.X.Y (32 bitの場合; XやYの数値はバージョンによって異なります)」 または「R x64 3.X.Y (64 bitの場合)」アイコンが作成されます。 私は「R i386 3.X.Y」のアイコンは使わないので、いつもゴミ箱に捨てています。 「R x64 3.X.Y」アイコンのほうのみ利用しています。 尚、エンドユーザには実質的に無縁のものだと思いますが開発版(devel版)というのもあります。
- Rのインストーラを「実行」
- 聞かれるがままに「次へ」などを押してとにかくインストールを完了させる
- 「コントロールパネル」−「デスクトップのカスタマイズ」−「フォルダオプション」−「表示(タブ)」−「詳細設定」のところで、 「登録されている拡張子は表示しない」のチェックを外してください。
インストール | R本体 | 最新版 | Mac用
最新版(リリース版のこと)は、下記手順を実行します。インストールが無事完了したら、 Finderを起動して、左のメニューの「アプリケーション」をクリックすると、Rのアイコンが作成されていることが確認できます。 Win同様、エンドユーザには実質的に無縁のものだと思いますがMacにも開発版(devel版)というのがあります。
- http://cran.r-project.org/bin/macosx/の「R-3.X.Y-marvericks.pkg」をクリック。 (XやY中の数値はバージョンによって異なります)
- ダウンロードしたファイルをダブルクリックして、聞かれるがままに「次へ」などを押してとにかくインストールを完了させる
- 「Finder」-「環境設定」-「詳細」タブのところで「すべてのファイル名拡張子を表示」にチェックを入れる。
インストール | R本体 | 過去版 | Win用
昔のバージョンをインストールしたい局面もごく稀にあると思います。 その場合は、ここをクリックして、 任意のバージョンのものをインストールしてください。例えば、2014年10月リリースのver. 3.1.2をインストールしたい場合は、 3.1.2をクリックして、 「Download R 3.1.2 for Windows」 をクリックすれば、後は最新版と同じです。
インストール | R本体 | 過去版 | Mac用
昔のバージョンをインストールしたい局面もごく稀にあると思います。 その場合は、ここをクリックして、 任意のバージョンのものをインストールしてください。例えば、2014年10月リリースのver. 3.1.2をインストールしたい場合は、 ページ下部の「R-3.1.2-marvericks.pkg」 をクリックすれば、後は最新版と同じです。
インストール | Rパッケージ | ほぼ全て(20GB以上?!)
Rパッケージの2大リポジトリであるCRANとBioconductor 中のほぼすべてのパッケージをインストールするやり方です。 パソコンのHDD容量に余裕があって、数千個ものパッケージ(20GB程度分)を数時間以上かけてダウンロードしてインストールできる環境にある方は、 R本体を起動し、以下を「R コンソール画面上」でコピー&ペースト。 どこからダウンロードするか?と聞かれるので、その場合は自分のいる場所から近いサイトを指定しましょう。
install.packages(available.packages()[,1], dependencies=TRUE)#CRAN中にある全てのパッケージをインストール source("http://www.bioconductor.org/biocLite.R")#おまじない biocLite(all_group()) #Bioconductor中にある全てのパッケージをインストール
インストール | Rパッケージ | 必要最小限プラスアルファ(数GB?!)
(Rで)塩基配列解析、 (Rで)マイクロアレイデータ解析中で利用するパッケージ、 プラスアルファのパッケージをインストールするやり方です。 Rパッケージの2大リポジトリであるCRANとBioconductor から提供されているパッケージ群のうち、一部のインストールに相当しますので、相当短時間でインストールが完了します。 SAFEではなくsafeパッケージの間違いでした。2015.04.24に修正済みです。ご指摘ありがとうございましたm(_ _)m limmaの取得先が間違ってCRANになっているのを2015.05.25に修正しました。
1. R本体を起動
2. CRANから提供されているパッケージ群のインストール
以下を「R コンソール画面上」でコピー&ペースト。 どこからダウンロードするか?と聞かれるので、その場合は自分のいる場所から近いサイトを指定しましょう。
#options(repos="http://cran.ism.ac.jp/")#利用するリポジトリを指定(統計数理研究所の場合) #(Rで)塩基配列解析で主に利用 install.packages("clValid") #Dunn's index計算用のパッケージ。2016.11.03追加 install.packages("openxlsx") #EXCELファイル(.xlsx)を直接読み込むためのパッケージ。2015.11.12追加 install.packages("PoissonSeq") install.packages("rbamtools") #BAM形式ファイルを直接読み込むためのパッケージ。2016.09.14追加 install.packages("samr") #(Rで)塩基配列解析でも利用 install.packages("seqinr") #(Rで)塩基配列解析でも利用 #(Rで)マイクロアレイデータ解析で利用 install.packages("cclust") install.packages("class") install.packages("e1071") install.packages("GeneCycle") install.packages("gptk") install.packages("GSA") install.packages("mixOmics") install.packages("pvclust") install.packages("RobLoxBioC") #2016.05.10追加 install.packages("som") install.packages("st") install.packages("varSelRF") #アグリバイオの他の講義科目で利用予定 install.packages("ape") install.packages("cluster") install.packages("fields") install.packages("KernSmooth") install.packages("mapdata") install.packages("maps") install.packages("MASS") install.packages("MVA") install.packages("RCurl") #2015.07.24追加 install.packages("rgl") install.packages("scatterplot3d")
3. Bioconductorから提供されているパッケージ群のインストール
ゲノム配列パッケージ以外です。
source("http://bioconductor.org/biocLite.R")#おまじない
#(Rで)塩基配列解析で主に利用
biocLite("baySeq", suppressUpdates=TRUE)
biocLite("biomaRt", suppressUpdates=TRUE)#(Rで)塩基配列解析でも利用
biocLite("Biostrings", suppressUpdates=TRUE)#(Rで)塩基配列解析でも利用
#biocLite("BiSeq", suppressUpdates=TRUE)#2016.07.06にコメントアウト(cosmoとdoMCがなくなったようです)
biocLite("BSgenome", suppressUpdates=TRUE)
biocLite("bsseq", suppressUpdates=TRUE)
biocLite("ChIPpeakAnno", suppressUpdates=TRUE)
biocLite("chipseq", suppressUpdates=TRUE)
biocLite("ChIPseqR", suppressUpdates=TRUE)
biocLite("ChIPsim", suppressUpdates=TRUE)
biocLite("cosmo", suppressUpdates=TRUE)
biocLite("CSAR", suppressUpdates=TRUE)
biocLite("DECIPHER", suppressUpdates=TRUE)#2016.12.29追加
biocLite("DEGseq", suppressUpdates=TRUE)
biocLite("DESeq", suppressUpdates=TRUE)
biocLite("DESeq2", suppressUpdates=TRUE)
biocLite("DiffBind", suppressUpdates=TRUE)
biocLite("doMC", suppressUpdates=TRUE)
biocLite("EBSeq", suppressUpdates=TRUE)
biocLite("EDASeq", suppressUpdates=TRUE)
biocLite("edgeR", suppressUpdates=TRUE)
biocLite("GenomicAlignments", suppressUpdates=TRUE)
biocLite("GenomicFeatures", suppressUpdates=TRUE)
biocLite("ggplot2", suppressUpdates=TRUE)
biocLite("girafe", suppressUpdates=TRUE)
biocLite("Heatplus", suppressUpdates=TRUE)#2015.11.12追加
biocLite("impute", suppressUpdates=TRUE)
biocLite("limma", suppressUpdates=TRUE)#(Rで)塩基配列解析でも利用
biocLite("maSigPro", suppressUpdates=TRUE)#(Rで)塩基配列解析でも利用
biocLite("MBCluster.Seq", suppressUpdates=TRUE)
biocLite("msa", suppressUpdates=TRUE) #2015.12.18追加
biocLite("htSeqTools", suppressUpdates=TRUE)
biocLite("NBPSeq", suppressUpdates=TRUE)
biocLite("phyloseq", suppressUpdates=TRUE)
biocLite("PICS", suppressUpdates=TRUE)
biocLite("qrqc", suppressUpdates=TRUE)
biocLite("QuasR", suppressUpdates=TRUE)
biocLite("r3Cseq", suppressUpdates=TRUE)
biocLite("REDseq", suppressUpdates=TRUE)
biocLite("rGADEM", suppressUpdates=TRUE)
biocLite("rMAT", suppressUpdates=TRUE)
biocLite("Rsamtools", suppressUpdates=TRUE)
biocLite("rtracklayer", suppressUpdates=TRUE)
biocLite("segmentSeq", suppressUpdates=TRUE)
biocLite("SeqGSEA", suppressUpdates=TRUE)
biocLite("seqLogo", suppressUpdates=TRUE)
biocLite("ShortRead", suppressUpdates=TRUE)
biocLite("SplicingGraphs", suppressUpdates=TRUE)
biocLite("SRAdb", suppressUpdates=TRUE)
biocLite("TCC", suppressUpdates=TRUE) #(Rで)塩基配列解析でも利用
biocLite("TxDb.Celegans.UCSC.ce6.ensGene", suppressUpdates=TRUE)
biocLite("TxDb.Hsapiens.UCSC.hg19.knownGene", suppressUpdates=TRUE)
biocLite("TxDb.Hsapiens.UCSC.hg38.knownGene", suppressUpdates=TRUE)
biocLite("TxDb.Mmusculus.UCSC.mm10.knownGene", suppressUpdates=TRUE)
biocLite("TxDb.Rnorvegicus.UCSC.rn5.refGene", suppressUpdates=TRUE)
#biocLite("yeastRNASeq", suppressUpdates=TRUE)
#(Rで)マイクロアレイデータ解析で利用
biocLite("affy", suppressUpdates=TRUE)
biocLite("agilp", suppressUpdates=TRUE)
biocLite("annotate", suppressUpdates=TRUE)
biocLite("ArrayExpress", suppressUpdates=TRUE)
biocLite("beadarray", suppressUpdates=TRUE)
biocLite("BeadDataPackR", suppressUpdates=TRUE)
biocLite("betr", suppressUpdates=TRUE)
biocLite("BHC", suppressUpdates=TRUE)
biocLite("Category", suppressUpdates=TRUE)
biocLite("clusterStab", suppressUpdates=TRUE)
biocLite("DNAcopy", suppressUpdates=TRUE)
biocLite("frma", suppressUpdates=TRUE)
biocLite("gage", suppressUpdates=TRUE)
biocLite("gcrma", suppressUpdates=TRUE)
biocLite("genefilter", suppressUpdates=TRUE)
biocLite("GEOquery", suppressUpdates=TRUE)
biocLite("GLAD", suppressUpdates=TRUE)
biocLite("globaltest", suppressUpdates=TRUE)
biocLite("golubEsets", suppressUpdates=TRUE)
biocLite("GSAR", suppressUpdates=TRUE) #2017.01.27追加
biocLite("GSEABase", suppressUpdates=TRUE)
biocLite("GSVAdata", suppressUpdates=TRUE)#2017.03.07追加
biocLite("hgu133a.db", suppressUpdates=TRUE)
biocLite("hgu133plus2probe", suppressUpdates=TRUE)
biocLite("hgug4112a.db", suppressUpdates=TRUE)
biocLite("illuminaMousev2.db", suppressUpdates=TRUE)
biocLite("lumi", suppressUpdates=TRUE)
biocLite("marray", suppressUpdates=TRUE)
biocLite("inSilicoDb", suppressUpdates=TRUE)
biocLite("Mulcom", suppressUpdates=TRUE)
biocLite("multtest", suppressUpdates=TRUE)
biocLite("OCplus", suppressUpdates=TRUE)
biocLite("org.Hs.eg.db", suppressUpdates=TRUE)
biocLite("pathview", suppressUpdates=TRUE)#2016.07.06にPathviewをpathviewに変更
biocLite("pcot2", suppressUpdates=TRUE)
biocLite("pd.rat230.2", suppressUpdates=TRUE)#2017.02.24追加
biocLite("PGSEA", suppressUpdates=TRUE)
biocLite("plier", suppressUpdates=TRUE)
biocLite("puma", suppressUpdates=TRUE)
biocLite("RankProd", suppressUpdates=TRUE)
biocLite("rat2302.db", suppressUpdates=TRUE)
biocLite("rat2302probe", suppressUpdates=TRUE)
biocLite("safe", suppressUpdates=TRUE)
biocLite("SAGx", suppressUpdates=TRUE)
biocLite("sigPathway", suppressUpdates=TRUE)
biocLite("SpeCond", suppressUpdates=TRUE)
biocLite("SPIA", suppressUpdates=TRUE)
biocLite("topGO", suppressUpdates=TRUE)
biocLite("vsn", suppressUpdates=TRUE)
4. Bioconductorから提供されているパッケージ群のインストール
ゲノム配列パッケージです。一つ一つの容量が尋常でないため、 必要に応じてテキストエディタなどに予めコピペしておき、いらないゲノムパッケージを削除してからお使いください。
source("http://bioconductor.org/biocLite.R")#おまじない
biocLite("BSgenome.Athaliana.TAIR.TAIR9", suppressUpdates=TRUE)#シロイヌナズナゲノム
biocLite("BSgenome.Celegans.UCSC.ce6", suppressUpdates=TRUE)#線虫ゲノム
biocLite("BSgenome.Drerio.UCSC.danRer7", suppressUpdates=TRUE)#ゼブラフィッシュゲノム
biocLite("BSgenome.Hsapiens.NCBI.GRCh38", suppressUpdates=TRUE)#ヒトゲノム(GRCh38)
biocLite("BSgenome.Hsapiens.UCSC.hg19", suppressUpdates=TRUE)#ヒトゲノム(hg19)
biocLite("BSgenome.Mmusculus.UCSC.mm10", suppressUpdates=TRUE)#マウスゲノム(mm10)
インストール | Rパッケージ | 必要最小限(数GB?!)
(Rで)マイクロアレイデータ解析中で利用するパッケージのみインストールするやり方です。 Rパッケージの2大リポジトリであるCRANとBioconductor から提供されているパッケージ群のうち、ごく一部のインストールに相当しますので、相当短時間でインストールが完了します。 SAFEではなくsafeパッケージの間違いでした。2015.04.24に修正済みです。ご指摘ありがとうございましたm(_ _)m limmaの取得先が間違ってCRANになっているのを2015.05.25に修正しました。
1. R本体を起動
2. CRANから提供されているパッケージ群のインストール
以下を「R コンソール画面上」でコピー&ペースト。 どこからダウンロードするか?と聞かれるので、その場合は自分のいる場所から近いサイトを指定しましょう。
install.packages("cclust")
install.packages("class")
install.packages("e1071")
install.packages("GeneCycle")
install.packages("gptk")
install.packages("GSA")
install.packages("mixOmics")
install.packages("pvclust")
#install.packages("RobLoxBioC")
install.packages("samr")
install.packages("seqinr")
install.packages("som")
install.packages("st")
install.packages("varSelRF")
3. Bioconductorから提供されているパッケージ群のインストール
ゲノム配列パッケージ以外です。
source("http://bioconductor.org/biocLite.R")#おまじない
biocLite("affy", suppressUpdates=TRUE)
biocLite("agilp", suppressUpdates=TRUE)
biocLite("annotate", suppressUpdates=TRUE)
biocLite("ArrayExpress", suppressUpdates=TRUE)
biocLite("beadarray", suppressUpdates=TRUE)
biocLite("BeadDataPackR", suppressUpdates=TRUE)
biocLite("betr", suppressUpdates=TRUE)
biocLite("BHC", suppressUpdates=TRUE)
biocLite("biomaRt", suppressUpdates=TRUE)
biocLite("Biostrings", suppressUpdates=TRUE)
biocLite("Category", suppressUpdates=TRUE)
biocLite("clusterStab", suppressUpdates=TRUE)
biocLite("DNAcopy", suppressUpdates=TRUE)
biocLite("frma", suppressUpdates=TRUE)
biocLite("gage", suppressUpdates=TRUE)
biocLite("gcrma", suppressUpdates=TRUE)
biocLite("genefilter", suppressUpdates=TRUE)
biocLite("GEOquery", suppressUpdates=TRUE)
biocLite("GLAD", suppressUpdates=TRUE)
biocLite("globaltest", suppressUpdates=TRUE)
biocLite("golubEsets", suppressUpdates=TRUE)
biocLite("GSEABase", suppressUpdates=TRUE)
biocLite("hgu133a.db", suppressUpdates=TRUE)
biocLite("hgu133plus2probe", suppressUpdates=TRUE)
biocLite("hgug4112a.db", suppressUpdates=TRUE)
biocLite("illuminaMousev2.db", suppressUpdates=TRUE)
biocLite("limma", suppressUpdates=TRUE)
biocLite("lumi", suppressUpdates=TRUE)
biocLite("marray", suppressUpdates=TRUE)
biocLite("maSigPro", suppressUpdates=TRUE)
biocLite("inSilicoDb", suppressUpdates=TRUE)
biocLite("Mulcom", suppressUpdates=TRUE)
biocLite("multtest", suppressUpdates=TRUE)
biocLite("OCplus", suppressUpdates=TRUE)
biocLite("org.Hs.eg.db", suppressUpdates=TRUE)
biocLite("Pathview", suppressUpdates=TRUE)
biocLite("pcot2", suppressUpdates=TRUE)
biocLite("PGSEA", suppressUpdates=TRUE)
biocLite("plier", suppressUpdates=TRUE)
biocLite("puma", suppressUpdates=TRUE)
biocLite("RankProd", suppressUpdates=TRUE)
biocLite("rat2302.db", suppressUpdates=TRUE)
biocLite("rat2302probe", suppressUpdates=TRUE)
biocLite("safe", suppressUpdates=TRUE)
biocLite("SAGx", suppressUpdates=TRUE)
biocLite("sigPathway", suppressUpdates=TRUE)
biocLite("SpeCond", suppressUpdates=TRUE)
biocLite("SPIA", suppressUpdates=TRUE)
biocLite("TCC", suppressUpdates=TRUE)
biocLite("topGO", suppressUpdates=TRUE)
biocLite("vsn", suppressUpdates=TRUE)
インストール | Rパッケージ | 個別
多くのBSgenome系パッケージや TxDb系のパッケージは、「ほぼ全て」の手順ではインストールされません。 理由は、BSgenomeはゲノム配列情報のパッケージなので、ヒトゲノムの様々なバージョン、マウスゲノム、ラットゲノムなどを全部入れると大変なことになるからです。 それでもピンポイントで必要に迫られる局面もあると思いますので、ここではRのパッケージを個別にインストールするやり方を示します。
1. ゼブラフィッシュゲノムのパッケージ(BSgenome.Drerio.UCSC.danRer7)をインストールしたい場合:
400MB程度あります...。
param <- "BSgenome.Drerio.UCSC.danRer7"#パッケージ名を指定 #本番 source("http://bioconductor.org/biocLite.R")#おまじない biocLite(param, suppressUpdates=TRUE) #おまじない
2. TxDb.Rnorvegicus.UCSC.rn5.refGeneパッケージのインストールをしたい場合:
param <- "TxDb.Rnorvegicus.UCSC.rn5.refGene"#パッケージ名を指定 #本番 source("http://bioconductor.org/biocLite.R")#おまじない biocLite(param, suppressUpdates=TRUE) #おまじない
3. TxDb.Hsapiens.UCSC.hg38.knownGeneパッケージのインストールをしたい場合:
param <- "TxDb.Hsapiens.UCSC.hg38.knownGene"#パッケージ名を指定 #本番 source("http://bioconductor.org/biocLite.R")#おまじない biocLite(param, suppressUpdates=TRUE) #おまじない
4. 線虫ゲノムのパッケージ(BSgenome.Celegans.UCSC.ce6)をインストールしたい場合:
20MB程度です。
param <- "BSgenome.Celegans.UCSC.ce6" #パッケージ名を指定 #本番 source("http://bioconductor.org/biocLite.R")#おまじない biocLite(param, suppressUpdates=TRUE) #おまじない
5. TxDb.Celegans.UCSC.ce6.ensGeneパッケージのインストールをしたい場合:
param <- "TxDb.Celegans.UCSC.ce6.ensGene"#パッケージ名を指定 #本番 source("http://bioconductor.org/biocLite.R")#おまじない biocLite(param, suppressUpdates=TRUE) #おまじない
6. Heatplusパッケージのインストールをしたい場合:
param <- "Heatplus" #パッケージ名を指定 #本番 source("http://bioconductor.org/biocLite.R")#おまじない biocLite(param, suppressUpdates=TRUE) #おまじない
(削除予定)Rのインストールと起動
よく分からない人でWindowsユーザーの方は以下を参考にしてください。2014年4月22日に作成したWindows用のインストール手順はこちら。 2014年5月14日にアップデートしたMac版のインストール手順こちら(by 孫建強氏)もあります。 注意点は、「Mac OS X のバージョンに関わらず R-3.1.0-snowleopard.pkg をインストールしたほうがよい」です。
1. Windows release版のインストールの場合:
- Rのインストーラを「実行」
- 聞かれるがままに「次へ」などを押してとにかくインストールを完了させる
- Windows Vistaの人は(パッケージのインストール中に書き込み権限に関するエラーが出るのを避けるために)「コントロールパネル」−「ユーザーアカウント」−「ユーザーアカウント制御の有効化または無効化」で、「ユーザーアカウント制御(UAC)を使ってコンピュータの保護に役立たせる」のチェックをあらかじめ外しておくことを強くお勧めします。
- インストールが無事完了したら、デスクトップに出現する「R3.X.Y (32 bitの場合; XやY中の数値はバージョンによって異なります)」または「R x64 3.X.Y (64 bitの場合)」アイコンをダブルクリックして起動
- 以下を、「R コンソール画面上」でコピー&ペーストする。10GB程度のディスク容量を要しますが一番お手軽です。(どこからダウンロードするか?と聞かれるので、その場合は自分のいる場所から近いサイトを指定)
source("http://www.iu.a.u-tokyo.ac.jp/~kadota/R/mvo.R")#おまじない install.packages(available.packages()[,1], dependencies=TRUE)#CRAN中にある全てのパッケージをインストール source("http://www.bioconductor.org/biocLite.R")#おまじない biocLite(all_group()) #Bioconductor中にある全てのパッケージをインストール - 「コントロールパネル」−「フォルダオプション」−「表示(タブ)」−「詳細設定」のところで、「登録されている拡張子は表示しない」のチェックを外してください。
2. Windows devel版(R-devel)のインストールの場合(advanced userのみ):
- Rのインストーラを「実行」
- 聞かれるがままに「次へ」などを押してとにかくインストールを完了させる
- R-develを起動し、以下を、「R コンソール画面上」でコピー&ペーストする。
for (i in available.packages()[,1]){#CRAN中にある全てのパッケージをインストール try(install.packages(i, dependencies=TRUE))#CRAN中にある全てのパッケージをインストール } #CRAN中にある全てのパッケージをインストール source("http://www.bioconductor.org/biocLite.R")#おまじない biocLite(all_group()) #Bioconductor中にある全てのパッケージをインストール
(削除予定)Rの昔のバージョンのインストール
DFW (Chen et al., Bioinformatics, 2007)というAffymetrixチップの正規化法でわりとよく "思い通りの"階層的クラスタリング結果を導くような遺伝子発現行列データを生成してくれるAffymetrixデータ用の正規化法(嫌味ではなくいい方法なんだと思います)があります。 しかしこの正規化法は、R2.7.2あたりだと正常に動作していましたが、比較的最近のバージョン(R2.8.1以降)ではうまく動いてくれません。 そのような場合でも、Rの昔のバージョンをインストールしてDFWを実行することによって、DFWを利用することができます。 このような目的のために、ここでは、Rの任意の昔のバージョンをインストールするやり方をR2.7.2のインストールを例に紹介します
- ここをクリックして、任意のRのバージョンのところをクリック(例えば2.7.2)
- R-X.Y.Z-win32.exe(例えばR-2.7.2-win32.exe)をクリックして「実行」ボタンなどを聞かれるがままに押す
- R-X.Y.Zのアイコンがデスクトップにできるので、立ち上げて以下をコピペ
source("http://bioconductor.org/biocLite.R")#おまじない biocLite("affy") #おまじない
これであとはDFWを参考にしてDFWの結果をエンジョイしてください。
使用例(初心者向け):
Step 1:
Rを起動して以下をコピー&ペーストしてみてください。自分のマイクロアレイデータ解析を実際にRを用いて行う上で、このページの情報をもとに自分がどのような作業をすれば目的を達成できるかの参考になるはずです。
1+2 #1+2を計算 hoge <- 4 #hogeに4を代入 hoge #hogeの中身を表示 sqrt(hoge) #4のルートを計算 sqrt(4) #4のルートを計算(当然同じ意味) #の後の文章はコメントなので何を書いてもいいですよ。
Step 2:
実際に自分のマイクロアレイデータを用いて解析をしようと思い始めたとき、数行を一度にコピー&ペーストすると、様々なパラメータを変更することができずにつまづくことがあるかもしれません。そのような場合、例えば「ワードパッド」や「メモ帳」で予め作成しておいた一連のコマンド群からなるrun.txtを用意しておき、その中身をコピー&ペーストすることでrun.txtの中身を実行します。
Step 3:
コマンドライン上に表示される R の出力をファイルにそのまま保存したいと思う場面が出てきます。このような場合、
- まず出力される先のディレクトリを、「ファイル」−「ディレクトリの変更」で指定
- 以下をコピー&ペースト
sink("out.txt") #出力ファイル名をout.txtとする 1+2 #1+2を計算 hoge <- 4 #hogeに4を代入 hoge #hogeの中身を表示 sqrt(hoge) #4のルートを計算 sqrt(4) #4のルートを計算(当然同じ意味) #の後の文章はコメントなので何を書いてもいいですよ。コマンドライン上に結果が表示されず、out.txtに結果が以下のように表示されていることと思います:
| out.txtの中身 |
[1] 3 [1] 4 [1] 2 [1] 2
尚、sink()と入力すれば、out.txtに出力させるのをやめさせることができます。
- library():どのようなパッケージがインストールされているかを知る
- library(help="パッケージ名"):「パッケージ名」で指定したパッケージ中にどのような関数があるかを知る
- update.packages():手持ちのパッケージをアップデート
- getBioC("パッケージ名"):「パッケージ名」で指定したパッケージをインストール
- sample(x, n, replace=F):ベクトルxから長さnの部分ベクトルをランダムにサンプリング
- objects():今現在利用可能なオブジェクのリストを表示
- unique():重複を除去
- duplicated():重複があるものをTRUEとして表示
- rle():例えば「x <- c("C", "A", "B", "C", "C", "D"); rle(sort(x))」とやると、Aが1, Bが1, Cが3, Dが1といった情報を返してくれる
- table():例えばある離散データ「x <- rpois(50, lambda = 4)」を生成させて、「table(factor(x, 0:max(x)))」とやると、どの数値のものがいくつあったかを返してくれる
サンプルデータ
-
3051 genes×38 samplesからなる二群の遺伝子発現データ。最初の27サンプルがG1群、残りの11サンプルがG2群のデータです。
sample1.txt (遺伝子発現データ)
sample1_cl.txt (クラスラベルデータ)
以下を実行して得られるデータと本質的に同じものです。
library(multtest) data(golub) dim(golub) -
6 genes×11 samplesからなる二群の遺伝子発現データ。最初の6サンプルがG1群、残りの5サンプルがG2群のデータです。
sample2.txt (遺伝子発現データ)
sample2_cl.txt (クラスラベルデータ)
-
45 genes×10 samplesからなる遺伝子発現データ。sample3.txt
このデータは以下のコマンドを実行したのち、sample3_tmp.txtのラベル情報部分を微修正して得ました。
sample3_tmp <- rbind(matrix(rnorm(150, mean=0, sd=0.2), ncol=10), matrix(rnorm(150, mean=1, sd=0.2), ncol=10), matrix(rnorm(150, mean=2, sd=0.2), ncol=10)) write.table(sample3_tmp, "sample3_tmp.txt", sep = "\t", append=F, quote=F, col.names=F) -
Ge et al., Genomics, 2005 (GSE2361)の22,283 genes×36 samplesからなる多群の遺伝子発現データ
GDS1096.txt
実際には
で読み込んでも「IDENTIFIER」カラムが余分にあります。そのため、読み込み後にGDS1096 <- read.table("GDS1096.txt", header=TRUE, row.names=1, sep="\t", quote="")
とやっておく必要があります。GDS1096$IDENTIFIER <- NULL
ちなみにこのデータはGDS1096からダウンロードして得られたGDS1096.soft.txtファイルを加工したものです。
MAS-quantified dataです(2007/7/3追加)。 -
Ge et al., Genomics, 2005 (GSE2361)の22,283 probesets×36 samplesからなる多群の遺伝子発現データ
RMA-preprocessed dataです。
sample5.txt -
10 genes×20 samplesからなる遺伝子発現データ。欠損値, NaN, NAなどを含むデータです。
sample6.txt -
Golub et al., Science, 1999の7,129 genesからなる二群の遺伝子発現データ
ALL(G1群; 47 samples)が1, AML(G2群; 25 samples)が2でラベルされています。
sample7.txt (遺伝子発現データ)
sample7_cl.txt (クラスラベルデータ)
out_f1 <- "sample7.txt" #出力ファイル名を指定してout_f1に格納 out_f2 <- "sample7_cl.txt" #出力ファイル名を指定してout_f2に格納 library(golubEsets) data(Golub_Merge) tmp_names <- paste(as.character(Golub_Merge$ALL.AML), colnames(exprs(Golub_Merge)), sep="_") data <- exprs(Golub_Merge) colnames(data) <- tmp_names tmp <- cbind(rownames(data), data) write.table(tmp, out_f1, sep = "\t", append=F, quote=F, row.names=F) data.cl <- as.numeric(Golub_Merge$ALL.AML) write.table(cbind(tmp_names, data.cl), out_f2, sep = "\t", append=F, quote=F, row.names=F, col.names=F)
-
Singh et al., Cancer Cell, 2002の12,600 genesからなる二群の遺伝子発現データ
最初の50サンプルがG1群(non-tumor prostate)、残りの52サンプルがG2群(prostate tumor)のデータです。
data_Singh_RMA.txt (RMA-quantified data; Jeffery et al., BMC Bioinformatics, 2006で公開されているSingh.txtを加工したもの)
data_Singh_MAS.txt (MAS-quantified data; 原著論文のweb supplementから利用可能なProstate_TN_final0701_allmeanScale.resを加工したもの)
「Prostate_TN_final0701_allmeanScale.res」中には12,600 clones分の情報しかないため、(ProbeSetIDが"1600***"という)余分な25 clones分のデータを除去している。
-
Singh et al., Cancer Cell, 2002の3,274 genesからなる二群の遺伝子発現データ
最初の50サンプルがG1群(non-tumor prostate)、残りの52サンプルがG2群(prostate tumor)のデータです。
data_Singh_RMA_3274.txt (RMA-quantified data)
data_Singh_MAS_3274.txt (MAS-quantified data)
計算を軽くするために、MASのデータで全102サンプル中半分(51サンプル)以上で"Present" callとなっていた3,274クローンからなるサブセットにしたものです。
- 1,000 genesからなる時系列の遺伝子発現データ maSigPro (Conesa et al., Bioinformatics, 2006) で提供されているサンプルデータです。
-
「通常状態(Control)のサンプルの薬剤処理後3時間(3 replicates), 9時間(2 replicates), そして27時間後(3 replicates)の遺伝子発現データ」、「低温状態(Cold)の...」、「高温状態(Heat)の...」からなる計1,000 ProbeSets×24 arraysからなる遺伝子発現データとその実験デザイン情報のデータ
sample10_3groups.txt (遺伝子発現データ)
sample10_3groups_cl.txt (実験デザイン情報データ) -
「通常状態(Control)のサンプルの薬剤処理後3時間(3 replicates), 9時間(2 replicates), そして27時間後(3 replicates)の遺伝子発現データ」、「低温状態(Cold)の...」からなる計1,000 ProbeSets×16 arraysからなる遺伝子発現データとその実験デザイン情報のデータ
sample10_2groups.txt (遺伝子発現データ)
sample10_2groups_cl.txt (実験デザイン情報データ) -
「ある(Control)のサンプルの薬剤処理後3時間(3 replicates), 9時間(2 replicates), そして27時間後(3 replicates)の遺伝子発現データ」からなる計1,000 ProbeSets×8 arraysからなる遺伝子発現データとその実験デザイン情報のデータ
sample10_1group.txt (遺伝子発現データ)
sample10_1group_cl.txt (実験デザイン情報データ) -
1,000 genesの時系列遺伝子発現データ
-
「サンプル1の薬剤処理後0.5, 2, 5, 12.3, 24時間後の遺伝子発現データ」と「サンプル2の薬剤処理後0.5, 2, 5, 12.3, 24時間後の遺伝子発現データ」からなる計1,000 ProbeSets×10 arraysからなる”対応あり”遺伝子発現データ
sample11_2groups_paired.txt (遺伝子発現データ)
sample11_2groups_paired_cl.txt (クラスラベルデータ) -
「サンプル1の薬剤処理後0.5, 2, 5, 12.3, 24時間後の遺伝子発現データ」と「サンプル2の薬剤処理後1.3, 4, 8, 12, 20時間後の遺伝子発現データ」からなる計1,000 ProbeSets×10 arraysからなる”対応なし”遺伝子発現データ
sample11_2groups_unpaired.txt (遺伝子発現データ)
sample11_2groups_unpaired_cl.txt (クラスラベルデータ) -
「サンプル1の薬剤処理後0.5, 2, 5, 12.3, 24時間後の遺伝子発現データ」からなる計1,000 ProbeSets×5 arraysからなる遺伝子発現データ
sample11_1group.txt (遺伝子発現データ)
sample11_1group_cl.txt (クラスラベルデータ)
-
「サンプル1の薬剤処理後0.5, 2, 5, 12.3, 24時間後の遺伝子発現データ」と「サンプル2の薬剤処理後0.5, 2, 5, 12.3, 24時間後の遺伝子発現データ」からなる計1,000 ProbeSets×10 arraysからなる”対応あり”遺伝子発現データ
-
Laub et al., Science, 2000の1,444 genes×11 time points (0, 15, 30, 45, 60, 75, 90, 105, 120, 135, 150min)からなる時系列遺伝子発現データ
sample12.txt
このデータは以下のコマンドを実行したのち、sample12_tmp.txtのラベル情報部分を微修正して得ました。
library(GeneCycle) data(caulobacter) data <- t(caulobacter) tmp <- cbind(rownames(data), data) write.table(tmp, "sample12_tmp.txt", sep = "\t", append=F, quote=F, row.names=F)
-
Hayashi et al., Psychother Psychosom, 2006 (GSE1322)の22,575 genesからなる二群の遺伝子発現データ(Agilent two-colorデータ)
-
最初の14サンプルがG1群(面白い話を聞いた患者)、残りの7サンプルがG2群(退屈な講義を聞いた患者)でlog2(聞いた後/聞く前)の値になっています。
sample13.txt -
sample13.txtのサブセットで、最初の7サンプルがG1群(面白い話を聞いた患者)、残りの7サンプルがG2群(退屈な講義を聞いた患者)でlog2(聞いた後/聞く前)の値になっています。原著論文ではこのサブセットで解析していたので念のため用意しました。
sample13_7vs7.txt
このデータはsample13.txtを入力として、以下のコマンドを実行することによって得ました。
in_f <- "sample13.txt" #入力ファイル名を指定してin_fに格納 out_f <- "sample13_7vs7.txt" #出力ファイル名を指定してout_fに格納 #データファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 data.tmp <- data[,c(3:6,9,13:21)] #行列dataの中から3-6, 9, 13-21列のデータのみ抽出してdata.tmpに格納 #ファイルに保存 tmp <- cbind(rownames(data), data.tmp) #遺伝子名の右側にdata.tmpを追加して、tmpに格納。 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
-
最初の14サンプルがG1群(面白い話を聞いた患者)、残りの7サンプルがG2群(退屈な講義を聞いた患者)でlog2(聞いた後/聞く前)の値になっています。
-
22,283 genes×6 samplesからなる二群の遺伝子発現データ。最初の3サンプルがG1群、残りの3サンプルがG2群のデータです。
sample14.txt -
5 genes×8 samplesからなる多群の遺伝子発現データ。
以下のクラスラベルデータは"tissue4"特異的高発現遺伝子を検出したいときのものです。
sample15.txt (遺伝子発現データ)
sample15_cl.txt (クラスラベルデータ) -
3 genes×11 samplesからなる二群の遺伝子発現データ。
最初の6サンプルがG1群、残りの5サンプルがG2群のデータです。2014年5月23にサンプルラベル情報を「A1, A2, ..., B1, B2, ...」から 「G1_1, G1_2, ..., G2_1, G2_2, ...」に変更しました。
sample16.txt (遺伝子発現データ; 対数変換前)
sample16_cl.txt (クラスラベルデータ)
sample16_log.txt (遺伝子発現データ; 対数変換後)
対数変換後のデータは以下のコピペで作成しました。
in_f <- "sample16.txt" #入力ファイル名を指定してin_fに格納 out_f <- "sample16_log.txt" #出力ファイル名を指定してout_fに格納 #データファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 summary(data) #シグナル強度の分布を確認し、ダイナミックレンジが4桁程度あることを確認 data[data < 1] <- 1 #シグナル強度が1未満のものを1にする data.log <- log(data, base=2) #log2-transformed dataをdata.logに格納 summary(data.log) #対数変換後のシグナル強度の分布を確認 #ファイルに保存 tmp <- cbind(rownames(data), data.log) #遺伝子名の右側にdata.logを追加して、tmpに格納。 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
-
14,026 genes×8 samplesからなる二群の遺伝子発現データ)。
最初の4サンプルがG1群、残りの4サンプルがG2群のデータです。
対数変換していないデータ:sample17_unlog.txt
対数変換しているデータ:sample17.txt
-
以下の図のようなデータ
sample18_5vs5.txt

-
10 genesからなる遺伝子発現データ。RMA法を適用したときにサンプル数の増減による影響を調べるためのデータです。
2 samplesからなるデータ:sample19.txt
3 samplesからなるデータ:sample19_plus1.txt
-
Nakai et al., BBB, 2008のGSE7623由来データ(RMA-preprocessed)
- data_GSE7623_rma.txt(31,099 probesets×24 samples)
- data_mas.txt(31,099 probesets×24 samples; ラベル情報部分をわかりやすくしたもの)
- data_rma_2.txt(31,099 probesets×24 samples; ラベル情報部分をわかりやすくしたもの)
- data_rma_2_BAT.txt(31,099 probesets×8 samples; BAT sampleのみでfed vs. 24h-fastedの2群間比較用)
- data_rma_2_LIV.txt(31,099 probesets×8 samples; LIV sampleのみでfed vs. 24h-fastedの2群間比較用)
- data_rma_2_WAT.txt(31,099 probesets×8 samples; WAT sampleのみでfed vs. 24h-fastedの2群間比較用)
GSM184414-184417: Brown adipose tissue (BAT), fed GSM184418-184421: Brown adipose tissue (BAT), 24 h-fasted GSM184422-184425: White adipose tissue (WAT), fed GSM184426-184429: White adipose tissue (WAT), 24 h-fasted GSM184430-184433: Liver tissue (LIV), fed GSM184434-184437: Liver tissue (LIV), 24 h-fasted
- data_rma_2_nr.txt(14,132 genes×24 samples; 同じgene symbolのものをまとめたもの)
- data_rma_2_nr_BAT.txt(14,132 genes×8 samples; BAT sampleのみでfed vs. 24h-fastedの2群間比較用)
- data_rma_2_nr_LIV.txt(14,132 genes×8 samples; LIV sampleのみでfed vs. 24h-fastedの2群間比較用)
ちなみに、これは「Affymetrix Rat Genome 230 2.0 Array」を用いて取得したデータでGPL1355からアノテーションファイルを取得可能です。 2群間比較手法の一つであるRank products (Breitling_2004)の2をテンプレートとしてFDR < 0.05を満たすprobesetIDを得た結果ファイルが以下のものたち:
- data_rma_2_BAT.txtを入力として得られた発現変動遺伝子IDリストファイル:result_rankprod_BAT_id.txt
- data_rma_2_LIV.txtを入力として得られた発現変動遺伝子IDリストファイル:result_rankprod_LIV_id.txt
- data_rma_2_WAT.txtを入力として得られた発現変動遺伝子IDリストファイル:result_rankprod_WAT_id.txt
(Rで)塩基配列解析のイントロ | 一般 | 任意のキーワードを含む行を抽出(基礎)の11をテンプレートとしてprobesetID --> RefSeq IDに変換したファイルが以下のものたち:
- result_rankprod_BAT_RefSeq_DEG.txt(774 RefSeq IDs)
- result_rankprod_BAT_RefSeq_nonDEG.txt(12,969 RefSeq IDs)
- result_rankprod_LIV_RefSeq_DEG.txt(559 RefSeq IDs)
- result_rankprod_LIV_RefSeq_nonDEG.txt(13,255 RefSeq IDs)
- result_rankprod_WAT_RefSeq_DEG.txt(601 RefSeq IDs)
- result_rankprod_WAT_RefSeq_nonDEG.txt(13,269 RefSeq IDs)
(Rで)塩基配列解析の前処理 | フィルタリング | 任意のIDを含む配列を抽出 などをテンプレートとしてリスト中のRefSeq IDに相当する(ACGTのみからなる配列で配列長が同じ)サブセットを抽出したmulti-fastaファイル群:
- seq_BAT_DEG.fa(563 RefSeq sequences)
- seq_BAT_nonDEG.fa(8,898 RefSeq sequences)
- seq_LIV_DEG.fa(426 RefSeq sequences)
- seq_LIV_nonDEG.fa(9,075 RefSeq sequences)
- seq_WAT_DEG.fa(453 RefSeq sequences)
- seq_WAT_nonDEG.fa(9,092 RefSeq sequences)
-
TCCパッケージ(Sun et al., BMC Bioinformatics, 2013)中の8 genes×10 tissuessからなる発現データ(sample21.txt)です。
ROKU論文(Kadota et al., BMC Bioinformatics, 2006)のFig.1で示した仮想データに似た数値にしてあります。以下のコピペで作成しました:
library(TCC) #パッケージの読み込み data(hypoData_ts) #データをロード #ファイルに保存 tmp <- cbind(rownames(hypoData_ts), hypoData_ts)#「rownames情報」と「発現データ」を列方向で結合した結果をtmpに格納 write.table(tmp, "sample21.txt", sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
-
10000 genes×6 samplesからなる二群の遺伝子発現データ。
最初の3サンプルがG1群、残りの3サンプルがG2群の標準正規分布に従う乱数からなるシミュレーションデータです。
乱数を発生させただけのデータなので、発現変動遺伝子(DEG)がない全てがnon-DEGのデータです。
以下のコピペで作成しました:
out_f <- "sample22.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 3 #G1群のサンプル数を指定 param_G2 <- 3 #G2群のサンプル数を指定 param_Ngene <- 10000 #全遺伝子数を指定 #ランダムデータの生成 set.seed(1000) #おまじない(同じ乱数になるようにするため) hoge <- rnorm(param_Ngene*(param_G1+param_G2))#param_Ngene*(param_G1+param_G2)個分の乱数を発生させた結果をhogeに格納 data <- matrix(hoge, nrow=param_Ngene) #param_Ngene*(param_G1+param_G2)個分の要素からなるベクトルhogeを変換して(param_Ngene)個の行数からなる行列を作成した結果をdataに格納 rownames(data) <- paste("gene", 1:param_Ngene, sep="_")#行名を付与 colnames(data) <- c(paste("G1_rep",1:param_G1,sep=""),paste("G2_rep",1:param_G2,sep=""))#列名を付与 #ファイルに保存 tmp <- cbind(rownames(data), data) #「rownames情報」と「発現データ」を列方向で結合した結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
-
10,000 genes×6 samplesからなる二群の遺伝子発現データ。
最初の3サンプルがG1群、残りの3サンプルがG2群の標準正規分布に従う乱数からなるシミュレーションデータです。
乱数発生後に、さらに最初の10% 分についてG1群に相当するところのみ数値を+3している(つまり10% がG1群で高発現というシミュレーションデータを作成している)
以下のコピペで作成しました:
out_f <- "sample23.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 3 #G1群のサンプル数を指定 param_G2 <- 3 #G2群のサンプル数を指定 param_Ngene <- 10000 #全遺伝子数を指定 param_PDEG <- 0.1 #全遺伝子に占める発現変動遺伝子の割合(PDEG)を指定 #ランダムデータの生成 set.seed(1000) #おまじない(同じ乱数になるようにするため) hoge <- rnorm(param_Ngene*(param_G1+param_G2))#param_Ngene*(param_G1+param_G2)個分の乱数を発生させた結果をhogeに格納 data <- matrix(hoge, nrow=param_Ngene) #param_Ngene*(param_G1+param_G2)個分の要素からなるベクトルhogeを変換して(param_Ngene)個の行数からなる行列を作成した結果をdataに格納 rownames(data) <- paste("gene", 1:param_Ngene, sep="_")#行名を付与 colnames(data) <- c(paste("G1_rep",1:param_G1,sep=""),paste("G2_rep",1:param_G2,sep=""))#列名を付与 #最初の(param_Ngene*param_PDEG)行分についてG1群のデータを+3している head(data) #+3する前のデータの一部を表示させている data[1:(param_Ngene*param_PDEG),1:param_G1] <- data[1:(param_Ngene*param_PDEG),1:param_G1] + 3#+3を実行 head(data) #+3した後のデータの一部を表示させている #ファイルに保存 tmp <- cbind(rownames(data), data) #「rownames情報」と「発現データ」を列方向で結合した結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
-
Kamei et al., PLoS One, 2013のGSE30533データ(二群間比較用)
最初の5サンプルがG1(Fe_short)群、残りの5サンプルがG2(control)群です。
MAS5法適用後のデータ:data_GSE30533_mas.txt(31,099 probesets×10 samples)
RMA法適用後のデータ:data_GSE30533_rma.txt(31,099 probesets×10 samples)
rmx法適用後のデータ:data_GSE30533_rmx.txt(31,099 probesets×10 samples)
以下のコピペで作成しました:
out_f1 <- "data_GSE30533_mas.txt" #出力ファイル名を指定してout_f1に格納 out_f2 <- "data_GSE30533_rma.txt" #出力ファイル名を指定してout_f2に格納 out_f3 <- "data_GSE30533_rmx.txt" #出力ファイル名を指定してout_f3に格納 param <- "GSE30533" #入手したいIDを指定 #必要なパッケージをロード library(ArrayExpress) #パッケージの読み込み library(affy) #パッケージの読み込み library(RobLoxBioC) #パッケージの読み込み #前処理(データ取得) hoge <- ArrayExpress(param, save=F) #paramで指定したIDのCELファイルなどを取得した結果をhogeに格納 #本番(MAS5) eset <- mas5(hoge) #MASを実行し、結果をesetに保存 exprs(eset) <- log(exprs(eset), 2) #底を2として対数変換 data <- exprs(eset) #dataとして取り扱う colnames(data) <- c(paste("G1_", 1:5, sep=""), paste("G2_", 1:5, sep=""))#列名を付与 tmp <- cbind(rownames(data), data) #「rownames情報」と「発現データ」を列方向で結合した結果をtmpに格納 write.table(tmp, out_f1, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存 #本番(RMA) eset <- rma(hoge) #RMAを実行し、結果をesetに保存 data <- exprs(eset) #dataとして取り扱う colnames(data) <- c(paste("G1_", 1:5, sep=""), paste("G2_", 1:5, sep=""))#列名を付与 tmp <- cbind(rownames(data), data) #「rownames情報」と「発現データ」を列方向で結合した結果をtmpに格納 write.table(tmp, out_f2, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存 #本番(RMX) eset <- robloxbioc(hoge) #rmxを実行し、結果をesetに保存 exprs(eset) <- log(exprs(eset), 2) #底を2として対数変換 data <- exprs(eset) #dataとして取り扱う colnames(data) <- c(paste("G1_", 1:5, sep=""), paste("G2_", 1:5, sep=""))#列名を付与 tmp <- cbind(rownames(data), data) #「rownames情報」と「発現データ」を列方向で結合した結果をtmpに格納 write.table(tmp, out_f3, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
-
10,000 genes×9 samplesからなる3群の遺伝子発現データ。
最初の3サンプルがG1群、残りの3サンプルがG2群の標準正規分布に従う乱数からなるシミュレーションデータです。
乱数発生後に、(1)1-1000行分についてG1群に相当するところのみ数値を+3(つまり1000個がG1群で高発現)
(2)1001-2000行分についてG2群に相当するところのみ数値を+3(つまり1000個がG2群で高発現) (3)2001-3000行分についてG3群に相当するところのみ数値を+3(つまり1000個がG3群で高発現)以下のコピペで作成しました:
out_f <- "sample25.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 3 #G1群のサンプル数を指定 param_G2 <- 3 #G2群のサンプル数を指定 param_G3 <- 3 #G3群のサンプル数を指定 param_Ngene <- 10000 #全遺伝子数を指定 param_DEG_G1 <- 1:1000 #G1で高発現とする位置を指定 param_DEG_G2 <- 1001:2000 #G2で高発現とする位置を指定 param_DEG_G3 <- 2001:3000 #G3で高発現とする位置を指定 #ランダムデータの生成 data.cl <- c(rep(1, param_G1), rep(2, param_G2), rep(3, param_G3))#G1群を1、G2群を2、G3群を3としたベクトルdata.clを作成 set.seed(1000) #おまじない(同じ乱数になるようにするため) hoge <- rnorm(param_Ngene*length(data.cl))#param_Ngene*length(data.cl)個分の乱数を発生させた結果をhogeに格納 data <- matrix(hoge, nrow=param_Ngene) #ベクトルhogeを変換して(param_Ngene)個の行数からなる行列を作成した結果をdataに格納 rownames(data) <- paste("gene", 1:param_Ngene, sep="_")#行名を付与 colnames(data) <- c(paste("G1_rep",1:param_G1,sep=""), paste("G2_rep",1:param_G2,sep=""), paste("G3_rep",1:param_G3,sep=""))#列名を付与 #DEGを導入 data[param_DEG_G1, data.cl==1] <- data[param_DEG_G1, data.cl==1] + 3#param_DEG_G1行についてG1群のデータを+3 data[param_DEG_G2, data.cl==2] <- data[param_DEG_G2, data.cl==2] + 3#param_DEG_G2行についてG2群のデータを+3 data[param_DEG_G3, data.cl==3] <- data[param_DEG_G3, data.cl==3] + 3#param_DEG_G3行についてG3群のデータを+3 #ファイルに保存 tmp <- cbind(rownames(data), data) #保存したい情報をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
-
23 genes×6 samplesからなる仮想データ。
マイクロアレイデータの図で、高発現のものと低発現のものを疑似色(pseudo-color)で表現するヒートマップを作成するときに、 オプションの挙動を把握するために作成しました。
- GSARパッケージ (Rahmatallah et al., BMC Bioinformatics, 2017) 中で提供されているp53DataSetと同じ2群間比較用データ(17 wild-type samples vs. 33 mutant samples)。
out_f1 <- "sample10.txt" #出力ファイル名を指定してout_f1に格納 out_f2 <- "sample10_cl.txt" #出力ファイル名を指定してout_f2に格納 library(maSigPro) data(data.abiotic) data(edesign.abiotic) write.table(data.abiotic, out_f1, sep = "\t", append=F, quote=F, col.names=T) write.table(edesign.abiotic, out_f2, sep = "\t", append=F, quote=F, col.names=T)
8,655 genes×50 samplesのアレイデータ(sample27.txt; 約7.3MB)
以下のコピペで作成しました:
out_f <- "sample27.txt" #出力ファイル名を指定してout_fに格納 #必要なパッケージをロード library(GSAR) #パッケージの読み込み #発現データの呼び出し data(p53DataSet) #GSARパッケージ中のp53DataSetオブジェクトの呼び出し data <- p53DataSet #オブジェクト名の変更(dataとして取り扱う) #ファイルに保存 tmp <- cbind(rownames(data), data) #保存したい情報をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F, col.names=T)#tmpの中身を指定したファイル名で保存
イントロ | 発現データ取得 | 公共DBから
遺伝子発現(主にマイクロアレイ)データベースをリストアップします。
一次データベース
- GEO:Barrett et al., Nucleic Acids Res., 2013
- GSE7623(ラット24サンプル, 62MB):Nakai et al., BBB, 2008
- GSE30533(ラット10サンプル, 25MB):Kamei et al., PLoS One, 2013
- GSE2361(ヒト36サンプル, 130MB):Ge et al., Genomics, 2005
- GSE10246(マウス182サンプル, 1.1GB):Lattin et al., Immunome Res., 2008
- GSE1133(ヒトとマウス438サンプル, 1.7GB):Su et al., Proc Natl Acad Sci U S A, 2004
- GSE5364(ヒト341サンプル, 生データなし):Yu et al., PLoS Genet., 2008
- GSE15998(マウス106サンプル, 4.0GB):原著論文はなし?!エクソンアレイ
- ArrayExpress:Rustici et al., Nucleic Acids Res., 2013
- GSE7623(ラット24サンプル, 62MB):Nakai et al., BBB, 2008
- GSE30533(ラット10サンプル, 25MB):Kamei et al., PLoS One, 2013
- GSE2361(ヒト36サンプル, 130MB):Ge et al., Genomics, 2005
- GSE10246(マウス182サンプル, 1.1GB):Lattin et al., Immunome Res., 2008
- GSE1133(リンク先なし):Su et al., Proc Natl Acad Sci U S A, 2004
- GSE5364(ヒト341サンプル, 生データなし):Yu et al., PLoS Genet., 2008
- GSE15998(マウス106サンプル, 4.0GB):原著論文はなし?!エクソンアレイ
イントロ | 発現データ取得 | inSilicoDb(Taminau_2011)
inSilico Db (Coletta et al., Genome Biol., 2012) というヒト(マウス、ラット)のAffymetrixデータからなる二次DBがあります。 この中で提供されている?!GEO ID(基本は"GSE"のID)で取得可能なcurated datasetsを inSilicoDbというRパッケージで取得するやり方を示します。 しかし、運よく存在すればいいのですが、not availableになるケースが多いです。 運がよければfrozen RMA法(fRMA; McCall et al., Biostatistics, 2010)で正規化したデータなどを取得可能です。 2015年5月にgetDataset関数のオプション名がgenesからfeaturesに変わっていたので若干変更しました。 しかし、「 INSILICODB: Please login first to access this dataset. エラー: Stopped because of previous errors」というエラーメッセージが出てしまい、嫌になったので放置することにします。 2013年ごろはうまくうごいたのですがorz...
「ファイル」−「ディレクトリの変更」でファイルを保存したいディレクトリに移動し以下をコピペ。
1. AffymetrixデータGSE30533 (Kamei et al., PLoS One, 2013)のデータを取得したい場合:
2013年8月20日現在、15,923 probesetsになります。
param <- "GSE30533" #入手したいIDを指定 #必要なパッケージをロード library(inSilicoDb) #パッケージの読み込み #本番(データ取得) hoge <- getPlatforms(param) #アレイ(プラットフォーム)情報を取得 eset <- getDataset(param, hoge[[1]], norm="ORIGINAL", features="PROBE")#paramで指定したIDのsubmitterが登録した正規化後のデータ(norm="ORIGINAL")を取得 dim(exprs(eset)) #行数と列数を表示 head(exprs(eset)) #最初の数行を表示
2. AffymetrixデータGSE30533 (Kamei et al., PLoS One, 2013)のデータを取得したい場合:
2013年8月20日現在、以下をやっても"not available"となります。
param <- "GSE30533" #入手したいIDを指定 #必要なパッケージをロード library(inSilicoDb) #パッケージの読み込み #本番(データ取得) hoge <- getPlatforms(param) #アレイ(プラットフォーム)情報を取得 eset <- getDataset(param, hoge[[1]], norm="FRMA", features="PROBE")#paramで指定したIDのfRMA正規化後のデータを取得 dim(exprs(eset)) #行数と列数を表示
3. AffymetrixデータGSE30533 (Kamei et al., PLoS One, 2013)のデータを取得したい場合:
15,923 probeset IDsから10,397 gene symbolsになっていることがわかります。
param <- "GSE30533" #入手したいIDを指定 #必要なパッケージをロード library(inSilicoDb) #パッケージの読み込み #本番(データ取得) hoge <- getPlatforms(param) #アレイ(プラットフォーム)情報を取得 eset <- getDataset(param, hoge[[1]], norm="ORIGINAL", features="GENE")#paramで指定したIDのsubmitterが登録した正規化後のデータ(log2 RMA)を取得 dim(exprs(eset)) #行数と列数を表示 head(exprs(eset)) #最初の数行を表示
イントロ | 発現データ取得 | ArrayExpress(Kauffmann_2009)
マイクロアレイデータベースArrayExpress に登録されているデータをArrayExpressというRパッケージで取得するやり方を示します。 GEO IDでも検索可能であり、CELファイルデータも取得可能、任意のpreprocessing法を適用可能、 などの利点からこのパッケージ経由での利用をお勧めします。
「ファイル」−「ディレクトリの変更」でファイルを保存したいディレクトリに移動し以下をコピペ。
1. AffymetrixデータE-MEXP-1422 (Bourgon et al., PNAS, 2010)のCELファイルを取得し、RMA法(Irizarry et al., Biostatistics, 2003)を実行して得られた発現情報を取得したい場合:
以下のArrayExpress関数のオプションをsave=Fからsave=Tに変更すると、CELファイルなどを含む全データのダウンロードも同時に行ってくれます。 が、そんなことをいちいちやらなくてもReadAffy関数を用いて読み込んだ状態と同じなので直接RMA(Irizarry et al., Biostatistics, 2003)などの任意の正規化法を適用可能です。
out_f <- "data_rma.txt" #出力ファイル名を指定してout_fに格納 param <- "E-MEXP-1422" #入手したいIDを指定 #必要なパッケージをロード library(ArrayExpress) #パッケージの読み込み library(affy) #パッケージの読み込み #前処理(データ取得) hoge <- ArrayExpress(param, save=F) #paramで指定したIDのデータを取得した結果をhogeに格納 #本番 eset <- rma(hoge) #RMAを実行し、結果をesetに保存 #ファイルに保存 write.exprs(eset, file=out_f) #結果を指定したファイル名で保存
2. AffymetrixデータGSE30533 (Kamei et al., PLoS One, 2013)のCELファイルを取得したい場合:
GSE30533というID自体はGEOのものですが、比較的最近のデータ?!についてはGEOとArrayExpress間で共有しているようです。ちなみにArrayExpress内でのIDは"E-GEOD-30533"となっています。
param <- "GSE30533" #入手したいIDを指定 #必要なパッケージをロード library(ArrayExpress) #パッケージの読み込み #前処理(データ取得) hoge <- getAE(param, type="raw", extract=F)#paramで指定したIDの生データをダウンロード("extract=T"にすると圧縮ファイルを自動的に解凍してくれますが大量のファイル数になります...)
3. AffymetrixデータGSE7623 (Nakai et al., BBB, 2008)のCELファイルを取得したい場合:
param <- "GSE7623" #入手したいIDを指定 #必要なパッケージをロード library(ArrayExpress) #パッケージの読み込み #前処理(データ取得) hoge <- getAE(param, type="raw", extract=F)#paramで指定したIDの生データをダウンロード("extract=T"にすると圧縮ファイルを自動的に解凍してくれますが大量のファイル数になります...)
4. AgilentデータGSE7866 (Tesar et al., Nature, 2007)の生ファイルを取得したい場合:
生データファイルが存在しないので、adf, sdrf, and idf形式の計3ファイルしかダウンロードされない例です。
param <- "GSE7866" #入手したいIDを指定 #必要なパッケージをロード library(ArrayExpress) #パッケージの読み込み #前処理(データ取得) hoge <- getAE(param, type="raw", extract=F)#paramで指定したIDの生データをダウンロード("extract=T"にすると圧縮ファイルを自動的に解凍してくれますが大量のファイル数になります...)
5. AgilentデータGSE10417 (Chikahisa et al., Endocrinology, 2008)の生ファイルを取得したい場合:
GEOには存在するが、ArrayExpressからはGSE IDで取得できない例です。E-GEOD-10417で検索してもだめです。
param <- "GSE10417" #入手したいIDを指定 #必要なパッケージをロード library(ArrayExpress) #パッケージの読み込み #前処理(データ取得) hoge <- getAE(param, type="raw", extract=F)#paramで指定したIDの生データをダウンロード("extract=T"にすると圧縮ファイルを自動的に解凍してくれますが大量のファイル数になります...)
6. AffymetrixデータGSE781 (Lenburg et al., BMC Cancer, 2003)のCELファイルを取得したい場合:
GSE781は2種類のアレイ(GPL96 and GPL97)を使っています。ファイルサイズが大きい(全部で1GB程度?!)ので注意してください。
param <- "GSE781" #入手したいIDを指定 #必要なパッケージをロード library(ArrayExpress) #パッケージの読み込み #前処理(データ取得) hoge <- getAE(param, type="raw", extract=F)#paramで指定したIDの生データをダウンロード("extract=T"にすると圧縮ファイルを自動的に解凍してくれますが大量のファイル数になります...)
イントロ | 発現データ取得 | GEOquery (Davis_2007)
公共DBGene Expression Omnibus (GEO)に登録されているデータをGEOqueryというRパッケージを用いてゲットするやり方を示します。
が、このパッケージの利用はおすすめできません。理由は、発現データがどんな正規化法(RMAとやMBEIなど)で得られたものかや対数変換の有無などがそのIDのsubmitter依存(inconsistent preprocessing)だからです(Taminau et al., BMC Bioinformatics, 2012)。
「ファイル」−「ディレクトリの変更」でファイルを保存したいディレクトリに移動し以下をコピペ。
1. AffymetrixデータGSE7623 (Nakai et al., BBB, 2008)のプローブレベルデータファイル(.CEL)を入手したい場合:
param <- "GSE7623" #入手したいGEO IDを指定 #必要なパッケージをロード library(GEOquery) #パッケージの読み込み #本番 getGEOSuppFiles(param) #指定したGEO IDのサプリメントファイル(CELファイルに相当)をダウンロード
2. AffymetrixデータGSE7623 (Nakai et al., BBB, 2008)の発現情報を取得したい場合:
GSE7623は1種類のアレイ(GPL1355)しか使っていないので、1つのファイルのみ生成されます。
param1 <- "GSE7623" #入手したいGEO IDを指定 param2 <- "hoge2_" #出力ファイル名の最初の部分を指定 #必要なパッケージをロード library(GEOquery) #パッケージの読み込み #前処理 eset <- getGEO(param1) #指定したGEO IDのデータを取得した結果をesetに格納 sapply(eset, annotation) #用いられたアレイ情報(GPL ID)を表示 #本番 hoge <- sapply(eset, annotation) #用いられたアレイ情報(GPL ID)をhogeに格納 for(i in 1:length(hoge)){ #hogeの要素数(用いられたアレイ数)分だけループを回す out_f <- paste(param2, hoge[i], ".txt", sep="")#出力ファイル名を作成した結果をout_fに格納 write.exprs(eset[[i]], file=out_f) #outの中身を指定したファイル名で保存。 }
3. AffymetrixデータGSE781 (Lenburg et al., BMC Cancer, 2003)の発現情報を取得したい場合:
GSE781は2種類のアレイ(GPL96 and GPL97)を使っているので、2つのファイルが生成されます。
param1 <- "GSE781" #入手したいGEO IDを指定 param2 <- "hoge3_" #出力ファイル名の最初の部分を指定 #必要なパッケージをロード library(GEOquery) #パッケージの読み込み #前処理 eset <- getGEO(param1) #指定したGEO IDのデータを取得した結果をesetに格納 sapply(eset, annotation) #用いられたアレイ情報(GPL ID)を表示 #本番 hoge <- sapply(eset, annotation) #用いられたアレイ情報(GPL ID)をhogeに格納 for(i in 1:length(hoge)){ #hogeの要素数(用いられたアレイ数)分だけループを回す out_f <- paste(param2, hoge[i], ".txt", sep="")#出力ファイル名を作成した結果をout_fに格納 write.exprs(eset[[i]], file=out_f) #outの中身を指定したファイル名で保存。 }
4. two-color AgilentデータGSE1322 (Hayashi et al., Psychother. Psychosom., 2006)を入手したい場合:
詳細はGEOのGSE1322でわかりますが、ここで入手している発現データ
(全部糖尿病患者のperipheral bloodサンプル)はいわゆるlog ratioです。具体的にはlog2(Cy5/Cy3)で、
GSM21742: (面白い話を聞いた患者ID1)log2(After/Before) GSM21743: (面白い話を聞いた患者ID2)log2(After/Before) GSM21744: (面白い話を聞いた患者ID3)log2(After/Before) GSM21745: (面白い話を聞いた患者ID5)log2(After/Before) GSM21746: (面白い話を聞いた患者ID6)log2(After/Before) GSM21747: (面白い話を聞いた患者ID7)log2(After/Before) GSM21748: (面白い話を聞いた患者ID8)log2(After/Before) GSM21749: (面白い話を聞いた患者ID9)log2(After/Before) GSM21750: (面白い話を聞いた患者ID10)log2(After/Before) GSM21751: (面白い話を聞いた患者ID11)log2(After/Before) GSM21752: (面白い話を聞いた患者ID13)log2(After/Before) GSM21753: (面白い話を聞いた患者ID14)log2(After/Before) GSM21758: (面白い話を聞いた患者ID16)log2(After/Before) GSM21759: (面白い話を聞いた患者ID17)log2(After/Before) GSM21761: (退屈な講義を聞いた患者ID3)log2(After/Before) GSM21763: (退屈な講義を聞いた患者ID5)log2(After/Before) GSM21765: (退屈な講義を聞いた患者ID6)log2(After/Before) GSM21767: (退屈な講義を聞いた患者ID7)log2(After/Before) GSM21769: (退屈な講義を聞いた患者ID10)log2(After/Before) GSM21771: (退屈な講義を聞いた患者ID16)log2(After/Before) GSM21772: (退屈な講義を聞いた患者ID17)log2(After/Before)
のデータです(私の理解が間違ってなければ...)。
param1 <- "GSE1322" #入手したいGEO IDを指定 param2 <- "hoge4_" #出力ファイル名の最初の部分を指定 #必要なパッケージをロード library(GEOquery) #パッケージの読み込み #前処理 eset <- getGEO(param1) #指定したGEO IDのデータを取得した結果をesetに格納 sapply(eset, annotation) #用いられたアレイ情報(GPL ID)を表示 #本番 hoge <- sapply(eset, annotation) #用いられたアレイ情報(GPL ID)をhogeに格納 for(i in 1:length(hoge)){ #hogeの要素数(用いられたアレイ数)分だけループを回す out_f <- paste(param2, hoge[i], ".txt", sep="")#出力ファイル名を作成した結果をout_fに格納 write.exprs(eset[[i]], file=out_f) #outの中身を指定したファイル名で保存。 }
5. AffymetrixデータGSE30533 (Kamei et al., PLoS One, 2013)の発現情報を取得したい場合:
GSE30533は1種類のアレイ(GPL1355)しか使っていないので、1つのファイルのみ生成されます。
param1 <- "GSE30533" #入手したいGEO IDを指定 param2 <- "hoge5_" #出力ファイル名の最初の部分を指定 #必要なパッケージをロード library(GEOquery) #パッケージの読み込み #前処理 eset <- getGEO(param1) #指定したGEO IDのデータを取得した結果をesetに格納 sapply(eset, annotation) #用いられたアレイ情報(GPL ID)を表示 #本番 hoge <- sapply(eset, annotation) #用いられたアレイ情報(GPL ID)をhogeに格納 for(i in 1:length(hoge)){ #hogeの要素数(用いられたアレイ数)分だけループを回す out_f <- paste(param2, hoge[i], ".txt", sep="")#出力ファイル名を作成した結果をout_fに格納 write.exprs(eset[[i]], file=out_f) #outの中身を指定したファイル名で保存。 }
イントロ | アノテーション情報取得 | 公共DB(GEO)から
公共マイクロアレイDBのGene Expression Omnibus (GEO)からアノテーション情報を取得するやり方を紹介します。
-
Gene Expression Omnibus (GEO)のページで「Platforms」をクリック
-
「FIND PLATFORM」をクリック
-
アノテーションを得たいメーカーおよび生物種などを指定してもう一度「FIND PLATFORM」をクリック
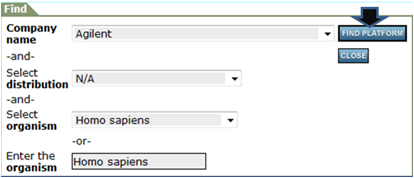
-
いくつかリストアップされる候補の中から目的のチップ(例ではAgilent Human 1A (V2))
につけられているPlatform ID (GPLXXX; 例ではGPL887)をクリック
-
表示されたページの一番したのほうで「Download full table」
(または「Annotation SOFT table」)をクリックして得られるファイル(GPL887-5640.txt)を保存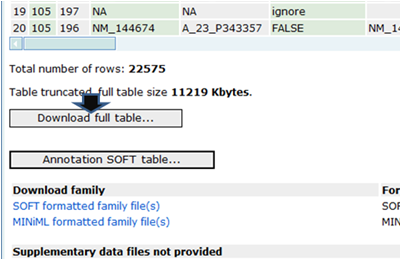
-
機能解析(GSEA周辺)を行いたいときには、以下の作業を行っておいてください。
(i)エクセルでGPL887-5640.txtを開き
(ii)最終的にIDとGene symbolだけからなるGPL887-5640_symbol.txtのようなファイルを作成しておけば、 前処理 | ID変換 | probe ID --> gene symbolや前処理 | ID変換 | 同じ遺伝子名を持つものをまとめるなどの読み込みファイルとして利用可能です。
イントロ | アノテーション情報取得 | GEOquery (Davis_2007)
公共DBGene Expression Omnibus (GEO)に登録されているアレイ(Platform)のアノテーション情報をGEOqueryというRパッケージを用いてゲットするやり方を示します。
「ファイル」−「ディレクトリの変更」でファイルを保存したいディレクトリに移動し以下をコピペ。
1. Affymetrix Rat Genome 230 2.0 Array (GPL1355)のアノテーション情報を知りたい場合:
out_f <- "hoge1.txt" #出力ファイル名を指定してout_fに格納 param <- "GPL1355" #入手したいGEO IDを指定 #必要なパッケージをロード library(GEOquery) #パッケージの読み込み #前処理 data <- getGEO(param) #指定したGEO IDのデータを取得 #本番 out <- data@dataTable@table #アノテーション情報抽出結果をoutに格納 write.table(out, out_f, sep="\t", append=F, quote=F, row.names=F)#outの中身を指定したファイル名で保存
2. "GSE"から始まるIDをたよりにアレイのID情報を内部的に入手してアノテーション情報を取得したい場合:
GSE7623 (Nakai et al., BBB, 2008)は1種類のアレイ(GPL1355)しか使っていないので、1つのファイルのみ生成されます。
param1 <- "GSE7623" #入手したいGEO IDを指定 param2 <- "hoge2_" #出力ファイル名の最初の部分を指定 #必要なパッケージをロード library(GEOquery) #パッケージの読み込み #前処理 data <- getGEO(param1) #指定したGEO IDのデータを取得 sapply(data, annotation) #用いられたアレイ情報(GPL ID)を表示 #本番 hoge <- sapply(data, annotation) #用いられたアレイ情報(GPL ID)をhogeに格納 for(i in 1:length(hoge)){ #hogeの要素数(用いられたアレイ数)分だけループを回す out_f <- paste(param2, hoge[i], ".txt", sep="")#出力ファイル名を作成した結果をout_fに格納 out <- data[[i]]@featureData@data #アノテーション情報抽出結果をoutに格納 write.table(out, out_f, sep="\t", append=F, quote=F, row.names=F)#outの中身を指定したファイル名で保存 }
3. "GSE"から始まるIDをたよりにアレイのID情報を内部的に入手してアノテーション情報を取得したい場合:
GSE7623 (Nakai et al., BBB, 2008)は1種類のアレイ(GPL1355)しか使っていないので、1つのファイルのみ生成されます。 出力ファイルの情報に相当するoutオブジェクト中の、自分がほしいprobe ID列とgene symbol列が1列目と 11列目に存在することがあらかじめ分かっているという前提です。colnames(out)でわかります。 アノテーション情報のバージョンが異なりうるため若干違うかもしれませんがhoge3_GPL1355.txtと酷似したものができていると思います。 Windows10上のRver. 3.3.2にて例題3の動作確認済み(2017/03/08)。
param1 <- "GSE7623" #入手したいGEO IDを指定 param2 <- "hoge3_" #出力ファイル名の最初の部分を指定 param_posi <- c(1, 11) #outオブジェクト中のID列とgene symbol列の位置情報を指定 #必要なパッケージをロード library(GEOquery) #パッケージの読み込み #前処理 data <- getGEO(param1) #指定したGEO IDのデータを取得 sapply(data, annotation) #用いられたアレイ情報(GPL ID)を表示 #本番 hoge <- sapply(data, annotation) #用いられたアレイ情報(GPL ID)をhogeに格納 for(i in 1:length(hoge)){ #hogeの要素数(用いられたアレイ数)分だけループを回す out_f <- paste(param2, hoge[i], ".txt", sep="")#出力ファイル名を作成した結果をout_fに格納 out <- data[[i]]@featureData@data #アノテーション情報抽出結果をoutに格納 colnames(out) #確認してるだけです out <- out[,param_posi] #サブセットを抽出 write.table(out, out_f, sep="\t", append=F, quote=F, row.names=F)#outの中身を指定したファイル名で保存 }
4. "GSE"から始まるIDをたよりにアレイのID情報を内部的に入手してアノテーション情報を取得したい場合:
GSE781は2種類のアレイ(GPL96とGPL97)を使っているので、2つのファイルが生成されます。
param1 <- "GSE781" #入手したいGEO IDを指定 param2 <- "hoge4_" #出力ファイル名の最初の部分を指定 #必要なパッケージをロード library(GEOquery) #パッケージの読み込み #前処理 data <- getGEO(param1) #指定したGEO IDのデータを取得 sapply(data, annotation) #用いられたアレイ情報(GPL ID)を表示 #本番 hoge <- sapply(data, annotation) #用いられたアレイ情報(GPL ID)をhogeに格納 for(i in 1:length(hoge)){ #hogeの要素数(用いられたアレイ数)分だけループを回す out_f <- paste(param2, hoge[i], ".txt", sep="")#出力ファイル名を作成した結果をout_fに格納 out <- data[[i]]@featureData@data #アノテーション情報抽出結果をoutに格納 write.table(out, out_f, sep="\t", append=F, quote=F, row.names=F)#outの中身を指定したファイル名で保存 }
5. Affymetrix Human Transcriptome Array (Gene level: GPL17586)のアノテーション情報を知りたい場合:
out_f <- "hoge5.txt" #出力ファイル名を指定してout_fに格納 param <- "GPL17586" #入手したいGEO IDを指定 #必要なパッケージをロード library(GEOquery) #パッケージの読み込み #前処理 data <- getGEO(param) #指定したGEO IDのデータを取得 #本番 out <- data@dataTable@table #アノテーション情報抽出結果をoutに格納 write.table(out, out_f, sep="\t", append=F, quote=F, row.names=F)#outの中身を指定したファイル名で保存
6. "GSE"から始まるIDをたよりにアレイのID情報を内部的に入手してアノテーション情報を取得したい場合:
GSE1322(Hayashi et al., Psychother Psychosom, 2006)は1種類のアレイ(GPL887)しか使っていないので、1つのファイルのみ生成されます。 出力ファイルの情報に相当するoutオブジェクト中の、自分がほしいprobe ID列とgene symbol列が1列目と 10列目に存在することがあらかじめ分かっているという前提です。colnames(out)でわかります。 アノテーション情報のバージョンが異なりうるため若干違うかもしれませんがhoge6_GPL887.txtと酷似したものができていると思います。
param1 <- "GSE1322" #入手したいGEO IDを指定 param2 <- "hoge6_" #出力ファイル名の最初の部分を指定 param_posi <- c(1, 10) #outオブジェクト中のID列とgene symbol列の位置情報を指定 #必要なパッケージをロード library(GEOquery) #パッケージの読み込み #前処理 data <- getGEO(param1) #指定したGEO IDのデータを取得 sapply(data, annotation) #用いられたアレイ情報(GPL ID)を表示 #本番 hoge <- sapply(data, annotation) #用いられたアレイ情報(GPL ID)をhogeに格納 for(i in 1:length(hoge)){ #hogeの要素数(用いられたアレイ数)分だけループを回す out_f <- paste(param2, hoge[i], ".txt", sep="")#出力ファイル名を作成した結果をout_fに格納 out <- data[[i]]@featureData@data #アノテーション情報抽出結果をoutに格納 colnames(out) #確認してるだけです out <- out[,param_posi] #サブセットを抽出 write.table(out, out_f, sep="\t", append=F, quote=F, row.names=F)#outの中身を指定したファイル名で保存 }
イントロ | アノテーション情報取得 | Rのパッケージ*.dbから
Affymetrix, Agilent, Illumina製など様々な製造メーカーの製品のアノテーション情報を取得するやり方を示します。 数多くの製品(約200 chips)がありますので、詳しくは「全パッケージリスト(All Packages)」中の 「ChipName」をご覧ください。 ただし、Rで提供されていないものも多数ありますのでご注意ください。(例:Agilent-014850 Whole Human Genome Microarray 4x44K G4112F; GPL6480; 2013年8月14日調べ)
「ChipName」のリストを眺めることで、例えばNakai et al., BBB, 2008で用いられた 「Affymetrix Rat Genome 230 2.0 Array」のアノテーション情報はrat2302.dbに含まれていることが分かります。 このようにして、適宜自分が欲しいチップのアノテーション情報がどのような名前で入手できるのか調べた上で、以下のようにします。1. Affymetrix Rat Genome 230 2.0 Array (rat2302.db; GPL1355)の場合:
out_f <- "hoge1.txt" #出力ファイル名を指定してout_fに格納 param1 <- "rat2302.db" #パッケージ名を指定 param2 <- c("REFSEQ", "SYMBOL", "GENENAME")#欲しいアノテーション情報を指定(記述可能なリストは以下のkeytypes(dbname)から取得可能) #必要なパッケージのインストール(利用したいパッケージが既に存在していれば2回目以降は必要なし) source("http://bioconductor.org/biocLite.R")#指定したパッケージのインストール biocLite(param1, suppressUpdates=TRUE) #指定したパッケージのインストール #必要なパッケージをロード library(param1, character.only=T) #指定したパッケージの読み込み #前処理(抽出可能な情報のリストアップおよびキーを表示) hoge <- eval(parse(text=param1)) #オブジェクト名の変更(hogeとして取り扱う) cols(hoge) #hoge中に含まれている情報を表示 keytypes(hoge) #hogeから実際に使用するキーを表示 param_key <- keys(hoge, keytype="PROBEID")#param1で指定したものをキーにしている #本番 out <- select(hoge, keys=param_key, keytype="PROBEID", columns=param2)#アノテーション情報抽出結果をoutに格納 write.table(out, out_f, sep="\t", append=F, quote=F, row.names=F)#outの中身を指定したファイル名で保存
2. Affymetrix Rat Genome 230 2.0 Array (rat2302.db; GPL1355)でプローブIDとgene symbolの対応情報のみ欲しい場合:
out_f <- "hoge2.txt" #出力ファイル名を指定してout_fに格納 param1 <- "rat2302.db" #パッケージ名を指定 param2 <- "SYMBOL" #欲しいアノテーション情報を指定(記述可能なリストは以下のkeytypes(dbname)から取得可能) #必要なパッケージのインストール(利用したいパッケージが既に存在していれば2回目以降は必要なし) source("http://bioconductor.org/biocLite.R")#指定したパッケージのインストール biocLite(param1, suppressUpdates=TRUE) #指定したパッケージのインストール #必要なパッケージをロード library(param1, character.only=T) #param1で指定したパッケージの読み込み #前処理(抽出可能な情報のリストアップおよびキーを表示) hoge <- eval(parse(text=param1)) #オブジェクト名の変更(hogeとして取り扱う) cols(hoge) #hoge中に含まれている情報を表示 keytypes(hoge) #hogeから実際に使用するキーを表示 param_key <- keys(hoge, keytype="PROBEID")#param1で指定したものをキーにしている #本番 out <- select(hoge, keys=param_key, keytype="PROBEID", columns=param2)#アノテーション情報抽出結果をoutに格納 write.table(out, out_f, sep="\t", append=F, quote=F, row.names=F)#outの中身を指定したファイル名で保存
3. Illumina MouseWG-6 v2.0 Expression BeadChip (illuminaMousev2.db; GPL6887)の場合:
out_f <- "hoge3.txt" #出力ファイル名を指定してout_fに格納 param1 <- "illuminaMousev2.db" #パッケージ名を指定 param2 <- c("REFSEQ", "SYMBOL", "GENENAME", "CHRLOC", "ENSEMBLTRANS")#欲しいアノテーション情報を指定(記述可能なリストは以下のkeytypes(dbname)から取得可能) #必要なパッケージのインストール(利用したいパッケージが既に存在していれば2回目以降は必要なし) source("http://bioconductor.org/biocLite.R")#指定したパッケージのインストール biocLite(param1, suppressUpdates=TRUE) #指定したパッケージのインストール #必要なパッケージをロード library(param1, character.only=T) #param1で指定したパッケージの読み込み #前処理(抽出可能な情報のリストアップおよびキーを表示) hoge <- eval(parse(text=param1)) #オブジェクト名の変更(hogeとして取り扱う) cols(hoge) #hoge中に含まれている情報を表示 keytypes(hoge) #hogeから実際に使用するキーを表示 param_key <- keys(hoge, keytype="PROBEID")#param1で指定したものをキーにしている #本番 out <- select(hoge, keys=param_key, keytype="PROBEID", columns=param2)#アノテーション情報抽出結果をoutに格納 write.table(out, out_f, sep="\t", append=F, quote=F, row.names=F)#outの中身を指定したファイル名で保存
4. Agilent Whole Human Genome Oligo Microarray G4112A (hgug4112a.db; GPL1708)の場合:
out_f <- "hoge4.txt" #出力ファイル名を指定してout_fに格納 param1 <- "hgug4112a.db" #パッケージ名を指定 param2 <- c("REFSEQ", "SYMBOL") #欲しいアノテーション情報を指定(記述可能なリストは以下のkeytypes(dbname)から取得可能) #必要なパッケージのインストール(利用したいパッケージが既に存在していれば2回目以降は必要なし) source("http://bioconductor.org/biocLite.R")#指定したパッケージのインストール biocLite(param1, suppressUpdates=TRUE) #指定したパッケージのインストール #必要なパッケージをロード library(param1, character.only=T) #param1で指定したパッケージの読み込み #前処理(抽出可能な情報のリストアップおよびキーを表示) hoge <- eval(parse(text=param1)) #オブジェクト名の変更(hogeとして取り扱う) cols(hoge) #hoge中に含まれている情報を表示 keytypes(hoge) #hogeから実際に使用するキーを表示 param_key <- keys(hoge, keytype="PROBEID")#param1で指定したものをキーにしている #本番 out <- select(hoge, keys=param_key, keytype="PROBEID", columns=param2)#アノテーション情報抽出結果をoutに格納 write.table(out, out_f, sep="\t", append=F, quote=F, row.names=F)#outの中身を指定したファイル名で保存
イントロ | プローブ配列情報取得 | Rのパッケージから
Affymetrix, Agilent, Illumina製など様々な製造メーカーの製品のプローブ配列情報を取得するやり方を示します。 数多くの製品(約200 chips)がありますので、詳しくは「全パッケージリスト(All Packages)」中の 「ChipName」をご覧ください。 ただし、Rで提供されていないものも多数ありますのでご注意ください。(例:Agilent-014850 Whole Human Genome Microarray 4x44K G4112F; GPL6480; 2013年8月14日調べ)
「ChipName」のリストを眺めることで、例えばNakai et al., BBB, 2008で用いられた 「Affymetrix Rat Genome 230 2.0 Array」のプローブ配列情報はrat2302probeに含まれていることが分かります。 このようにして、適宜自分が欲しいチップのプローブ配列情報がどのような名前で入手できるのか調べた上で、以下のようにします。1. Affymetrix Human Genome U133 Plus 2.0 Array (hgu133plus2probe; GPL570)の場合:
out_f <- "hoge1.txt" #出力ファイル名を指定してout_fに格納 param <- "hgu133plus2probe" #パッケージ名を指定 #必要なパッケージをロード library(param, character.only=T) #paramで指定したパッケージの読み込み #前処理(統一的なオブジェクト名に変更しているだけ) hoge <- eval(parse(text=param)) #オブジェクト名の変更(hogeとして取り扱う) #本番(ファイルに保存) write.table(hoge, out_f, sep="\t", append=F, quote=F, row.names=F)#hogeの中身を指定したファイル名で保存
2. Affymetrix Human Genome U133 Plus 2.0 Array (hgu133plus2probe; GPL570)の場合:
(指定したプローブセットIDのみ抽出するやり方です)
out_f <- "hoge2.txt" #出力ファイル名を指定してout_fに格納 param1 <- "hgu133plus2probe" #パッケージ名を指定 param2 <- "1552263_at" #プローブセットID情報を指定 #必要なパッケージをロード library(param1, character.only=T) #param1で指定したパッケージの読み込み #前処理(統一的なオブジェクト名に変更しているだけ) hoge <- eval(parse(text=param1)) #オブジェクト名の変更(hogeとして取り扱う) #本番(フィルタリング) obj <- is.element(as.character(hoge$Probe.Set.Name), param2)#条件を満たすかどうかを判定した結果をobjに格納 out <- hoge[obj,] #objがTRUEとなる行のみ抽出した結果をoutに格納 #ファイルに保存 write.table(out, out_f, sep="\t", append=F, quote=F, row.names=F)#hogeの中身を指定したファイル名で保存
3. Affymetrix Human Genome U133 Plus 2.0 Array (hgu133plus2probe; GPL570)の場合:
(指定したプローブセットIDのみmulti-FASTA形式で保存するやり方です)
out_f <- "hoge3.txt" #出力ファイル名を指定してout_fに格納 param1 <- "hgu133plus2probe" #パッケージ名を指定 param2 <- "1552263_at" #プローブセットID情報を指定 #必要なパッケージをロード library(Biostrings) #パッケージの読み込み library(param1, character.only=T) #param1で指定したパッケージの読み込み #前処理(統一的なオブジェクト名に変更しているだけ) hoge <- eval(parse(text=param1)) #オブジェクト名の変更(hogeとして取り扱う) #本番(フィルタリング) obj <- is.element(as.character(hoge$Probe.Set.Name), param2)#条件を満たすかどうかを判定した結果をobjに格納 out <- hoge[obj,] #objがTRUEとなる行のみ抽出した結果をoutに格納 #後処理(FASTA形式に変換) fasta <- DNAStringSet(out$sequence) #塩基配列情報をDNAStringSetオブジェクトとしてfastaに格納 description <- paste(out$Probe.Set.Name, out$Probe.Interrogation.Position, sep=".")#description部分を作成 names(fasta) <- description #description行に相当する記述を追加している #ファイルに保存 writeXStringSet(fasta, file=out_f, format="fasta", width=50)#fastaの中身を指定したファイル名で保存
4. Affymetrix Rat Genome 230 2.0 Array (rat2302probe; GPL1355)の場合:
(指定したプローブセットIDのみmulti-FASTA形式で保存するやり方です)
out_f <- "hoge4.txt" #出力ファイル名を指定してout_fに格納 param1 <- "rat2302probe" #パッケージ名を指定 param2 <- "1369078_at" #プローブセットID情報を指定 #必要なパッケージをロード library(Biostrings) #パッケージの読み込み library(param1, character.only=T) #param1で指定したパッケージの読み込み #前処理(統一的なオブジェクト名に変更しているだけ) hoge <- eval(parse(text=param1)) #オブジェクト名の変更(hogeとして取り扱う) #本番(フィルタリング) obj <- is.element(as.character(hoge$Probe.Set.Name), param2)#条件を満たすかどうかを判定した結果をobjに格納 out <- hoge[obj,] #objがTRUEとなる行のみ抽出した結果をoutに格納 #後処理(FASTA形式に変換) fasta <- DNAStringSet(out$sequence) #塩基配列情報をDNAStringSetオブジェクトとしてfastaに格納 description <- paste(out$Probe.Set.Name, out$Probe.Interrogation.Position, sep=".")#description部分を作成 names(fasta) <- description #description行に相当する記述を追加している #ファイルに保存 writeXStringSet(fasta, file=out_f, format="fasta", width=50)#fastaの中身を指定したファイル名で保存
イントロ | トランスクリプトーム配列取得 | biomaRt(Durinck_2009)
biomaRtというRパッケージ(Durinck et al., Nat Protoc., 2009)を用いて、 各種アレイ上に搭載されているプローブセットに対応する転写物(トランスクリプトーム)配列を取得するやり方を示します。
「ファイル」−「ディレクトリの変更」でファイルを保存したいディレクトリに移動し以下をコピペ。
1. Affymetrix Rat Genome 230 2.0 Array (GPL1355)に搭載されている転写物のcDNA配列を取得したい場合:
ラット(Rattus norvegicus)アレイだとわかっているので以下のようなオプションを指定しています。
out_f <- "hoge1.txt" #出力ファイル名を指定してout_fに格納 param_dataset <- "rnorvegicus_gene_ensembl"#データセット名を指定(「listDatasets(useMart("ensembl"))」にリストアップされているものを指定可能) param_attribute <- "affy_rat230_2" #配列を取得したい属性名を指定(「listAttributes(mart)」にリストアップされているものを指定可能) param_seqtype <- "cdna" #配列のタイプを指定(cdna, peptide, 3utr, 5utr, genomicのいずれかが指定可能です) #必要なパッケージをロード library(biomaRt) #パッケージの読み込み #前処理(IDリスト情報を取得) mart <- useMart("ensembl",dataset=param_dataset)#データベース名("ensembl")とparam_datasetで指定したデータセット名を与えてmartに格納 hoge <- getBM(attributes=param_attribute, filters="", values="", mart=mart)#指定したIDリスト取得結果をhogeに格納 head(hoge) #確認してるだけです length(hoge) #ID数を表示 #本番(配列取得) out <- getSequence(id=hoge, type=param_attribute, seqType=param_seqtype, mart=mart)#指定したパラメータで配列取得した結果をoutに格納 dim(out) #配列数がID数に比べて若干少ないのは複数のプローブセットが同じ転写物由来なためです。 #ファイルに保存 exportFASTA(out, file=out_f) #outの中身を指定したファイル名で保存
2. Affymetrix Rat Genome 230 2.0 Array (GPL1355)に搭載されている転写物の5' UTR配列を取得したい場合:
上で得られたファイルと比較すると、転写開始点の手前までの配列だけになっていることがわかります。
out_f <- "hoge2.txt" #出力ファイル名を指定してout_fに格納 param_dataset <- "rnorvegicus_gene_ensembl"#データセット名を指定(「listDatasets(useMart("ensembl"))」にリストアップされているものを指定可能) param_attribute <- "affy_rat230_2" #配列を取得したい属性名を指定(「listAttributes(mart)」にリストアップされているものを指定可能) param_seqtype <- "5utr" #配列のタイプを指定(cdna, peptide, 3utr, 5utr, genomicのいずれかが指定可能です) #必要なパッケージをロード library(biomaRt) #パッケージの読み込み #前処理(IDリスト情報を取得) mart <- useMart("ensembl",dataset=param_dataset)#データベース名("ensembl")とparam_datasetで指定したデータセット名を与えてmartに格納 hoge <- getBM(attributes=param_attribute, filters="", values="", mart=mart)#指定したIDリスト取得結果をhogeに格納 head(hoge) #確認してるだけです length(hoge) #ID数を表示 #本番(配列取得) out <- getSequence(id=hoge, type=param_attribute, seqType=param_seqtype, mart=mart)#指定したパラメータで配列取得した結果をoutに格納 dim(out) #配列数を表示 #ファイルに保存 exportFASTA(out, file=out_f) #outの中身を指定したファイル名で保存
3. Affymetrix Rat Genome 230 2.0 Array (GPL1355)に搭載されている特定のプローブセット("1369078_at")のcDNA配列を取得したい場合:
param_valueという追加オプションがあるだけです。
out_f <- "hoge3.txt" #出力ファイル名を指定してout_fに格納 param_dataset <- "rnorvegicus_gene_ensembl"#データセット名を指定(「listDatasets(useMart("ensembl"))」にリストアップされているものを指定可能) param_attribute <- "affy_rat230_2" #配列を取得したい属性名を指定(「listAttributes(mart)」にリストアップされているものを指定可能) param_seqtype <- "cdna" #配列のタイプを指定(cdna, peptide, 3utr, 5utr, genomicのいずれかが指定可能です) param_value <- "1369078_at" #プローブセットIDを指定 #必要なパッケージをロード library(biomaRt) #パッケージの読み込み #前処理 mart <- useMart("ensembl",dataset=param_dataset)#データベース名("ensembl")とparam_datasetで指定したデータセット名を与えてmartに格納 #本番(配列取得) out <- getSequence(id=param_value, type=param_attribute, seqType=param_seqtype, mart=mart)#指定したパラメータで配列取得した結果をoutに格納 dim(out) #配列数がID数に比べて若干少ないのは複数のプローブセットが同じ転写物由来なためです。 #ファイルに保存 exportFASTA(out, file=out_f) #outの中身を指定したファイル名で保存
4. アレイへの搭載の有無にかかわらず、ラットの全転写物のcDNA配列を取得したい場合:
条件を緩くしているのでより多くの配列を取得できていることがわかります。
out_f <- "hoge4.txt" #出力ファイル名を指定してout_fに格納 param_dataset <- "rnorvegicus_gene_ensembl"#データセット名を指定(「listDatasets(useMart("ensembl"))」にリストアップされているものを指定可能) param_attribute <- "ensembl_gene_id" #配列を取得したい属性名を指定(「listAttributes(mart)」にリストアップされているものを指定可能) param_seqtype <- "cdna" #配列のタイプを指定(cdna, peptide, 3utr, 5utr, genomicのいずれかが指定可能です) #必要なパッケージをロード library(biomaRt) #パッケージの読み込み #前処理(IDリスト情報を取得) mart <- useMart("ensembl",dataset=param_dataset)#データベース名("ensembl")とparam_datasetで指定したデータセット名を与えてmartに格納 hoge <- getBM(attributes=param_attribute, filters="", values="", mart=mart)#指定したIDリスト取得結果をhogeに格納 head(hoge) #確認してるだけです length(hoge) #ID数を表示 #本番(配列取得) out <- getSequence(id=hoge, type=param_attribute, seqType=param_seqtype, mart=mart)#指定したパラメータで配列取得した結果をoutに格納 dim(out) #配列数を表示 #ファイルに保存 exportFASTA(out, file=out_f) #outの中身を指定したファイル名で保存
5. Ensembl Gene IDをキーとしてヒトの全転写物のcDNA配列を取得したい場合:
out_f <- "hoge5.txt" #出力ファイル名を指定してout_fに格納 param_dataset <- "hsapiens_gene_ensembl"#データセット名を指定(「listDatasets(useMart("ensembl"))」にリストアップされているものを指定可能) param_attribute <- "ensembl_gene_id" #配列を取得したい属性名を指定(「listAttributes(mart)」にリストアップされているものを指定可能) param_seqtype <- "cdna" #配列のタイプを指定(cdna, peptide, 3utr, 5utr, genomicのいずれかが指定可能です) #必要なパッケージをロード library(biomaRt) #パッケージの読み込み #前処理(IDリスト情報を取得) mart <- useMart("ensembl",dataset=param_dataset)#データベース名("ensembl")とparam_datasetで指定したデータセット名を与えてmartに格納 hoge <- getBM(attributes=param_attribute, filters="", values="", mart=mart)#指定したIDリスト取得結果をhogeに格納 head(hoge) #確認してるだけです length(hoge) #ID数を表示 #本番(配列取得) out <- getSequence(id=hoge, type=param_attribute, seqType=param_seqtype, mart=mart)#指定したパラメータで配列取得した結果をoutに格納 #ファイルに保存 exportFASTA(out, file=out_f) #outの中身を指定したファイル名で保存
6. RefSeq mRNAをキーとしてヒトの全転写物のcDNA配列を取得したい場合:
out_f <- "hoge6.txt" #出力ファイル名を指定してout_fに格納 param_dataset <- "hsapiens_gene_ensembl"#データセット名を指定(「listDatasets(useMart("ensembl"))」にリストアップされているものを指定可能) param_attribute <- "refseq_mrna" #配列を取得したい属性名を指定(「listAttributes(mart)」にリストアップされているものを指定可能) param_seqtype <- "cdna" #配列のタイプを指定(cdna, peptide, 3utr, 5utr, genomicのいずれかが指定可能です) #必要なパッケージをロード library(biomaRt) #パッケージの読み込み #前処理(IDリスト情報を取得) mart <- useMart("ensembl",dataset=param_dataset)#データベース名("ensembl")とparam_datasetで指定したデータセット名を与えてmartに格納 hoge <- getBM(attributes=param_attribute, filters="", values="", mart=mart)#指定したIDリスト取得結果をhogeに格納 head(hoge) #確認してるだけです length(hoge) #ID数を表示 #本番(配列取得) out <- getSequence(id=hoge, type=param_attribute, seqType=param_seqtype, mart=mart)#指定したパラメータで配列取得した結果をoutに格納 #ファイルに保存 exportFASTA(out, file=out_f) #outの中身を指定したファイル名で保存
7. RefSeq mRNAをキーとしてヒトの特定のID("NM_138957")のcDNA配列を取得したい場合:
param_valueという追加オプションがあるだけです。
out_f <- "hoge7.txt" #出力ファイル名を指定してout_fに格納 param_dataset <- "hsapiens_gene_ensembl"#データセット名を指定(「listDatasets(useMart("ensembl"))」にリストアップされているものを指定可能) param_attribute <- "refseq_mrna" #配列を取得したい属性名を指定(「listAttributes(mart)」にリストアップされているものを指定可能) param_seqtype <- "cdna" #配列のタイプを指定(cdna, peptide, 3utr, 5utr, genomicのいずれかが指定可能です) param_value <- "NM_138957" #IDを指定 #必要なパッケージをロード library(biomaRt) #パッケージの読み込み #前処理 mart <- useMart("ensembl",dataset=param_dataset)#データベース名("ensembl")とparam_datasetで指定したデータセット名を与えてmartに格納 #本番(配列取得) out <- getSequence(id=param_value, type=param_attribute, seqType=param_seqtype, mart=mart)#指定したパラメータで配列取得した結果をoutに格納 #ファイルに保存 exportFASTA(out, file=out_f) #outの中身を指定したファイル名で保存
イントロ | トランスクリプトーム配列取得 | annotateパッケージ
annotateというRパッケージを用いて、 任意のGenbank accession番号の塩基配列を取得するやり方を示します。アレイ上に搭載されているプローブセットIDとGenbank accessionの対応関係を関係を得るところも一応できますが、このパッケージ中で用いているgetSEQ関数が複数のGenbank accession番号指定を受け付けないので、ここでは入力が単一のGenbank accession番号、出力がそれに対応した塩基配列情報になります。
「ファイル」−「ディレクトリの変更」でファイルを保存したいディレクトリに移動し以下をコピペ。
1. "NM_031237"の塩基配列を取得したい場合(基本形):
Affymetrix Rat Genome 230 2.0 Array (GPL1355)に搭載されているプローブセット("1367456_at")に対応するGenbank accession IDです。
param <- "NM_031237" #Genbank accession番号を指定 #必要なパッケージをロード library(annotate) #パッケージの読み込み #本番(配列取得) out <- getSEQ(param) #指定したパラメータで配列取得した結果をoutに格納 out #確認してるだけです
2. "NM_031237"の塩基配列を取得してFASTA形式ファイルで保存したい場合:
seqinrパッケージ中のwrite.fasta関数を利用するやり方です。
out_f <- "hoge2.txt" #出力ファイル名を指定してout_fに格納 param <- "NM_031237" #Genbank accession番号を指定 #必要なパッケージをロード library(annotate) #パッケージの読み込み library(seqinr) #パッケージの読み込み #本番(配列取得) out <- getSEQ(param) #指定したパラメータで配列取得した結果をoutに格納 out #確認してるだけです #ファイルに保存 write.fasta(out, names=param, file.out=out_f, nbchar=50)#outの中身を指定したファイル名で保存
イントロ | Affymetrix CELファイル | 各種情報取得
Affymetrix GeneChipのプローブレベルデータは、CELという拡張子がつけられたファイルに収められています。 通常はこのデータにアクセスする必要はありませんが、パーフェクトマッチプローブ(PM)やミスマッチプローブ(MM)のシグナル強度の情報などにアクセスしたい場合には、以下を参考にしてください。
1. AffymetrixデータGSE30533 (Kamei et al., PLoS One, 2013)のCELファイル取得から行う場合:
Affymetrix Rat Genome 230 2.0 Array (GPL1355)を用いて得られたデータです
プローブシグナル強度情報取得や、アレイ上に搭載されているプローブ数情報の取得例です。
param <- "GSE30533" #入手したいIDを指定 #必要なパッケージをロード library(ArrayExpress) #パッケージの読み込み library(affy) #パッケージの読み込み #前処理(データ取得) hoge <- ArrayExpress(param, save=F) #paramで指定したIDのCELファイルなどを取得した結果をhogeに格納 hoge #確認してるだけです sampleNames(hoge) #読み込んだCELファイル名を表示 #本番(各種情報取得) PM <- pm(hoge) #PMプローブシグナル強度情報を取得した結果をPMに格納 head(PM) #確認してるだけです MM <- mm(hoge) #MMプローブシグナル強度情報を取得した結果をMMに格納 head(MM) #確認してるだけです length(PM[,1]) #このアレイ上に搭載されているPMプローブ数を表示 length(MM[,1]) #このアレイ上に搭載されているMMプローブ数を表示
2. AffymetrixデータGSE30533 (Kamei et al., PLoS One, 2013)のCELファイル取得から行う場合:
MMプローブシグナル強度がPMプローブシグナル強度よりも高いものが20%程度以上あるという例示です。
param <- "GSE30533" #入手したいIDを指定 #必要なパッケージをロード library(ArrayExpress) #パッケージの読み込み library(affy) #パッケージの読み込み #前処理(データ取得) hoge <- ArrayExpress(param, save=F) #paramで指定したIDのCELファイルなどを取得した結果をhogeに格納 #本番(PM-MMシグナルの値がマイナスになるものがどれくらいの割合を占めるのか調べる) PM <- pm(hoge) #PMプローブシグナル強度情報を取得した結果をPMに格納 MM <- mm(hoge) #MMプローブシグナル強度情報を取得した結果をMMに格納 out <- PM - MM #PM - MM計算結果をoutに格納 length(out) #行列outの全要素数を表示 sum(out > 0) #(PM - MM) > 0となる要素数を表示 sum(out <= 0) #(PM - MM) <= 0となる要素数を表示 sum(out <= 0) / length(out) #(PM - MM) <= 0となった割合を表示 mean(MM >= PM) #(MM >= PM)となった割合を表示 mean(MM > PM) #(MM > PM)となった割合を表示
3. AffymetrixデータGSE30533 (Kamei et al., PLoS One, 2013)のCELファイル取得から行う場合:
特定のprobesetIDのPMおよびMMシグナル強度情報のみ取得する例です。8番目のプローブでMM > PMとなっていることがわかります。
param1 <- "GSE30533" #入手したいGSE IDを指定 param2 <- "1369078_at" #プローブセットIDを指定 #必要なパッケージをロード library(ArrayExpress) #パッケージの読み込み library(affy) #パッケージの読み込み #前処理(データ取得) hoge <- ArrayExpress(param1, save=F) #paramで指定したIDのCELファイルなどを取得した結果をhogeに格納 sampleNames(hoge) #確認してるだけです(サンプル名およびその順番を) hoge <- hoge[,1] #一つめのサンプルの情報のみ抽出した結果をhogeに格納 sampleNames(hoge) #確認してるだけです #本番(目的のprobeset IDのシグナル強度情報のみ抽出) PM <- pm(hoge, param2) #PMプローブシグナル強度情報を取得した結果をPMに格納 MM <- mm(hoge, param2) #MMプローブシグナル強度情報を取得した結果をMMに格納 PM #確認してるだけです MM #確認してるだけです
4. AffymetrixデータGSE30533 (Kamei et al., PLoS One, 2013)のCELファイル取得から行う場合:
特定のprobesetIDのPMおよびMMシグナル強度情報のみ取得して、折れ線グラフのファイルを作成しています。
out_f <- "hoge4.png" #出力ファイル名を指定してout_fに格納 param1 <- "GSE30533" #入手したいGSE IDを指定 param2 <- "1369078_at" #プローブセットIDを指定 param_fig <- c(500, 300) #ファイル出力時の横幅と縦幅を指定(単位はピクセル) #必要なパッケージをロード library(ArrayExpress) #パッケージの読み込み library(affy) #パッケージの読み込み #前処理(データ取得) hoge <- ArrayExpress(param1, save=F) #paramで指定したIDのCELファイルなどを取得した結果をhogeに格納 hoge <- hoge[,1] #一つめのサンプルの情報のみ抽出した結果をhogeに格納 sampleNames(hoge) #確認してるだけです #本番(目的のprobeset IDのシグナル強度情報のみ抽出) PM <- pm(hoge, param2) #PMプローブシグナル強度情報を取得した結果をPMに格納 MM <- mm(hoge, param2) #MMプローブシグナル強度情報を取得した結果をMMに格納 #ファイルに保存 png(out_f, pointsize=13, width=param_fig[1], height=param_fig[2])#出力ファイルの各種パラメータを指定 min <- min(c(PM, MM)) #y軸の範囲を決めるべく、PMとMMの数値ベクトル中の最小値を取得している max <- max(c(PM, MM)) #y軸の範囲を決めるべく、PMとMMの数値ベクトル中の最大値を取得している ylim <- c(min, max) #y軸の範囲情報をylimに格納 plot(PM, ylim=ylim, ylab="Intensity", #PMシグナル強度をプロット pch=20, type="o", col="black") #PMシグナル強度をプロット par(new=T) #図の重ね書き指定 plot(MM, ylim=ylim, ylab="", #MMシグナル強度をプロット pch=20, type="o", col="gray") #MMシグナル強度をプロット title(param2) #図のタイトルを追加 legend("topright", c("PM", "MM"), #図の凡例を追加 col=c("black", "gray"), pch=20) #図の凡例を追加 dev.off() #おまじない
正規化(cDNA or two-color or 二色法) について
私はこのあたりについては明るくありませんが、Loess, Splines, Waveletsがよく用いられているようです。このほかにKernel smootingとSupport Vector Regression (SVR)を含めた計5つの正規化法を比較した論文(Fujita et al., BMC Bioinformatics, 2006)によると、SVRが最もよいそうです。
Agilent two-colorアレイについては、MAQCのExternal RNA Controls (ERCs)のデータを評価に用いた場合、「Agilent's Feature Extraction software(という専用のdata processing法があるらしい)」よりも単純に「loess正規化」をかけたもののほうがうまく既知のERCsをlog ratioの軸で分離できるという報告(Kerr KF., BMC Bioinformatics, 2007)があります。
正規化 | dual channel (Stanford型マイクロアレイ) (package:limma)
Linear Models for Microarray Data (limma)。ArrayVision, ImaGene, GenePix, QuantArray, or SPOTのアウトプットファイルを入力とすることができるらしい。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動。
library(limma) #パッケージの読み込み limmaUsersGuide() #詳しい説明(PDFファイルが開く)
正規化 - dual channel (Stanford型マイクロアレイ) (package:marray)
GenePix fileをそのまま読み込むことができるらしい。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動。
#必要なパッケージをロード library(marray) #パッケージの読み込み
正規化 | Agilent microarray | について
このあたりはよくわかっていません。正規化という項目にとりあえず入れていますが、データの読み込みから解析まで一通りできるものと思われます。 limmaパッケージは「Reading Single-Channel Agilent Intensity Data」という項目があったので、おそらく一連の解析ができるものと思われます。 BABARパッケージはGenePix or BlueFuse microarray data filesのみ受けつけと書いていたので適用外かもしれません。
R用:
Review、ガイドライン、パイプライン系:
正規化 | Agilent microarray | agilp (Chain_2010)
agilpパッケージを用いたやり方を示します。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動。
#必要なパッケージをロード library(agilp) #パッケージの読み込み
正規化 | Illumina BeadArray | について
このあたりはよくわかっていません。正規化という項目にとりあえず入れていますが、データの読み込みから解析まで一通りできるものと思われます。 limmaパッケージは「Reading Illumina BeadChip Data」という項目があったので、おそらく一連の解析ができるものと思われます。
R用:
正規化 | Illumina BeadArray | BeadDataPackR (Smith_2010)
BeadDataPackRパッケージを用いたやり方を示します。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動。
#必要なパッケージをロード library(BeadDataPackR) #パッケージの読み込み
正規化 | Illumina BeadArray | lumi (Du_2008)
lumiパッケージを用いたやり方を示します。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動。
#必要なパッケージをロード library(lumi) #パッケージの読み込み
正規化 | Illumina BeadArray | beadarray (Dunning_2007)
beadarrayパッケージを用いたやり方を示します。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動。
#必要なパッケージをロード library(beadarray) #パッケージの読み込み
正規化 | Affymetrix GeneChip | について
2015年11月に調査した結果をリストアップします。
- MBEI:Li and Wong, PNAS, 2001
- VSN:Huber et al., Bioinformatics, 2002
- MAS5.0:Hubbell et al., Bioinformatics, 2002
- RMA:Irizarry et al., Biostatistics, 2003
- GCRMA:Wu et al., J. Am. Stat. Assoc., 2004
- multi-mgMOS:Liu et al., Bioinformatics, 2005
- FARMS:Hochreiter et al., Bioinformatics, 2006
- Extrapolation Averaging (EA):Goldstein, DR, Bioinformatics, 2006
- FGX(リンク切れ):Purutçuoglu and Wit, Biostatistics, 2007
- refRMA:Katz et al., BMC Bioinformatics, 2006
- DFW:Chen et al., Bioinformatics, 2007
- libaffy:Eschrich et al., Bioinformatics, 2007
- RefPlus(RMA++ and RMA+):Harbron et al., Bioinformatics, 2007
- bgx:Turro et al., BMC Bioinformatics, 2007
- LVS:Calza et al., BMC Bioinformatics, 2008
- Hook:Binder et al., Algorithms Mol. Biol., 2008
- GRSN:Pelz et al., BMC Bioinformatics, 2008
- MMBGX:Turro et al., Nucleic Acids Res., 2010
- fRMA:McCall et al., Biostatistics, 2010
- tRMA:Giorgi et al, BMC Bioinformatics, 2010
- rmx:Kohl and Deigner, BMC Bioinformatics, 2010
- KDL and KDQ (SAS code):Hsieh et al., BMC Bioinformatics, 2011
- RPA:Lahti et al., Nucleic Acids Res., 2013
- IRON in libaffy:Welsh et al., BMC Bioinformatics, 2013
正規化 | Affymetrix GeneChip | frma (McCall_2010)
Affymetrix chip (GeneChip)を用いて得られた*.CELファイルを元に、frozen robust multiarray analysis (fRMA; McCall et al., Biostatistics, 2010)アルゴリズムを用いてSummary scoreを算出。
この方法を利用可能なアレイは限られていますので注意してください。利用可能なアレイリストはこちら。 例えば、そこそこ利用されているAffymetrix Rat Genome 230 2.0 Array(GPL1355)は2013年8月21日現在利用できません。 利用するためには、fRMATools (McCall et al., BMC Bioinformatics, 2011)を利用して、 そのアレイを用いた実験データを沢山集めてパラメータ推定(frozen parameter estimates)を行ったデータを作成しておく必要があります。
「ファイル」−「ディレクトリの変更」で適切なディレクトリに移動し以下をコピペ。
1. (CELファイルがあるディレクトリ上で)手元にあるCELファイルの読み込みから行う場合:
summarization法を"robust_weighted_average"にする場合です(default)
out_f <- "hoge1.txt" #出力ファイル名を指定してout_fに格納 param <- "robust_weighted_average" #summarization法を指定 #必要なパッケージをロード library(frma) #パッケージの読み込み library(affy) #パッケージの読み込み #データファイルの読み込み(*.CELファイル) hoge <- ReadAffy() #*.CELファイルの読み込み #本番 eset <- frma(hoge, summarize=param) #fRMAを実行し、結果をesetに保存 #ファイルに保存 write.exprs(eset, file=out_f) #結果を指定したファイル名で保存
2. (CELファイルがあるディレクトリ上で)手元にあるCELファイルの読み込みから行う場合:
summarization法を"median_polish"にする場合です
out_f <- "hoge2.txt" #出力ファイル名を指定してout_fに格納 param <- "median_polish" #summarization法を指定 #必要なパッケージをロード library(frma) #パッケージの読み込み library(affy) #パッケージの読み込み #データファイルの読み込み(*.CELファイル) hoge <- ReadAffy() #*.CELファイルの読み込み #本番 eset <- frma(hoge, summarize=param) #fRMAを実行し、結果をesetに保存 #ファイルに保存 write.exprs(eset, file=out_f) #結果を指定したファイル名で保存
3. AffymetrixデータGSE30533 (Kamei et al., PLoS One, 2013)のCELファイル取得から行う場合:
指定したGSE IDが複数種類のアレイで行われたCELファイルを含んでいたらうまくいかないかもしれません。
out_f <- "hoge3.txt" #出力ファイル名を指定してout_fに格納 param <- "GSE30533" #入手したいIDを指定 #必要なパッケージをロード library(ArrayExpress) #パッケージの読み込み library(frma) #パッケージの読み込み #前処理(データ取得) hoge <- ArrayExpress(param, save=F) #paramで指定したIDのCELファイルなどを取得した結果をhogeに格納 #本番 eset <- frma(hoge, summarize=param) #fRMAを実行し、結果をesetに保存 #ファイルに保存 write.exprs(eset, file=out_f) #結果を指定したファイル名で保存
正規化 | Affymetrix GeneChip | rmx (Kohl_2010)
RobLoxBioCというRパッケージ中に実装されているrobust radius-minimax (rmx) estimatorというsummarization法です。 論文中にMAS5の拡張版と書いてあるように、最後のステップのsummarization score計算時に(MAS5で採用されている)Tukey's biweightの代わりにrmx estimatorを利用しているところがポイントのようです。 サンプルごとに独立して正規化を行っています。 オリジナルはMASと同じくlog変換前のデータになっているので、robloxbioc関数をかけたあとに、自分で1以下の数値を1にした後にlog2変換したものを出力しています。
「ファイル」−「ディレクトリの変更」で適切なディレクトリに移動し以下をコピペ。
1. (CELファイルがあるディレクトリ上で)手元にあるCELファイルの読み込みから行う場合:
out_f <- "hoge1.txt" #出力ファイル名を指定してout_fに格納 #必要なパッケージをロード library(RobLoxBioC) #パッケージの読み込み #データファイルの読み込み(*.CELファイル) hoge <- ReadAffy() #*.CELファイルの読み込み #本番 eset <- robloxbioc(hoge) #rmxを実行し、結果をesetに保存 #対数変換 summary(exprs(eset)) #得られたesetの遺伝子発現行列のシグナル強度分布を表示 exprs(eset)[exprs(eset) < 1] <- 1 #対数変換(log2)できるようにシグナル強度が1未満のものを1にしておく summary(exprs(eset)) #上記処理後のシグナル強度分布を再び表示させて確認 exprs(eset) <- log(exprs(eset), 2) #底を2として対数変換 #ファイルに保存 write.exprs(eset, file=out_f) #結果を指定したファイル名で保存
2. AffymetrixデータGSE30533 (Kamei et al., PLoS One, 2013)のCELファイル取得から行う場合:
指定したGSE IDが複数種類のアレイで行われたCELファイルを含んでいたらうまくいかないかもしれません。
out_f <- "hoge2.txt" #出力ファイル名を指定してout_fに格納 param <- "GSE30533" #入手したいIDを指定 #必要なパッケージをロード library(ArrayExpress) #パッケージの読み込み library(RobLoxBioC) #パッケージの読み込み #前処理(データ取得) hoge <- ArrayExpress(param, save=F) #paramで指定したIDのCELファイルなどを取得した結果をhogeに格納 #本番 eset <- robloxbioc(hoge) #rmxを実行し、結果をesetに保存 #対数変換 summary(exprs(eset)) #得られたesetの遺伝子発現行列のシグナル強度分布を表示 exprs(eset)[exprs(eset) < 1] <- 1 #対数変換(log2)できるようにシグナル強度が1未満のものを1にしておく summary(exprs(eset)) #上記処理後のシグナル強度分布を再び表示させて確認 exprs(eset) <- log(exprs(eset), 2) #底を2として対数変換 #ファイルに保存 write.exprs(eset, file=out_f) #結果を指定したファイル名で保存
3. AffymetrixデータGSE30533 (Kamei et al., PLoS One, 2013)のCELファイル取得から行う場合:
計10サンプルのうち、「最初の2サンプルのみで正規化した結果」と「最初の3サンプルのみ正規化した結果」を表示させています。rmxがper-array basisの正規化法であることがわかります。
param <- "GSE30533" #入手したいIDを指定 #必要なパッケージをロード library(ArrayExpress) #パッケージの読み込み library(RobLoxBioC) #パッケージの読み込み #前処理(データ取得) hoge <- ArrayExpress(param, save=F) #paramで指定したIDのCELファイルなどを取得した結果をhogeに格納 hoge #確認してるだけです sampleNames(hoge) #読み込んだCELファイル名を表示 #本番(最初の2サンプルの正規化) posi <- 1:2 eset <- robloxbioc(hoge[posi]) #rmxを実行し、結果をesetに保存 head(exprs(eset)) #確認してるだけです #本番(最初の3サンプルの正規化) posi <- 1:3 eset <- robloxbioc(hoge[posi]) #rmxを実行し、結果をesetに保存 head(exprs(eset)) #確認してるだけです
正規化 | Affymetrix GeneChip | GRSN (Pelz_2008)
Rコードがsupplementから得られます。項目のみ。
正規化 | Affymetrix GeneChip | Hook (Binder_2008)
Hookの著者らが出したprobe中のGuanine (G)のバイアスに関する2010年の論文(Fasold et al., BMC Bioinformatics, 2010)があります。 Gが三つ以上連続して存在するとシグナル強度が異常に高くなるという傾向があるようで、 これをうまく補正してくれるらしいのがHookというC++/Rプログラムらしいです。私は使ったことがありません。。
- Hookの理論に関する論文:Binder and Preibisch, Algorithms Mol. Biol., 2008
- Hookのchipの特徴に関する論文:Binder et al., Algorithms Mol. Biol., 2008
- Fasold et al., BMC Bioinformatics, 2010
- HookのR-code
正規化 | Affymetrix GeneChip | DFW (Chen_2007)
Affymetrix chip (GeneChipTM)を用いて得られた*.CELファイルを元に、Distribution Free Weighted method(DFW; Chen et al., Bioinformatics, 2007)を用いてSummary scoreを算出。
Affycomp II spike-in datasetによる評価でFARMSなどを含む他の手法よりも感度・特異度の点でよかったとのこと。
しかしこの正規化法は、R ver. 2.7.2あたりだと正常に動作していて、R Ver. 2.8.1以降ではうまく動かない状況が続いていました。2021年6月ごろにR ver. 4.0.5で動かすやり方を教えていただいたので記しておきます(中井雄治 氏提供情報)。情報はとっくにいただいていたのですが、多忙のため反映が2022年4月になってしまい失礼しましたm(_ _)m
1. 「ファイル」−「ディレクトリの変更」で解析したいファイル(*.CELファイル)を置いてあるディレクトリに移動し、以下をコピペ
out_f <- "data_dfw.txt" #出力ファイル名を指定してout_fに格納 #必要な関数などをロード source("http://www.iu.a.u-tokyo.ac.jp/kadota/R/dfw.R")#DFWを実行する関数を含むファイルをあらかじめ読み込む library(affy) #パッケージの読み込み upDate.express.summary.stat.methods(c(express.summary.stat.methods(), "dfw"))#dfw関数を実行できるようにしている #データファイルの読み込み(*.CELファイル) hoge <- ReadAffy() #CELファイルの読み込み #本番 eset <- expresso(hoge, bgcorrect.method="none", normalize.method="quantiles", pmcorrect.method="pmonly", summary.method="dfw")#DFW法を実行し、結果をesetに保存。 #ファイルに保存 write.exprs(eset, file=out_f) #結果を指定したファイル名で保存
- R code for DFW (PDF):Chen et al., Bioinformatics, 2007
- DFWについてのppt資料(p10のexpression valueは明記されていませんがc=0.05のときの値のようですね(defaultは0.01)。
- affy:Gautier et al., Bioinformatics, 2004
正規化 | Affymetrix GeneChip | FARMS (Hochreiter_2006)
Affymetrix chip (GeneChipTM)を用いて得られた*.CELファイルを元に、FARMS (Hochreiter et al., Bioinformatics, 2006)アルゴリズムを用いてSummary scoreを算出。
False positiveもRMA (Irizarry et al., Biostatistics, 2003)やMAS5.0 (Hubbell et al., Bioinformatics, 2002)に比べて少なく、計算時間もRMAより早いとのこと。This package is only free for non-commercial users.だそうです。
FARMSは実際には以下の二つのやり方のいずれかを用いて行います:
- qFarms(no background correction and quantile normalization;計算時間が早いというメリットがあるのでこっちがデフォルト)
- lFarms(no background correction and loess normalization)
2012/05/16現在の最新版は、version1.4.1ですが、実際にダウンロードされる場合は、参考URLで最新版を確認されることをお勧めします。
また、R2.14.2やR2.15.0ではパッケージのインストールがうまくいかなくなっているようです...orz。R2.11.Xあたりだとうまく動くかもしれません。。。 2019/12/28にq.farmsだった関数名をqFarmsに変更しました。(中井雄治 氏提供情報)
パッケージのインストール方法(最初の一回のみ)
- 「ファイル」−「ディレクトリの変更」でデスクトップに移動
- farms_1.4.1.zipファイルをデスクトップにダウンロード
- Rコマンドライン上で以下をコピー&ペースト
install.packages("farms_1.4.1.zip", repos=NULL)
「ファイル」−「ディレクトリの変更」で解析したいファイル(*.CELファイル)を置いてあるディレクトリに移動。
1. qFarms(quantile normalization; デフォルト)の場合:
out_f <- "hoge1.txt" #出力ファイル名を指定してout_fに格納 #必要なパッケージをロード library(affy) #パッケージの読み込み library(farms) #パッケージの読み込み #データファイルの読み込み(*.CELファイル) hoge <- ReadAffy() #*.CELファイルの読み込み #本番 eset <- qFarms(hoge) #qFARMSを実行し、結果をesetに保存 #ファイルに保存 write.exprs(eset, file=out_f) #結果を指定したファイル名で保存
2. lFarms(loess normalization)の場合:
out_f <- "hoge2.txt" #出力ファイル名を指定してout_fに格納 #必要なパッケージをロード library(affy) #パッケージの読み込み library(farms) #パッケージの読み込み #データファイルの読み込み(*.CELファイル) hoge <- ReadAffy() #*.CELファイルの読み込み #本番 eset <- lFarms(hoge) #lFARMSを実行し、結果をesetに保存 #ファイルに保存 write.exprs(eset, file=out_f) #結果を指定したファイル名で保存
正規化 | Affymetrix GeneChip | multi-mgMOS (Liu_2005)
Affymetrix chip (GeneChipTM)を用いて得られた*.CELファイルを元に、pumaパッケージに実装されているmulti-mgMOS法(Liu et al., 2005)を用いてSummary scoreを算出。
(このデータセットは使えないといった)批判的なコメントが多数寄せられている、「いわゆるGolden spike data (Choe et al., 2005)」だけをもとに、 これまた(評判の悪い)「等量でspiked-inされたprobesetsだけ」をもとにしてsummarization後 (MAS, RMA, or multi-mgMOSなどで正規化後、という意味)のデータをさらにloess正規化したものに対してt-testやSAM, Cyber-TなどでAUCを計算してみたら、multi-mgMOSが良かったという論文(Pearson R., BMC Bioinformatics, 2008)があったので、念のため掲載しました。
しかしまあ、Pearson R., BMC Bioinformatics, 2008で評価に用いたのはGolden spike dataだけなのでmulti-mgMOSが本当に使える方法なのかは”かなり”疑問の余地があります。しかも約23,000 probesetsを搭載しているU133Aチップのたった6 arrays程度の正規化でさえ、ものすごく時間がかかります。これだけ遅いと、現実のデータには使えない、ですね。
また、この方法の売りは、MASのPresent/Absent callやFARMSのInformative/non-informative callと同様、計算したシグナル強度(expression level)に対して、そのexpected uncertaintyも計算するところだそうです。 この情報を使ったデータ解析法として、「主成分分析(PCA)の改良版 (Sanguinetti et al., Bioinformatics, 2005)」、「発現変動遺伝子検出法Probability of Positive Log Ratio (PPLR: Liu et al., Bioinformatics, 2006)」などがあり、いずれもpumaライブラリ中にあります。 マニュアルにも、これまた「すごく時間がかかる」といった記述がありましたのであしからず。
「ファイル」−「ディレクトリの変更」で適切なディレクトリに移動し以下をコピペ。
1. (CELファイルがあるディレクトリ上で)手元にあるCELファイルの読み込みから行う場合:
out_f <- "hoge1.txt" #出力ファイル名を指定してout_fに格納 #必要なパッケージをロード library(puma) #パッケージの読み込み #データファイルの読み込み(*.CELファイル) hoge <- ReadAffy() #*.CELファイルの読み込み #本番 eset <- mmgmos(hoge) #multi-mgMOSを実行し、結果をesetに保存 #ファイルに保存 write.exprs(eset, file=out_f) #結果を指定したファイル名で保存
2. AffymetrixデータGSE30533 (Kamei et al., PLoS One, 2013)のCELファイル取得から行う場合:
指定したGSE IDが複数種類のアレイで行われたCELファイルを含んでいたらうまくいかないかもしれません。
out_f <- "hoge2.txt" #出力ファイル名を指定してout_fに格納 param <- "GSE30533" #入手したいIDを指定 #必要なパッケージをロード library(ArrayExpress) #パッケージの読み込み library(puma) #パッケージの読み込み #前処理(データ取得) hoge <- ArrayExpress(param, save=F) #paramで指定したIDのCELファイルなどを取得した結果をhogeに格納 #本番 eset <- mmgmos(hoge) #multi-mgMOSを実行し、結果をesetに保存 #ファイルに保存 write.exprs(eset, file=out_f) #結果を指定したファイル名で保存
- multi-mgMOS:Liu et al., Bioinformatics, 2005
- puma 3.0:Liu et al., BMC Bioinformatics, 2013
- Pearson R., BMC Bioinformatics, 2008
- Choe et al., Genome Biol., 2005
- Sanguinetti et al., Bioinformatics, 2005
- PPLR:Liu et al., Bioinformatics, 2006
- affy:Gautier et al., Bioinformatics, 2004
- ArrayExpress:Kauffmann et al., Bioinformatics, 2009
正規化 | Affymetrix GeneChip | GCRMA (Wu_2004)
Affymetrix chip (GeneChipTM)を用いて得られた*.CELファイルを元に、GCRMA(Wu et al., J. Am. Stat. Assoc., 2004)アルゴリズムを用いてSummary scoreを算出。
「ファイル」−「ディレクトリの変更」で適切なディレクトリに移動し以下をコピペ。
1. (CELファイルがあるディレクトリ上で)手元にあるCELファイルの読み込みから行う場合:
out_f <- "hoge1.txt" #出力ファイル名を指定してout_fに格納 #必要なパッケージをロード library(gcrma) #パッケージの読み込み #データファイルの読み込み(*.CELファイル) hoge <- ReadAffy() #*.CELファイルの読み込み #本番 eset <- gcrma(hoge) #GCRMAを実行し、結果をesetに保存 #ファイルに保存 write.exprs(eset, file=out_f) #結果を指定したファイル名で保存
2. AffymetrixデータGSE30533 (Kamei et al., PLoS One, 2013)のCELファイル取得から行う場合:
指定したGSE IDが複数種類のアレイで行われたCELファイルを含んでいたらうまくいかないかもしれません。
out_f <- "hoge2.txt" #出力ファイル名を指定してout_fに格納 param <- "GSE30533" #入手したいIDを指定 #必要なパッケージをロード library(ArrayExpress) #パッケージの読み込み library(gcrma) #パッケージの読み込み #前処理(データ取得) hoge <- ArrayExpress(param, save=F) #paramで指定したIDのCELファイルなどを取得した結果をhogeに格納 #本番 eset <- gcrma(hoge) #GCRMAを実行し、結果をesetに保存 #ファイルに保存 write.exprs(eset, file=out_f) #結果を指定したファイル名で保存
正規化 | Affymetrix GeneChip | PLIER (Affymetrix_2004)
Affymetrix chip (GeneChipTM)を用いて得られた*.CELファイルを元に、PLIER(Probe Logarithmic Intensity ERror; Affymetrix社(2004-))アルゴリズムを用いてSummary scoreを算出。Affymetrix社提供のMAS5(2002-)アルゴリズムの次のバージョン、だと思っていたがどうやらそういうわけではないらしい(2008/8/20追加)。
論文中で「PLIER+16」という記述をMAQCの論文などでみたことがあるかと思いますが、これは文字通り通常の出力に16を足しただけです。このプログラムについてのR上での説明は非常に不親切で真実は定かではありませんが、値の分布的におそらく以下の結果は「PLIER+16」なんだろうと思います。
また、MAQCの論文(Shi et al., Nat. Biotechnol., 2006)中では「quantile normalizationしてからPLIER」にかけてますので、このやり方も示します。
「ファイル」−「ディレクトリの変更」で適切なディレクトリに移動し以下をコピペ。
1. (CELファイルがあるディレクトリ上で)手元にあるCELファイルの読み込みから行う場合:
「デフォルトのPLIER」です
out_f <- "hoge1.txt" #出力ファイル名を指定してout_fに格納 #必要なパッケージをロード library(plier) #パッケージの読み込み #データファイルの読み込み(*.CELファイル) hoge <- ReadAffy() #*.CELファイルの読み込み #本番 eset <- justPlier(hoge) #PLIERを実行し、結果をesetに保存 #ファイルに保存 write.exprs(eset, file=out_f) #結果を指定したファイル名で保存
2. (CELファイルがあるディレクトリ上で)手元にあるCELファイルの読み込みから行う場合:
「quantile normalizationしてからPLIER」です
out_f <- "hoge2.txt" #出力ファイル名を指定してout_fに格納 #必要なパッケージをロード library(plier) #パッケージの読み込み #データファイルの読み込み(*.CELファイル) hoge <- ReadAffy() #*.CELファイルの読み込み #本番 eset <- justPlier(hoge, normalize=TRUE)#quantile normalizationつきのPLIERを実行し、結果をesetに保存 #ファイルに保存 write.exprs(eset, file=out_f) #結果を指定したファイル名で保存
3. AffymetrixデータGSE30533 (Kamei et al., PLoS One, 2013)のCELファイル取得から行う場合:
「デフォルトのPLIER」です。指定したGSE IDが複数種類のアレイで行われたCELファイルを含んでいたらうまくいかないかもしれません。
out_f <- "hoge3.txt" #出力ファイル名を指定してout_fに格納 param <- "GSE30533" #入手したいIDを指定 #必要なパッケージをロード library(ArrayExpress) #パッケージの読み込み library(plier) #パッケージの読み込み #前処理(データ取得) hoge <- ArrayExpress(param, save=F) #paramで指定したIDのCELファイルなどを取得した結果をhogeに格納 #本番 eset <- justPlier(hoge) #PLIERを実行し、結果をesetに保存 #ファイルに保存 write.exprs(eset, file=out_f) #結果を指定したファイル名で保存
正規化 | Affymetrix GeneChip | VSN (Huber_2002)
Affymetrix chip (GeneChipTM)を用いて得られた*.CELファイルを元に、VSN(Variance stabilization; Huber et al., Bioinformatics, 2002)アルゴリズムを用いてSummary scoreを算出。
VSNはRMAに比べてより低発現領域におけるバラツキのコントロールを厳しくしています。それゆえ、RMAに比べ、より得られるシグナル強度のダイナミックレンジが狭くなります。
「ファイル」−「ディレクトリの変更」で適切なディレクトリに移動し以下をコピペ。
1. (CELファイルがあるディレクトリ上で)手元にあるCELファイルの読み込みから行う場合:
out_f <- "hoge1.txt" #出力ファイル名を指定してout_fに格納 #必要なパッケージをロード library(vsn) #パッケージの読み込み library(affy) #パッケージの読み込み #データファイルの読み込み(*.CELファイル) hoge <- ReadAffy() #*.CELファイルの読み込み #本番 eset <- vsnrma(hoge) #VSNを実行し、結果をesetに保存 #ファイルに保存 write.exprs(eset, file=out_f) #結果を指定したファイル名で保存
2. AffymetrixデータGSE30533 (Kamei et al., PLoS One, 2013)のCELファイル取得から行う場合:
指定したGSE IDが複数種類のアレイで行われたCELファイルを含んでいたらうまくいかないかもしれません。
out_f <- "hoge2.txt" #出力ファイル名を指定してout_fに格納 param <- "GSE30533" #入手したいIDを指定 #必要なパッケージをロード library(ArrayExpress) #パッケージの読み込み library(vsn) #パッケージの読み込み #前処理(データ取得) hoge <- ArrayExpress(param, save=F) #paramで指定したIDのCELファイルなどを取得した結果をhogeに格納 #本番 eset <- vsnrma(hoge) #VSNを実行し、結果をesetに保存 #ファイルに保存 write.exprs(eset, file=out_f) #結果を指定したファイル名で保存
正規化 | Affymetrix GeneChip | RMA (Irizarry_2003)
Affymetrix chip (GeneChipTM)を用いて得られた*.CELファイルを元に、RMA(Irizarry et al., Biostatistics, 2003)アルゴリズムを用いてSummary scoreを算出。
「ファイル」−「ディレクトリの変更」で適切なディレクトリに移動し以下をコピペ。
1. (CELファイルがあるディレクトリ上で)手元にあるCELファイルの読み込みから行う場合:
out_f <- "hoge1.txt" #出力ファイル名を指定してout_fに格納 #必要なパッケージをロード library(affy) #パッケージの読み込み #データファイルの読み込み(*.CELファイル) hoge <- ReadAffy() #*.CELファイルの読み込み #本番 eset <- rma(hoge) #RMAを実行し、結果をesetに保存 #ファイルに保存 write.exprs(eset, file=out_f) #結果を指定したファイル名で保存
2. AffymetrixデータGSE30533 (Kamei et al., PLoS One, 2013)のCELファイル取得から行う場合:
指定したGSE IDが複数種類のアレイで行われたCELファイルを含んでいたらうまくいかないかもしれません。
out_f <- "hoge2.txt" #出力ファイル名を指定してout_fに格納 param <- "GSE30533" #入手したいIDを指定 #必要なパッケージをロード library(ArrayExpress) #パッケージの読み込み library(affy) #パッケージの読み込み #前処理(データ取得) hoge <- ArrayExpress(param, save=F) #paramで指定したIDのCELファイルなどを取得した結果をhogeに格納 #本番 eset <- rma(hoge) #RMAを実行し、結果をesetに保存 #ファイルに保存 write.exprs(eset, file=out_f) #結果を指定したファイル名で保存
正規化 | Affymetrix GeneChip | MAS5.0 (Hubbell_2002)
Affymetrix chip (GeneChipTM)を用いて得られた*.CELファイルを元に、MAS5.0 (Hubbell et al., Bioinformatics, 2002)アルゴリズムを用いてSummary scoreを算出するやり方を示します。 低発現領域でのばらつきが大きいことが指摘されていますが、detection callがAbsentのものを使わないなど適切な利用をすれば決して悪い方法ではない(Pepper et al., BMC Bioinformatics, 2007)という報告もあります。 また、アレイごとに独立して正規化を行うため(per-array basis)、解析するアレイの追加などに影響されないなどの利点があります。
「ファイル」−「ディレクトリの変更」で適切なディレクトリに移動し以下をコピペ。
1. (CELファイルがあるディレクトリ上で)手元にあるCELファイルの読み込みから行う場合:
out_f <- "hoge1.txt" #出力ファイル名を指定してout_fに格納 #必要なパッケージをロード library(affy) #パッケージの読み込み #データファイルの読み込み(*.CELファイル) hoge <- ReadAffy() #*.CELファイルの読み込み #本番 eset <- mas5(hoge) #MASを実行し、結果をesetに保存 #対数変換 summary(exprs(eset)) #得られたesetの遺伝子発現行列のシグナル強度分布を表示 exprs(eset)[exprs(eset) < 1] <- 1 #対数変換(log2)できるようにシグナル強度が1未満のものを1にしておく summary(exprs(eset)) #上記処理後のシグナル強度分布を再び表示させて確認 exprs(eset) <- log(exprs(eset), 2) #底を2として対数変換 #ファイルに保存 write.exprs(eset, file=out_f) #結果を指定したファイル名で保存
2. AffymetrixデータGSE30533 (Kamei et al., PLoS One, 2013)のCELファイル取得から行う場合:
指定したGSE IDが複数種類のアレイで行われたCELファイルを含んでいたらうまくいかないかもしれません。
out_f <- "hoge2.txt" #出力ファイル名を指定してout_fに格納 param <- "GSE30533" #入手したいIDを指定 #必要なパッケージをロード library(ArrayExpress) #パッケージの読み込み library(affy) #パッケージの読み込み #前処理(データ取得) hoge <- ArrayExpress(param, save=F) #paramで指定したIDのCELファイルなどを取得した結果をhogeに格納 #本番 eset <- mas5(hoge) #MASを実行し、結果をesetに保存 #対数変換 summary(exprs(eset)) #得られたesetの遺伝子発現行列のシグナル強度分布を表示 exprs(eset)[exprs(eset) < 1] <- 1 #対数変換(log2)できるようにシグナル強度が1未満のものを1にしておく summary(exprs(eset)) #上記処理後のシグナル強度分布を再び表示させて確認 exprs(eset) <- log(exprs(eset), 2) #底を2として対数変換 #ファイルに保存 write.exprs(eset, file=out_f) #結果を指定したファイル名で保存
3. AffymetrixデータGSE30533 (Kamei et al., PLoS One, 2013)のCELファイル取得から行う場合:
指定したGSE IDが複数種類のアレイで行われたCELファイルを含んでいたらうまくいかないかもしれません。
シグナル強度が1以下のものを1にするという操作を行わずにlog2変換のみ行うやり方です。したがって、logをとれない0の要素が存在するとエラーになります。
out_f <- "hoge3.txt" #出力ファイル名を指定してout_fに格納 param <- "GSE30533" #入手したいIDを指定 #必要なパッケージをロード library(ArrayExpress) #パッケージの読み込み library(affy) #パッケージの読み込み #前処理(データ取得) hoge <- ArrayExpress(param, save=F) #paramで指定したIDのCELファイルなどを取得した結果をhogeに格納 #本番 eset <- mas5(hoge) #MASを実行し、結果をesetに保存 #対数変換 summary(exprs(eset)) #得られたesetの遺伝子発現行列のシグナル強度分布を表示 exprs(eset) <- log(exprs(eset), 2) #底を2として対数変換 #ファイルに保存 write.exprs(eset, file=out_f) #結果を指定したファイル名で保存
正規化 | Affymetrix GeneChip | MBEI (Li_2001)
Affymetrix chip (GeneChipTM)を用いて得られた*.CELファイルを元に、MBEI(Li and Wong, PNAS, 2001)アルゴリズムを用いてSummary scoreを算出。
「ファイル」−「ディレクトリの変更」で適切なディレクトリに移動し以下をコピペ。
1. (CELファイルがあるディレクトリ上で)手元にあるCELファイルの読み込みから行う場合:
PM onlyモデルです。
out_f <- "hoge1.txt" #出力ファイル名を指定してout_fに格納 #必要なパッケージをロード library(affy) #パッケージの読み込み #データファイルの読み込み(*.CELファイル) hoge <- ReadAffy() #*.CELファイルの読み込み #本番 eset <- expresso(hoge, normalize.method="invariantset", bg.correct=FALSE,#dChip(PM onlyモデル)を実行し、結果をesetに保存 pmcorrect.method="pmonly", summary.method="liwong")#dChip(PM onlyモデル)を実行し、結果をesetに保存 #対数変換 summary(exprs(eset)) #得られたesetの遺伝子発現行列のシグナル強度分布を表示 exprs(eset)[exprs(eset) < 1] <- 1 #対数変換(log2)できるようにシグナル強度が1未満のものを1にしておく summary(exprs(eset)) #上記処理後のシグナル強度分布を再び表示させて確認 exprs(eset) <- log(exprs(eset), 2) #底を2として対数変換 #ファイルに保存 write.exprs(eset, file=out_f) #結果を指定したファイル名で保存
2. (CELファイルがあるディレクトリ上で)手元にあるCELファイルの読み込みから行う場合:
PM-MMモデルです。
out_f <- "hoge2.txt" #出力ファイル名を指定してout_fに格納 #必要なパッケージをロード library(affy) #パッケージの読み込み #データファイルの読み込み(*.CELファイル) hoge <- ReadAffy() #*.CELファイルの読み込み #本番 eset <- expresso(hoge, normalize.method="invariantset", bg.correct=FALSE,#dChip(PM-MMモデル)を実行し、結果をesetに保存 pmcorrect.method="subtractmm", summary.method="liwong")#dChip(PM-MMモデル)を実行し、結果をesetに保存 #対数変換 summary(exprs(eset)) #得られたesetの遺伝子発現行列のシグナル強度分布を表示 exprs(eset)[exprs(eset) < 1] <- 1 #対数変換(log2)できるようにシグナル強度が1未満のものを1にしておく summary(exprs(eset)) #上記処理後のシグナル強度分布を再び表示させて確認 exprs(eset) <- log(exprs(eset), 2) #底を2として対数変換 #ファイルに保存 write.exprs(eset, file=out_f) #結果を指定したファイル名で保存
3. AffymetrixデータGSE30533 (Kamei et al., PLoS One, 2013)のCELファイル取得から行う場合:
指定したGSE IDが複数種類のアレイで行われたCELファイルを含んでいたらうまくいかないかもしれません。
out_f <- "hoge3.txt" #出力ファイル名を指定してout_fに格納 param <- "GSE30533" #入手したいIDを指定 #必要なパッケージをロード library(ArrayExpress) #パッケージの読み込み library(affy) #パッケージの読み込み #前処理(データ取得) hoge <- ArrayExpress(param, save=F) #paramで指定したIDのCELファイルなどを取得した結果をhogeに格納 #本番 eset <- expresso(hoge, normalize.method="invariantset", bg.correct=FALSE,#dChip(PM-MMモデル)を実行し、結果をesetに保存 pmcorrect.method="subtractmm", summary.method="liwong")#dChip(PM-MMモデル)を実行し、結果をesetに保存 #対数変換 summary(exprs(eset)) #得られたesetの遺伝子発現行列のシグナル強度分布を表示 exprs(eset)[exprs(eset) < 1] <- 1 #対数変換(log2)できるようにシグナル強度が1未満のものを1にしておく summary(exprs(eset)) #上記処理後のシグナル強度分布を再び表示させて確認 exprs(eset) <- log(exprs(eset), 2) #底を2として対数変換 #ファイルに保存 write.exprs(eset, file=out_f) #結果を指定したファイル名で保存
前処理について
「スケーリング」については、既存の方法が対数変換後のデータを入力としている場合が多いため、もしそうなっていなければやります。 「フィルタリング」については、私の二群間比較用手法WAD (Kadota et al., 2008) がAUCでの評価を基本としていること、そして全体的に高発現な遺伝子ほど大きな重みを与えるという数式を基本としており、低発現遺伝子のフィルタリングを行うと結果がか えって歪む恐れがありそうだと思ったため私はやらないというのを基本としていました。
しかし、t検定のようなばらつきを計算して発現変動遺伝子(DEG)数を正確に見積もろうとする方法を用いる場合には、adjusted p-valueを求める際に全体の遺伝子数が関係してきます。 そして低発現遺伝子などのフィルタリングを行い遺伝子数を減らしておくことで、false discovery rate (FDR)など多重比較問題への対応(multiple testing adjustment)を行う際に結果に与える影響を減らすことができます。 これは、「1つ真のDEGのp-value = 0.002、non-DEGが999個」存在する状況と、予めnon-informative genesとしてフィルタリングしておき「1つ真のDEGのp-value = 0.002、non-DEGが9個」 であるときの単純な多重比較補正の一つであるBonferroni補正などを思い浮かべれば理解しやすいと思います。そのため、以下にフィルタリングを肯定的なものとした論文を中心にリストアップしておきます。
例えば、Talloen et al., 2007は二群間比較用データなどのフィルタリング時にクラスラベル情報 (どのサンプルがG1群でどれがG2群かなどの情報のこと)を使わないでフィルタリング(nonspecific or unsupervised filtering)すれば、そのあとに行う検定に影響を及ぼさないのでよいと述べています。 このようなnonspecific filteringには、ラベル情報を使わないサンプル全体での分散や平均に基づく統計量が用いられます(Bourgon et al., 2010)。 Affymetrix GeneChipデータ解析時にPresent/Absent callの情報を利用して、「全サンプルの50%以上でPresent callとなっているプローブセットのみをフィルタリングしました」的な手続きもnonspecific filterの範疇に含まれます。
- Marczyk et al., BMC Bioinformatics, 2013
- PVAC:Lu et al., Nucleic Acids Res., 2011
- Bourgon et al., PNAS, 2010
- Mieczkowski et al., BMC Bioinformatics, 2010
- Hackstadt and Hess, BMC Bioinformatics, 2009
- WAD:Kadota et al., Algorithms Mol. Biol., 2008
- FARMS:Talloen et al., Bioinformatics, 2007
- McClintick and Edenberg, BMC Bioinformatics, 2006
前処理 | スケーリング | サンプル間のシグナル強度の平均値をそろえる
よく論文中で各サンプル(各列)の発現データの平均をXにそろえて...などという記述があります。ここでは、二つの例題を示します。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動。
1. 10 genes × 2 samplesのデータファイル(sample19.txt)の場合:
in_f <- "sample19.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge.txt" #出力ファイル名を指定してout_fに格納 param <- 10 #各サンプルの正規化後の平均値を指定 #データファイルの読み込み data_tmp <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 tmp_mean <- apply(data_tmp, 2, mean, na.rm=TRUE)#各サンプル(列)の平均シグナル強度を計算した結果をtmp_meanに格納 data <- sweep(data_tmp, 2, param/tmp_mean, "*")#各列中の全てのシグナル値にparam/tmp_meanを掛け、その結果をdataに格納 data #結果を表示 apply(data, 2, mean) #各列のmeanを表示させ、正常に動作しているか確認 #ファイルに保存 tmp <- cbind(rownames(data), data) #遺伝子IDの列を行列dataの左端に挿入し、結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
2. 6 genes × 11 samplesのデータファイル(sample2.txt)の場合:
in_f <- "sample2.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge.txt" #出力ファイル名を指定してout_fに格納 param <- 100 #各サンプルの正規化後の平均値を指定 #データファイルの読み込み data_tmp <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 tmp_mean <- apply(data_tmp, 2, mean, na.rm=TRUE)#各サンプル(列)の平均シグナル強度を計算した結果をtmp_meanに格納 data <- sweep(data_tmp, 2, param/tmp_mean, "*")#各列中の全てのシグナル値にparam/tmp_meanを掛け、その結果をdataに格納 data #結果を表示 apply(data, 2, mean) #各列のmeanを表示させ、正常に動作しているか確認 #ファイルに保存 tmp <- cbind(rownames(data), data) #遺伝子IDの列を行列dataの左端に挿入し、結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
前処理 | スケーリング | サンプル間のシグナル強度の中央値をそろえる
よく論文中で各サンプル(各列)の発現データの中央値(median)をXにそろえて...などという記述があります。ここではX=50とした場合のやり方を例示します。
「ファイル」−「ディレクトリの変更」で解析したいファイル(sample2.txt)を置いてあるディレクトリに移動。
in_f <- "sample2.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge.txt" #出力ファイル名を指定してout_fに格納 param <- 50 #各サンプルの正規化後の中央値を指定 #データファイルの読み込み data_tmp <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み tmp_median <- apply(data_tmp, 2, median, na.rm=TRUE)#各サンプル(列)のシグナル強度のmedianを計算した結果をtmp_medianに格納 data <- sweep(data_tmp, 2, param/tmp_median, "*")#各列中の全てのシグナル値にparam/tmp_medianを掛け、その結果をdataに格納 data #結果を表示 apply(data, 2, median) #各列のmedianを表示させ、正常に動作しているか確認 #ファイルに保存 tmp <- cbind(rownames(data), data) #遺伝子IDの列を行列dataの左端に挿入し、結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
前処理 | スケーリング | 各サンプルのシグナル強度の平均を0、標準偏差を1にする
いわゆるZスケーリング(Zスコア化)というやつです。いくつかのやり方を例示しておきます。
「ファイル」−「ディレクトリの変更」で解析したいファイル(sample2.txt)を置いてあるディレクトリに移動し、以下をコピペ。
1. やり方1:
in_f <- "sample2.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge.txt" #出力ファイル名を指定してout_fに格納 #必要なパッケージをロード library(som) #パッケージの読み込み #データファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 data.z <- normalize(data, byrow=FALSE) #列方向に正規化した結果をdata.zに格納 data.z #結果を表示 apply(data.z, 2, mean) #各列のmeanを表示させ、正常に動作しているか確認 #ファイルに保存 tmp <- cbind(rownames(data.z), data.z) #遺伝子IDの列を行列data.zの左端に挿入し、結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
2. やり方2:
in_f <- "sample2.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge.txt" #出力ファイル名を指定してout_fに格納 #必要なパッケージをロード library(genefilter) #パッケージの読み込み #データファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 data.z <- genescale(data, axis=2, method="Z")#列方向に正規化した結果をdata.zに格納 data.z #結果を表示 apply(data.z, 2, mean) #各列のmeanを表示させ、正常に動作しているか確認 #ファイルに保存 tmp <- cbind(rownames(data.z), data.z) #遺伝子IDの列を行列data.zの左端に挿入し、結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
3. やり方3:
in_f <- "sample2.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge.txt" #出力ファイル名を指定してout_fに格納 #データファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.z <- scale(data) #列方向に正規化した結果をdata.zに格納 data.z #結果を表示 apply(data.z, 2, mean) #各列のmeanを表示させ、正常に動作しているか確認 #ファイルに保存 tmp <- cbind(rownames(data.z), data.z) #遺伝子IDの列を行列data.zの左端に挿入し、結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
前処理 | スケーリング | 各遺伝子のシグナル強度の平均を0、標準偏差を1にする
いわゆるZスケーリング(Zスコア化)というやつです。いくつかのやり方を例示しておきます。
「ファイル」−「ディレクトリの変更」で解析したいファイル(sample2.txt)を置いてあるディレクトリに移動し、以下をコピペ
1. やり方1:
in_f <- "sample2.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge.txt" #出力ファイル名を指定してout_fに格納 #必要なパッケージをロード library(som) #パッケージの読み込み #データファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 data.z <- normalize(data, byrow=TRUE) #行方向に正規化した結果をdata.zに格納 data.z #結果を表示 apply(data.z, 1, mean) #各行のmeanを表示させ、正常に動作しているか確認 #ファイルに保存 tmp <- cbind(rownames(data.z), data.z) #遺伝子IDの列を行列data.zの左端に挿入し、結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
2. やり方2:
in_f <- "sample2.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge.txt" #出力ファイル名を指定してout_fに格納 #必要なパッケージをロード library(genefilter) #パッケージの読み込み #データファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 data.z <- genescale(data, axis=1, method="Z")#行方向に正規化した結果をdata.zに格納 data.z #結果を表示 apply(data.z, 1, mean) #各行のmeanを表示させ、正常に動作しているか確認 #ファイルに保存 tmp <- cbind(rownames(data.z), data.z) #遺伝子IDの列を行列data.zの左端に挿入し、結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
3. やり方3:
in_f <- "sample2.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge.txt" #出力ファイル名を指定してout_fに格納 #データファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 tmp <- scale(t(data)) #scale関数は列方向のscalingしかしてくれないので、t関数を使って転置行列に対してscale関数を実行し、結果をtmpに格納 data.z <- t(tmp) #前の行で行列を転置させていたので、もう一度転置しなおした結果をdata.zに格納 data.z #結果を表示 apply(data.z, 1, mean) #各行のmeanを表示させ、正常に動作しているか確認 #ファイルに保存 tmp <- cbind(rownames(data.z), data.z) #遺伝子IDの列を行列data.zの左端に挿入し、結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
前処理 | スケーリング | 各サンプル or 遺伝子のシグナル強度の平均を0、MADを1にする
発現データを正規化(mean=0, MAD=1)してくれる。
「ファイル」−「ディレクトリの変更」で解析したい実数データのファイル(sample5.txt)を置いてあるディレクトリに移動。
1. 遺伝子(行)方向にスケーリングしたい場合:
in_f <- "sample5.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge.txt" #出力ファイル名を指定してout_fに格納 #データファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#入力ファイルを読み込んでdataに格納 #本番 data.t <- t(data) #行列の転置(この後に使うscale関数が列ごとの操作を行うため、scale関数をそのまま使えるように予め行列を入れ替えておく必要があるため) data.t.mean.mad <- scale(data.t, apply(data.t,2,mean), apply(data.t,2,mad,constant=1))#各列のmean=0, MAD=1になるようにスケーリングし、結果をdata.t.mean.madに格納 data.mean.mad <- t(data.t.mean.mad) #scale関数の適用が終わったので、もう一度行列の転置を行って元に戻し、結果をdata.mean.madに格納 apply(data.mean.mad, 1, mean) #各行のmeanを表示させ、正常に動作しているか確認 #ファイルに保存 tmp <- cbind(rownames(data.mean.mad), data.mean.mad)#遺伝子IDの列を行列data.mean.madの左端に挿入し、結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
2. サンプル(列)方向にスケーリングしたい場合:
in_f <- "sample5.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge.txt" #出力ファイル名を指定してout_fに格納 #データファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 data.mean.mad <- scale(data, apply(data,2,mean), apply(data,2,mad,constant=1))#各列のmean=0, MAD=1になるようにスケーリングし、結果をdata.mean.madに格納 apply(data.mean.mad, 2, mean) #各列のmeanを表示させ、正常に動作しているか確認 #ファイルに保存 tmp <- cbind(rownames(data.mean.mad), data.mean.mad)#遺伝子IDの列を行列data.mean.madの左端に挿入し、結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
前処理 | スケーリング | 各サンプル or 遺伝子のシグナル強度の中央値を0、標準偏差を1にする
発現データを正規化(median=0, standard deviation (SD)=1)してくれる。
「ファイル」−「ディレクトリの変更」で解析したい実数データのファイル(sample5.txt)を置いてあるディレクトリに移動。
1. 遺伝子(行)方向にスケーリングしたい場合:
in_f <- "sample5.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge.txt" #出力ファイル名を指定してout_fに格納 #データファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 data.t <- t(data) #行列の転置(この後に使うscale関数が列ごとの操作を行うため、scale関数をそのまま使えるように予め行列を入れ替えておく必要があるため) data.t.m.sd <- scale(data.t, apply(data.t,2,median), apply(data.t,2,sd))#各列のmedian=0, SD=1になるようにスケーリングし、結果をdata.t.m.sdに格納 data.m.sd <- t(data.t.m.sd) #scale関数の適用が終わったので、もう一度行列の転置を行って元に戻し、結果をdata.m.sdに格納 apply(data.m.sd, 1, median) #各行のmedianを表示させ、正常に動作しているか確認 #ファイルに保存 tmp <- cbind(rownames(data.m.sd), data.m.sd)#遺伝子IDの列を行列data.m.sdの左端に挿入し、結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
2. サンプル(列)方向にスケーリングしたい場合:
in_f <- "sample5.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge.txt" #出力ファイル名を指定してout_fに格納 #データファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 data.m.sd <- scale(data, apply(data,2,median), apply(data,2,sd))#各列のmedian=0, SD=1になるようにスケーリングし、結果をdata.m.sdに格納 apply(data.m.sd, 2, median) #各列のmedianを表示させ、正常に動作しているか確認 #ファイルに保存 tmp <- cbind(rownames(data.m.sd), data.m.sd)#遺伝子IDの列を行列data.m.sdの左端に挿入し、結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
前処理 | スケーリング | 各サンプル or 遺伝子のシグナル強度の中央値を0、MADを1にする
発現データを正規化(median=0、Median Absolute Deviation (MAD)=1)してくれる。
「ファイル」−「ディレクトリの変更」で解析したいファイル(sample5.txt)を置いてあるディレクトリに移動。
1. 遺伝子(行)方向にスケーリングしたい場合:
in_f <- "sample5.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge.txt" #出力ファイル名を指定してout_fに格納 #データファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 data.t <- t(data) #行列の転置(この後に使うscale関数が列ごとの操作を行うため、scale関数をそのまま使えるように予め行列を入れ替えておく必要があるため) data.t.m.mad <- scale(data.t, apply(data.t,2,median), apply(data.t,2,mad,constant=1))#各列のmedian=0, MAD=1になるようにスケーリングし、結果をdata.t.m.madに格納 data.m.mad <- t(data.t.m.mad) #scale関数の適用が終わったので、もう一度行列の転置を行って元に戻し、結果をdata.m.madに格納 apply(data.m.mad, 1, median) #各行のmedianを表示させ、正常に動作しているか確認 #ファイルに保存 tmp <- cbind(rownames(data.m.mad), data.m.mad)#遺伝子IDの列を行列data.m.madの左端に挿入し、結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
2. サンプル(列)方向にスケーリングしたい場合:
in_f <- "sample5.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge.txt" #出力ファイル名を指定してout_fに格納 #データファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 data.m.mad <- scale(data, apply(data,2,median), apply(data,2,mad,constant=1))#各列のmedian=0, MAD=1になるようにスケーリングし、結果をdata.m.madに格納 apply(data.m.mad, 2, median) #各列のmedianを表示させ、正常に動作しているか確認 #ファイルに保存 tmp <- cbind(rownames(data.m.mad), data.m.mad)#遺伝子IDの列を行列data.m.madの左端に挿入し、結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
前処理 | スケーリング | 各サンプル or 遺伝子のシグナル強度のTukey biweightを0、MADを1にする
発現データを正規化(Tukey's biweight=0、Median Absolute Deviation (MAD)=1)してくれる。
「ファイル」−「ディレクトリの変更」で解析したいファイル(sample5.txt)を置いてあるディレクトリに移動。
1. 遺伝子(行)方向にスケーリングしたい場合:
in_f <- "sample5.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge.txt" #出力ファイル名を指定してout_fに格納 #必要なパッケージをロード library(affy) #tukey.biweight関数が含まれているaffyパッケージの読み込み #データファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 data.t <- t(data) #行列の転置(この後に使うscale関数が列ごとの操作を行うため、scale関数をそのまま使えるように予め行列を入れ替えておく必要があるため) data.t.tukey.mad <- scale(data.t,apply(data.t,2,tukey.biweight),apply(data.t,2,mad,constant=1))#各列のTukey's biweight=0, MAD=1になるようにスケーリングし、結果をdata.t.tukey.madに格納 data.tukey.mad <- t(data.t.tukey.mad) #scale関数の適用が終わったので、もう一度行列の転置を行って元に戻し、結果をdata.tukey.madに格納 apply(data.tukey.mad, 1, tukey.biweight)#各行のTukey's biweightを表示させ、正常に動作しているか確認 #ファイルに保存 tmp <- cbind(rownames(data.tukey.mad), data.tukey.mad)#遺伝子IDの列を行列data.tukey.madの左端に挿入し、結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
2. サンプル(列)方向にスケーリングしたい場合:
in_f <- "sample5.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge.txt" #出力ファイル名を指定してout_fに格納 #必要なパッケージをロード library(affy) #tukey.biweight関数が含まれているaffyパッケージの読み込み #データファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#入力ファイルを読み込んでdataに格納 data.tukey.mad <- scale(data,apply(data,2,tukey.biweight), apply(data,2,mad,constant=1))#各列のTukey's biweight=0, MAD=1になるようにスケーリングし、結果をdata.tukey.madに格納 apply(data.tukey.mad, 2, tukey.biweight)#各列のTukey's biweightを表示させ、正常に動作しているか確認 #ファイルに保存 tmp <- cbind(rownames(data.tukey.mad), data.tukey.mad)#遺伝子IDの列を行列data.tukey.madの左端に挿入し、結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
前処理 | スケーリング | 各サンプル or 遺伝子のシグナル強度の範囲を0-1にする
「ファイル」−「ディレクトリの変更」で解析したいファイル(sample2.txt)を置いてあるディレクトリに移動し、以下をコピペ
遺伝子(行)方向にスケーリングしたい場合:
in_f <- "sample2.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge.txt" #出力ファイル名を指定してout_fに格納 #必要なパッケージをロード library(genefilter) #パッケージの読み込み #データファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 data.r <- genescale(data, axis=1, method="R")#スケーリングした結果をdata.rに格納 apply(data.r, 1, range) #各行の最小値と最大値を表示させ、正常に動作しているか確認 #ファイルに保存 tmp <- cbind(rownames(data.r), data.r) #遺伝子IDの列を行列data.rの左端に挿入し、結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
サンプル(列)方向にスケーリングしたい場合:
in_f <- "sample2.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge.txt" #出力ファイル名を指定してout_fに格納 #必要なパッケージをロード library(genefilter) #パッケージの読み込み #データファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 data.r <- genescale(data, axis=2, method="R")#スケーリングした結果をdata.rに格納 apply(data.r, 2, range) #各列の最小値と最大値を表示させ、正常に動作しているか確認 #ファイルに保存 tmp <- cbind(rownames(data.r), data.r) #遺伝子IDの列を行列data.rの左端に挿入し、結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
前処理 | スケーリング | シグナル強度を対数(log)変換する
発現データを対数(log)変換してくれます。ほぼ例外なく底は2なので、ここではそのやり方のみ示します。
尚、予め「シグナル強度が1未満のものを1にする」ということを行っていますが、これはlogをとれるようにするためです。実際にWADのKadota et al., 2008中で以下のような操作を行っています。
くれぐれもご自身が対数変換しようとしている入力ファイルについて、「シグナル強度の分布を確認し、ダイナミックレンジが4桁程度あることを確認」してください。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し、以下をコピペ
1. sample2.txtのようなごく一般的な形式のファイルをlog変換したいとき:
in_f <- "sample2.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge1.txt" #出力ファイル名を指定してout_fに格納 #データファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 summary(data) #シグナル強度の分布を確認し、ダイナミックレンジが4桁程度あることを確認 data[data < 1] <- 1 #シグナル強度が1未満のものを1にする data.log <- log(data, base=2) #log2-transformed dataをdata.logに格納 summary(data.log) #対数変換後のシグナル強度の分布を確認 #ファイルに保存 tmp <- cbind(rownames(data.log), data.log)#遺伝子IDの列を行列data.logの左端に挿入し、結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
2. GDS1096.txtのような"IDENTIFIER"という余分な一列を含むファイルを処理したいとき:
in_f <- "GDS1096.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge2.txt" #出力ファイル名を指定してout_fに格納 #データファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data$IDENTIFIER <- NULL #余分なIDENTIFIER列の消去 summary(data) #シグナル強度の分布を確認し、ダイナミックレンジが4桁程度あることを確認 #本番 data[data < 1] <- 1 #シグナル強度が1未満のものを1にする data.log <- log(data, base=2) #log2-transformed dataをdata.logに格納 summary(data.log) #対数変換後のシグナル強度の分布を確認 #ファイルに保存 tmp <- cbind(rownames(data.log), data.log)#遺伝子IDの列を行列data.logの左端に挿入し、結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
前処理 | スケーリング | Quantile normalization
発現データをQuantile normalization(発現強度の順位が同じならその発現強度も同じにする正規化)してくれます。 Jeffery et al., 2006の解析で行われた前処理と同じ(RMA-quantified data -> Quantile正規化)です。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し、以下をコピペ
1. sample5.txtの場合:
in_f <- "sample5.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge1.txt" #出力ファイル名を指定してout_fに格納 #必要なパッケージをロード library(limma) #パッケージの読み込み #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 data.q <- normalizeBetweenArrays(as.matrix(data))#Quantile正規化を実行し、結果をdata.qに格納 #ファイルに保存 tmp <- cbind(rownames(data.q), data.q) #遺伝子IDの列を行列data.qの左端に挿入し、結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
2. sample19.txtの場合:
in_f <- "sample19.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge2.txt" #出力ファイル名を指定してout_fに格納 #必要なパッケージをロード library(limma) #パッケージの読み込み #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 data.q <- normalizeBetweenArrays(as.matrix(data))#Quantile正規化を実行し、結果をdata.qに格納 #ファイルに保存 tmp <- cbind(rownames(data.q), data.q) #遺伝子IDの列を行列data.qの左端に挿入し、結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
3. sample19_plus1.txtの場合:
in_f <- "sample19_plus1.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge3.txt" #出力ファイル名を指定してout_fに格納 #必要なパッケージをロード library(limma) #パッケージの読み込み #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 data.q <- normalizeBetweenArrays(as.matrix(data))#Quantile正規化を実行し、結果をdata.qに格納 #ファイルに保存 tmp <- cbind(rownames(data.q), data.q) #遺伝子IDの列を行列data.qの左端に挿入し、結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
前処理 | フィルタリング | 低発現遺伝子を除去
特定の条件を満たす遺伝子のみを抽出(フィルタリング;filtering)するやり方(特に低発現遺伝子の除去)を示します。サンプルのラベル情報を見ていないのでnonspecific filteringの一つです。
注意点としては「フィルタリングしようとしているデータが対数変換(or log変換)されているかどうかをちゃんと把握しておく」ことが大事です。以下の解析例で用いているsample2.txtは対数変換前のデータなので、解析例1で行っているような「シグナル強度50以上」という条件を満たす遺伝子が存在します。
しかし、もしこれと同じことを対数変換後のデータで行おうとすると、一般にシグナル強度が250 (=1.1259e+15)を超えるような途方もなく大きな数値を出すような機器は存在しないので、条件を満たす遺伝子が存在しないことになります。だからその後の解析で何をやってもエラーが出力されるのです。このあたりに注意して利用してください。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し、以下をコピペ
1. サンプルデータ2のsample2.txtの場合:
6 genes×11 samplesからなる二群の遺伝子発現データ。最初の6サンプルがG1群、残りの5サンプルがG2群のデータです。
5組織(k=5)以上でシグナル強度50以上(A=50)の遺伝子のみを抽出するやり方です。
in_f <- "sample2.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge1.txt" #出力ファイル名を指定してout_fに格納 param1 <- 5 #組織数kを指定 param2 <- 50 #シグナル強度Aを指定 #必要なパッケージをロード library(genefilter) #パッケージの読み込み #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 f1 <- kOverA(param1, A=param2) #「k組織以上でシグナル強度A以上を持つ遺伝子を抽出」という条件(filter)をf1に格納 ffun <- filterfun(f1) #フィルタリング用の関数(filtering function)を作成しffunに格納 obj <- genefilter(data, ffun) #条件を満たすかどうかを判定した結果をobjに格納 obj #確認してるだけです data <- data[obj,] #objがTRUEとなる要素のみ抽出した結果をdataに格納 data #確認してるだけです #ファイルに保存 tmp <- cbind(rownames(data), data) #保存したい情報をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
2. サンプルデータ2のsample2.txtの場合:
6 genes×11 samplesからなる二群の遺伝子発現データ。最初の6サンプルがG1群、残りの5サンプルがG2群のデータです。
シグナル強度 > 20(A=20)の組織数の割合が > 70%(p=0.7)を満たす遺伝子のみを抽出するやり方です。
in_f <- "sample2.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge2.txt" #出力ファイル名を指定してout_fに格納 param1 <- 0.7 #組織数の割合pを指定 param2 <- 20 #シグナル強度Aを指定 #必要なパッケージをロード library(genefilter) #パッケージの読み込み #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 f1 <- pOverA(p=param1, A=param2) #「シグナル強度がAよりも大きい組織数の割合がpよりも大きい遺伝子を抽出」という条件(filter)をf1に格納 ffun <- filterfun(f1) #フィルタリング用の関数(filtering function)を作成しffunに格納 obj <- genefilter(data, ffun) #条件を満たすかどうかを判定した結果をobjに格納 obj #確認してるだけです data <- data[obj,] #objがTRUEとなる要素のみ抽出した結果をdataに格納 data #確認してるだけです #ファイルに保存 tmp <- cbind(rownames(data), data) #保存したい情報をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
3. サンプルデータ2のsample2.txtの場合:
6 genes×11 samplesからなる二群の遺伝子発現データ。最初の6サンプルがG1群、残りの5サンプルがG2群のデータです。
少なくとも一つの組織でシグナル強度が92(A=92)以上の遺伝子を抽出するやり方です。
in_f <- "sample2.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge3.txt" #出力ファイル名を指定してout_fに格納 param <- 92 #シグナル強度Aを指定 #必要なパッケージをロード library(genefilter) #パッケージの読み込み #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 f1 <- maxA(param) #「少なくとも一つの組織でシグナル強度がparam以上の遺伝子を抽出」という条件(filter)をf1に格納 ffun <- filterfun(f1) #フィルタリング用の関数(filtering function)を作成しffunに格納 obj <- genefilter(data, ffun) #条件を満たすかどうかを判定した結果をobjに格納 obj #確認してるだけです data <- data[obj,] #objがTRUEとなる要素のみ抽出した結果をdataに格納 data #確認してるだけです #ファイルに保存 tmp <- cbind(rownames(data), data) #保存したい情報をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
4. サンプルデータ22のsample22.txtの場合:
10,000 genes×6 samplesからなる二群の遺伝子発現データ。最初の3サンプルがG1群、残りの3サンプルがG2群の標準正規分布に従う乱数からなるシミュレーションデータです。 乱数を発生させただけのデータなので、発現変動遺伝子(DEG)がない全てがnon-DEGのデータです。
平均シグナル強度が下位10%未満の遺伝子を除去するやり方です。
Bourgon et al., 2010のFig. 1B (Filtering on overall mean)のtheta = 10%に相当するフィルタリングです。
in_f <- "sample22.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge4.txt" #出力ファイル名を指定してout_fに格納 param <- 0.1 #フィルタリングしたい下位x%を指定 #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 ave <- rowMeans(data) #行ごとの平均値を算出した結果をaveに格納 hoge <- quantile(ave, probs=param) #paramで指定した下位の位置情報をhogeに格納 obj <- (ave >= hoge) #条件を満たすかどうかを判定した結果をobjに格納 data <- data[obj,] #objがTRUEとなる要素のみ抽出した結果をdataに格納 dim(data) #確認してるだけです #ファイルに保存 tmp <- cbind(rownames(data), data) #保存したい情報をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
前処理 | フィルタリング | log比が小さいものを除去
特定の条件を満たす遺伝子のみを抽出(フィルタリング;filtering)するやり方(特にlog比が小さいものを除去)を示します。サンプルのラベル情報を見ていないのでnonspecific filteringの一つです。
注意点としては「フィルタリングしようとしているデータが対数変換(or log変換)されているかどうかをちゃんと把握しておく」ことが大事です。 以下の解析例で用いているsample2.txtは対数変換されていないデータなので、以下の条件を満たす遺伝子が存在します。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し、以下をコピペ
1. サンプルデータ2のsample2.txtの場合:
6 genes×11 samplesからなる二群の遺伝子発現データ。最初の6サンプルがG1群、残りの5サンプルがG2群のデータです。
「発現強度max/min < 2.9」の行(遺伝子)を解析から除くやり方です。
in_f <- "sample2.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge1.txt" #出力ファイル名を指定してout_fに格納 param <- 2.9 #シグナル強度最大と最小の発現比を指定 #必要なパッケージをロード library(som) #パッケージの読み込み #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 data <- filtering(data,lt=min(data),ut=max(data),mmr=param,mmd=0)#フィルタリングを実行し、結果をdataに格納 data #確認してるだけです #ファイルに保存 tmp <- cbind(rownames(data), data) #保存したい情報をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
2. サンプルデータ2のsample2.txtの場合:
6 genes×11 samplesからなる二群の遺伝子発現データ。最初の6サンプルがG1群、残りの5サンプルがG2群のデータです。
「発現強度max/min < 2.9」または「(max-min) < 42」の行(遺伝子)を解析から除くやり方です。
in_f <- "sample2.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge2.txt" #出力ファイル名を指定してout_fに格納 param1 <- 10 #シグナル強度の下限を指定 param2 <- 100 #シグナル強度の上限を指定 param3 <- 2.9 #シグナル強度最大と最小の発現比を指定 param4 <- 42 #シグナル強度最大と最小の差を指定 #必要なパッケージをロード library(som) #パッケージの読み込み #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 data <- filtering(data, lt=param1, ut=param2, mmr=param3, mmd=param4)#フィルタリングを実行し、結果をdataに格納 data #確認してるだけです #ファイルに保存 tmp <- cbind(rownames(data), data) #保存したい情報をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
3. サンプルデータ14のsample14.txtの場合:
22,283 genes×6 samplesからなる二群の遺伝子発現データ。最初の3サンプルがG1群、残りの3サンプルがG2群のデータです。
対数変換後(base=2; 底は2)のデータです。
「発現強度max/min < 2.0」の行(遺伝子)を解析から除くやり方です。|log(max/min)| < 1の遺伝子の除去に相当します。
in_f <- "sample14.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge3.txt" #出力ファイル名を指定してout_fに格納 param <- 2.0 #シグナル強度最大と最小の発現比を指定(対数変換前の値) #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 max <- apply(data, 1, max) #行ごとのシグナル強度の最大値をmaxに格納 min <- apply(data, 1, min) #行ごとのシグナル強度の最小値をminに格納 logratio <- max - min #フィルタリングを実行した結果をobjに格納 obj <- (logratio >= log2(param)) #条件を満たすかどうかを判定した結果をobjに格納 data <- data[obj,] #objがTRUEとなる要素のみ抽出した結果をdataに格納 summary(logratio) #確認してるだけです dim(data) #確認してるだけです #ファイルに保存 tmp <- cbind(rownames(data), data) #保存したい情報をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
4. サンプルデータ14のsample14.txtの場合:
22,283 genes×6 samplesからなる二群の遺伝子発現データ。最初の3サンプルがG1群、残りの3サンプルがG2群のデータです。
対数変換後(base=2; 底は2)のデータです。
log2(max/min)の絶対値が下位10%未満の遺伝子を除去するやり方です。
in_f <- "sample14.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge4.txt" #出力ファイル名を指定してout_fに格納 param <- 0.1 #フィルタリングしたい下位x%を指定 #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 max <- apply(data, 1, max) #行ごとのシグナル強度の最大値をmaxに格納 min <- apply(data, 1, min) #行ごとのシグナル強度の最小値をminに格納 logratio <- max - min #フィルタリングを実行した結果をobjに格納 hoge <- quantile(logratio, probs=param)#paramで指定した下位の位置情報をhogeに格納 obj <- (logratio >= hoge) #条件を満たすかどうかを判定した結果をobjに格納 data <- data[obj,] #objがTRUEとなる要素のみ抽出した結果をdataに格納 summary(logratio) #確認してるだけです dim(data) #確認してるだけです #ファイルに保存 tmp <- cbind(rownames(data), data) #保存したい情報をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
前処理 | フィルタリング | NAを含むものを除去
サンプルデータ13の(two-color) Agilentデータ(sample13_7vs7.txt)をエクセルで開くと多くの"NA" (Not Availableの略)という記述を目にしますが、 このような数値でない情報を含むデータは往々にしてうまくデータを読み込んでくれなかったり、解析できなかったりします...。ここでは全ての要素がNAとなっている行を除くなどのやり方を紹介します。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し、以下をコピペ
1. サンプルデータ13の(two-color) Agilentデータ(sample13_7vs7.txt)の場合:
22,575 genes×14 samplesからなる二群の遺伝子発現データ。最初の7列がG1群、後の7列がG2群の2群間比較用のデータです。
全ての要素がNAとなっている行を除くやり方1です。
in_f <- "sample13_7vs7.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge1.txt" #出力ファイル名を指定してout_fに格納 #必要なパッケージをロード library(genefilter) #パッケージの読み込み #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 obj <- apply(data, 1, allNA) #条件を満たすかどうかを判定した結果をobjに格納(全ての要素がNAならFALSE,それ以外ならTRUE) data <- data[obj,] #objがTRUEとなる要素のみ抽出した結果をdataに格納 dim(data) #確認してるだけです #ファイルに保存 tmp <- cbind(rownames(data), data) #保存したい情報をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
2. サンプルデータ13の(two-color) Agilentデータ(sample13_7vs7.txt)の場合:
22,575 genes×14 samplesからなる二群の遺伝子発現データ。最初の7列がG1群、後の7列がG2群の2群間比較用のデータです。
全ての要素がNAとなっている行を除くやり方2です。
in_f <- "sample13_7vs7.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge2.txt" #出力ファイル名を指定してout_fに格納 #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 hoge <- t(apply(data, 1, is.na)) #各要素がNAであるかどうか(TRUE or FALSE)を返すis.na関数を各行に対して適用した結果をhogeに格納 hoge2 <- apply(hoge, 1, sum) #TRUEの数(NAの数)を返すsum関数を各行に対して適用し、結果をhoge2に格納 obj <- hoge2 < ncol(data) #条件を満たすかどうかを判定した結果をobjに格納 data <- data[obj,] #objがTRUEとなる要素のみ抽出した結果をdataに格納 dim(data) #確認してるだけです #ファイルに保存 tmp <- cbind(rownames(data), data) #保存したい情報をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
3. サンプルデータ13の(two-color) Agilentデータ(sample13_7vs7.txt)の場合:
22,575 genes×14 samplesからなる二群の遺伝子発現データ。最初の7列がG1群、後の7列がG2群の2群間比較用のデータです。
一つでもNAがある行を除くやり方です。
in_f <- "sample13_7vs7.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge3.txt" #出力ファイル名を指定してout_fに格納 #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 hoge <- t(apply(data, 1, is.na)) #各要素がNAであるかどうか(TRUE or FALSE)を返すis.na関数を各行に対して適用した結果をhogeに格納 hoge2 <- apply(hoge, 1, sum) #TRUEの数(NAの数)を返すsum関数を各行に対して適用し、結果をhoge2に格納 obj <- (hoge2 == 0) #条件を満たすかどうかを判定した結果をobjに格納 data <- data[obj,] #objがTRUEとなる要素のみ抽出した結果をdataに格納 dim(data) #確認してるだけです #ファイルに保存 tmp <- cbind(rownames(data), data) #保存したい情報をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
4. サンプルデータ13の(two-color) Agilentデータ(sample13_7vs7.txt)の場合:
22,575 genes×14 samplesからなる二群の遺伝子発現データ。最初の7列がG1群、後の7列がG2群の2群間比較用のデータです。
「G1群で5個以上且つG2群で3個以上」のNAを含む行を除去するやり方です。
in_f <- "sample13_7vs7.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge4.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 7 #G1群のサンプル数を指定 param_G2 <- 7 #G2群のサンプル数を指定 param1 <- 5 #G1群のNA数の閾値を指定 param2 <- 3 #G2群のNA数の閾値を指定 #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #前処理(NAの要素数を各行についてカウント)と本番 hoge <- t(apply(data[data.cl==1],1,is.na))#各要素がNAであるかどうかを返すis.na関数をG1群のみに対して適用した結果をhogeに格納 obj1 <- apply(hoge,1,sum) < param1 #条件を満たすかどうかを判定した結果をobj1に格納(G1群) hoge <- t(apply(data[data.cl==2],1,is.na))#各要素がNAであるかどうかを返すis.na関数をG2群のみに対して適用した結果をhogeに格納 obj2 <- apply(hoge,1,sum) < param2 #条件を満たすかどうかを判定した結果をobj2に格納(G2群) obj <- (obj1 & obj2) #条件を満たすかどうかを判定した結果をobjに格納 data <- data[obj,] #objがTRUEとなる要素のみ抽出した結果をdataに格納 dim(data) #確認してるだけです #ファイルに保存 tmp <- cbind(rownames(data), data) #保存したい情報をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
前処理 | フィルタリング | CVが小さいものを除去
変動係数(Coefficient of Variation; CV)が閾値未満の遺伝子(行)を削除するやり方を示します。
変動係数は「標準偏差/平均」のことです。この値が大きい遺伝子(行)ほどバラツキ(正確には平均値に対する相対的なばらつき)がほうが大きいことを表すので、 全体的に発現変動していないものをフィルタリングする手段としておそらく誰かが利用していると思います。(利用している原著論文みつけたらPubmed ID教えてください。)
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し、以下をコピペ
1. サンプルデータ14のsample14.txtの場合:
22,283 genes×6 samplesからなる二群の遺伝子発現データ。最初の3サンプルがG1群、残りの3サンプルがG2群のデータです。
対数変換後(base=2; 底は2)のデータです。genefilterパッケージを利用するやり方です。
CVが0.2未満の遺伝子を除去するやり方です。
in_f <- "sample14.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge1.txt" #出力ファイル名を指定してout_fに格納 param <- 0.2 #CVの閾値を指定 #必要なパッケージをロード library(genefilter) #パッケージの読み込み #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 obj <- genefilter(data, cv(param, Inf))#条件を満たすかどうかを判定した結果をobjに格納 data <- data[obj,] #objがTRUEとなる要素のみ抽出した結果をdataに格納 dim(data) #確認してるだけです #ファイルに保存 tmp <- cbind(rownames(data), data) #保存したい情報をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
2. サンプルデータ14のsample14.txtの場合:
22,283 genes×6 samplesからなる二群の遺伝子発現データ。最初の3サンプルがG1群、残りの3サンプルがG2群のデータです。
対数変換後(base=2; 底は2)のデータです。genefilterパッケージを利用しないやり方です。
CVが0.2未満の遺伝子を除去するやり方です。
in_f <- "sample14.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge2.txt" #出力ファイル名を指定してout_fに格納 param <- 0.2 #CVの閾値を指定 #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 hoge <- apply(data,1,sd)/apply(data,1,mean)#CVを計算した結果をhogeに格納 obj <- (hoge >= param) #条件を満たすかどうかを判定した結果をobjに格納 data <- data[obj,] #objがTRUEとなる要素のみ抽出した結果をdataに格納 dim(data) #確認してるだけです #ファイルに保存 tmp <- cbind(rownames(data), data) #保存したい情報をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
3. サンプルデータ14のsample14.txtの場合:
22,283 genes×6 samplesからなる二群の遺伝子発現データ。最初の3サンプルがG1群、残りの3サンプルがG2群のデータです。
対数変換後(base=2; 底は2)のデータです。genefilterパッケージを利用しないやり方です。
CV値が下位10%未満の遺伝子を除去するやり方です。
in_f <- "sample14.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge3.txt" #出力ファイル名を指定してout_fに格納 param <- 0.1 #フィルタリングしたい下位x%を指定 #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 hoge <- apply(data,1,sd)/apply(data,1,mean)#CVを計算した結果をhogeに格納 hoge2 <- quantile(hoge, probs=param) #paramで指定した下位の位置情報をhogeに格納 obj <- (hoge >= hoge2) #条件を満たすかどうかを判定した結果をobjに格納 data <- data[obj,] #objがTRUEとなる要素のみ抽出した結果をdataに格納 summary(hoge) #確認してるだけです dim(data) #確認してるだけです #ファイルに保存 tmp <- cbind(rownames(data), data) #保存したい情報をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
前処理 | フィルタリング | 分散が小さいものを除去
分散(Variance)が閾値未満の遺伝子(行)を削除するやり方を示します。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し、以下をコピペ
1. サンプルデータ14のsample14.txtの場合:
22,283 genes×6 samplesからなる二群の遺伝子発現データ。最初の3サンプルがG1群、残りの3サンプルがG2群のデータです。
分散が0.2未満の遺伝子を除去するやり方です。
in_f <- "sample14.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge1.txt" #出力ファイル名を指定してout_fに格納 param <- 0.2 #閾値を指定 #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 hoge <- apply(data, 1, var) #分散を計算した結果をhogeに格納 obj <- (hoge >= param) #条件を満たすかどうかを判定した結果をobjに格納 data <- data[obj,] #objがTRUEとなる要素のみ抽出した結果をdataに格納 summary(hoge) #確認してるだけです dim(data) #確認してるだけです #ファイルに保存 tmp <- cbind(rownames(data), data) #保存したい情報をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
2. サンプルデータ14のsample14.txtの場合:
22,283 genes×6 samplesからなる二群の遺伝子発現データ。最初の3サンプルがG1群、残りの3サンプルがG2群のデータです。
分散が下位10%未満の遺伝子を除去するやり方です。
Bourgon et al., 2010のFig. 1A (Filtering on overall variance)のtheta = 10%に相当するフィルタリングです。
in_f <- "sample14.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge2.txt" #出力ファイル名を指定してout_fに格納 param <- 0.1 #フィルタリングしたい下位x%を指定 #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 hoge <- apply(data, 1, var) #分散を計算した結果をhogeに格納 hoge2 <- quantile(hoge, probs=param) #paramで指定した下位の位置情報をhogeに格納 obj <- (hoge >= hoge2) #条件を満たすかどうかを判定した結果をobjに格納 data <- data[obj,] #objがTRUEとなる要素のみ抽出した結果をdataに格納 summary(hoge) #確認してるだけです dim(data) #確認してるだけです #ファイルに保存 tmp <- cbind(rownames(data), data) #保存したい情報をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
3. サンプルデータ20のdata_rma_2_BAT.txtの場合:
31,099 probesets×8 samplesからなる二群の遺伝子発現データ。最初の4サンプルがG1群、残りの4サンプルがG2群のデータです。
分散が下位20%未満の遺伝子を除去するやり方です。
Bourgon et al., 2010のFig. 1A (Filtering on overall variance)のtheta = 20%に相当するフィルタリングです。
in_f <- "data_rma_2_BAT.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge3.txt" #出力ファイル名を指定してout_fに格納 param <- 0.2 #フィルタリングしたい下位x%を指定 #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 hoge <- apply(data, 1, var) #分散を計算した結果をhogeに格納 hoge2 <- quantile(hoge, probs=param) #paramで指定した下位の位置情報をhogeに格納 obj <- (hoge >= hoge2) #条件を満たすかどうかを判定した結果をobjに格納 data <- data[obj,] #objがTRUEとなる要素のみ抽出した結果をdataに格納 summary(hoge) #確認してるだけです dim(data) #確認してるだけです #ファイルに保存 tmp <- cbind(rownames(data), data) #保存したい情報をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
前処理 | ID変換 | について
例えば、「酸化的リン酸化」のパスウェイに関連する遺伝子セットが自分が見ている条件間で全体として動いているかどうかを調べたい場合に、 解析 | 機能解析 | 遺伝子オントロジー(GO)解析 | についてや解析 | 機能解析 | パスウェイ(Pathway)解析 | について で述べている方法を利用しますが、これを実行するための入力ファイルを作成する必要があります。 そのため、「酸化的リン酸化」のパスウェイに関連する遺伝子セット中の特定の遺伝子(遺伝子A)が自分が見ている条件間で発現変動していて、 しかもチップ上に重複して多数(別のプローブIDとして)搭載されているような場合には、遺伝子Aだけの効果でそのパスウェイが「動いている」などという誤った結果を導きかねません。 このようなチップ上の重複遺伝子の効果を排除すべく、同じ遺伝子名(gene symbolやEntrez ID)をもつ複数のプローブIDの発現プロファイルに対しては、 その代表値(平均値(mean)や中央値(median)など)を出力して、 遺伝子名の重複のない(non-redundant)遺伝子発現行列で解析を行うのが一般的です。
non-redundantにするためには、プローブIDとgene symbolやEntrez Gene IDなどの対応表(アノテーション情報)が必要になります。 この情報はイントロ | アノテーション情報取得 | GEOquery(Davis_2007)の3を行って得られた hoge3_GPL1355.txtのような形式の対応表ファイルを利用する戦略や、 Pathviewパッケージ(Luo et al., 2013)中のID変換用関数などを利用する戦略があります。 これらは内部的にアノテーションパッケージを利用します。Affymetrix, Agilent, Illumina製など数多くの製品(約200 chips)があります。 利用可能なパッケージ名については、全パッケージリスト(All Packages)中の ChipNameをご覧ください。
例えばNakai et al., BBB, 2008で用いられた 「Affymetrix Rat Genome 230 2.0 Array」のアノテーション情報はrat2302.dbパッケージから取得可能です。 これらのアノテーションパッケージはデフォルトではインストールされていません。そのため下記のようにしてインストールする必要があります。
param1 <- "rat2302.db" #パッケージ名を指定 #必要なパッケージのインストール source("http://bioconductor.org/biocLite.R")#指定したパッケージのインストール biocLite(param1, suppressUpdates=TRUE) #指定したパッケージのインストール
また、パッケージごとに利用可能なアノテーション情報は異なります。param2で指定可能なアノテーション情報は、keytypes関数実行結果で表示されているもののみとなりますのでご注意ください。
概ね、SYMBOL", "ENTREZID", "ACCNUM", "REFSEQ", "UNIGENE", "ENSEMBL", "ENSEMBLPROT", "ENSEMBLTRANS", "GENENAME", "PFAM", "PROSITE"などは利用可能です。 私の経験上、"REFSEQ"は非常に時間がかかる(数時間というレベル)ので覚悟しておいたほうがいいです。 Gene symbol ("SYMBOL") やEntrez ID ("ENTREZID")は比較的利用頻度が高いのでそれぞれ独立した項目として示しています。
param1 <- "rat2302.db" #パッケージ名を指定 #必要なパッケージをロード library(param1, character.only=T) #param1で指定したパッケージの読み込み #本番(利用可能なアノテーション情報を表示) keytypes(eval(parse(text=param1))) #利用可能なアノテーション情報を表示
代表値(要約統計量)は、平均値(mean)、中央値(median)、最大値(max)など好きなものを指定できます。 この作業はGSEA解析でも当然やります。"Collapse dataset to gene symbols"に相当するところです。 GSEAでは「最大値(このページ中での関数はmaxでGSEAの"max_probe (default)"に相当)」または 「中央値(このページ中での関数はmedianでGSEAの"median_of_probes"に相当)」が選択可能です。
GAGEパッケージ(Luo et al., 2009) のProbe set ID conversionの項目で書いているものと同じことをやっているだけ、という理解で差支えありません。
前処理 | ID変換 | probe ID --> gene symbol
probe IDの遺伝子発現行列を入力として、gene symbolの遺伝子発現行列を出力するやり方を示します。 probe IDとgene symbolの対応関係情報が必要ですので、様々なやり方を示しています。 同じgene symbolをもつ複数のprobe IDsが存在する場合にはparamで指定した方法で要約統計量を計算します。 代表値(要約統計量)は、平均値(mean)、中央値(median)、 最大値(max)など好きなものを指定できます。 「hoge3_GPL1355.txtの1列目のID情報の対応がとれる(同じ行の位置でなくてもよい)」と書いていましたが、 実際には同じ行の位置にしておかねばならなかったことが判明しました。大変失礼しましたm(_ _)m。 2017年9月22に修正しましたので、例題2以降は言葉通りになっているはずです(2017.09.22追加)。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し、以下をコピペ
1. サンプルデータ20の31,099 probesets×24 samplesのRMA-preprocessedデータ(data_rma_2.txt)の場合:
Affymetrix Rat Genome 230 2.0 Arrayを用いて得られたNakai et al., BBB, 2008のデータです。 イントロ | アノテーション情報取得 | GEOquery(Davis_2007)の3を行って得られたhoge3_GPL1355.txtの情報も利用しています。 data_rma_2.txtの1列目のID情報とhoge3_GPL1355.txtの1列目のID情報の対応がとれる(同じ行の位置でなければならない)ことが前提です。 1分程度で終わります。
in_f1 <- "data_rma_2.txt" #入力ファイル名を指定してin_f1に格納(発現データ) in_f2 <- "hoge3_GPL1355.txt" #入力ファイル名を指定してin_f2に格納(Gene symbolとIDの対応表のデータ) out_f <- "hoge1.txt" #出力ファイル名を指定してout_fに格納 param <- mean #代表値を指定 #前処理(IDとGene symbolとの対応関係を含む情報を入手) sym <- read.table(in_f2, header=TRUE, row.names=1, sep="\t", quote="")#in_f2で指定したファイルの読み込み IDs <- as.vector(sym[,1]) #Gene symbol情報をベクトルに変換し、IDsに格納 names(IDs) <- rownames(sym) #IDsを行名で対応づけられるようにしている uniqID <- unique(IDs) #non-redundant ID情報を抽出し、uniqIDに格納 uniqID <- uniqID[uniqID != ""] #uniqIDの中から指定したIDがないものを除く uniqID <- uniqID[!is.na(uniqID)] #uniqIDの中から指定したIDが"NA"のものを除く uniqID <- uniqID[!is.nan(uniqID)] #uniqIDの中から指定したIDが"NaN"のものを除く #本番 data <- read.table(in_f1, header=TRUE, row.names=1, sep="\t", quote="")#in_f1で指定したファイルの読み込み hoge <- t(apply(as.matrix(uniqID), 1, function(i, d = data, s = IDs, p = param) {#uniqIDを一つずつ処理する apply(d[which(s == i), ], 2, p, na.rm = TRUE)#dataの中から現在のgene symbol(i)と同じprobesを全て抽出し、その平均値(mean)を返す }, data, IDs, param)) #apply関数でdata,IDs,paramを使えるように代入 rownames(hoge) <- uniqID #non-redundant IDをhogeの行の名前として利用 #ファイルに保存 tmp <- cbind(rownames(hoge), hoge) #指定したIDの列を行列hogeの左端に挿入し、結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
2. サンプルデータ20の31,099 probesets×24 samplesのRMA-preprocessedデータ(data_rma_2.txt)の場合:
Affymetrix Rat Genome 230 2.0 Arrayを用いて得られたNakai et al., BBB, 2008のデータです。 イントロ | アノテーション情報取得 | GEOquery(Davis_2007)の3を行って得られたhoge3_GPL1355.txtの情報も利用しています。 data_rma_2.txtの1列目のID情報とhoge3_GPL1355.txtの1列目のID情報の対応がとれる(同じ行の位置でなくてもよい)ことが前提です。 2分程度で終わります。
in_f1 <- "data_rma_2.txt" #入力ファイル名を指定してin_f1に格納(発現データ) in_f2 <- "hoge3_GPL1355.txt" #入力ファイル名を指定してin_f2に格納(Gene symbolとIDの対応表のデータ) out_f <- "hoge2.txt" #出力ファイル名を指定してout_fに格納 param <- mean #代表値を指定 #前処理(IDとGene symbolとの対応関係を含む情報を入手) sym <- read.table(in_f2, header=TRUE, row.names=1, sep="\t", quote="")#in_f2で指定したファイルの読み込み IDs <- as.vector(sym[,1]) #Gene symbol情報をベクトルに変換し、IDsに格納 names(IDs) <- rownames(sym) #IDsを行名で対応づけられるようにしている uniqID <- unique(IDs) #non-redundant ID情報を抽出し、uniqIDに格納 uniqID <- uniqID[uniqID != ""] #uniqIDの中から指定したIDがないものを除く uniqID <- uniqID[!is.na(uniqID)] #uniqIDの中から指定したIDが"NA"のものを除く uniqID <- uniqID[!is.nan(uniqID)] #uniqIDの中から指定したIDが"NaN"のものを除く #本番 data <- read.table(in_f1, header=TRUE, row.names=1, sep="\t", quote="")#in_f1で指定したファイルの読み込み hoge <- NULL #最終的に欲しい情報を格納するためのプレースホルダ for(i in 1:length(uniqID)){ #non-redundant ID数分だけループを回す obj <- is.element(IDs, uniqID[i]) #条件を満たすかどうかを判定した結果をobjに格納(IDsベクトル内でi番目のuniqIDと一致する位置をTRUE) hoge <- rbind(hoge, apply(data[names(IDs[obj]),], 2, param, na.rm=TRUE))#dataの中からi番目の指定したIDと同じprobesを全て抽出し、そのparamで指定した代表値をhogeの一番下の行に追加 #hoge <- rbind(hoge, apply(data[which(IDs == uniqID[i]),], 2, param, na.rm=TRUE))#dataの中からi番目の指定したIDと同じprobesを全て抽出し、そのparamで指定した代表値をhogeの一番下の行に追加 } #non-redundant ID数分だけループを回す rownames(hoge) <- uniqID #non-redundant IDをhogeの行の名前として利用 #ファイルに保存 tmp <- cbind(rownames(hoge), hoge) #指定したIDの列を行列hogeの左端に挿入し、結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
3. サンプルデータ13のsample13_7vs7.txt)の場合:
Agilent-012097 Human 1A Microarray (V2) G4110B (Feature Number version)を用いて得られたデータです。 イントロ | アノテーション情報取得 | GEOquery(Davis_2007)の6を行って得られたhoge6_GPL887.txtの情報も利用しています。 sample13_7vs7.txtの1列目のID情報とhoge6_GPL887.txtの1列目のID情報の対応がとれる(同じ行の位置でなくてもよい)ことが前提です。 2分程度で終わります。以下は、入力ファイル中の7810と9681というIDが同じGene symbol(ABCA10)にまとめられる(collapsing)イメージです。(NA --> NaNになっているところは本質的な部分ではありません...。)
入力:

出力:

in_f1 <- "sample13_7vs7.txt" #入力ファイル名を指定してin_f1に格納(発現データ) in_f2 <- "hoge6_GPL887.txt" #入力ファイル名を指定してin_f2に格納(Gene symbolとIDの対応表のデータ) out_f <- "hoge3.txt" #出力ファイル名を指定してout_fに格納 param <- mean #代表値を指定 #前処理(IDとGene symbolとの対応関係を含む情報を入手) sym <- read.table(in_f2, header=TRUE, row.names=1, sep="\t", quote="")#in_f2で指定したファイルの読み込み IDs <- as.vector(sym[,1]) #Gene symbol情報をベクトルに変換し、IDsに格納 names(IDs) <- rownames(sym) #IDsを行名で対応づけられるようにしている uniqID <- unique(IDs) #non-redundant ID情報を抽出し、uniqIDに格納 uniqID <- uniqID[uniqID != ""] #uniqIDの中から指定したIDがないものを除く uniqID <- uniqID[!is.na(uniqID)] #uniqIDの中から指定したIDが"NA"のものを除く uniqID <- uniqID[!is.nan(uniqID)] #uniqIDの中から指定したIDが"NaN"のものを除く #本番 data <- read.table(in_f1, header=TRUE, row.names=1, sep="\t", quote="")#in_f1で指定したファイルの読み込み hoge <- NULL #最終的に欲しい情報を格納するためのプレースホルダ for(i in 1:length(uniqID)){ #non-redundant ID数分だけループを回す obj <- is.element(IDs, uniqID[i]) #条件を満たすかどうかを判定した結果をobjに格納(IDsベクトル内でi番目のuniqIDと一致する位置をTRUE) hoge <- rbind(hoge, apply(data[names(IDs[obj]),], 2, param, na.rm=TRUE))#dataの中からi番目の指定したIDと同じprobesを全て抽出し、そのparamで指定した代表値をhogeの一番下の行に追加 #hoge <- rbind(hoge, apply(data[which(IDs == uniqID[i]),], 2, param, na.rm=TRUE))#dataの中からi番目の指定したIDと同じprobesを全て抽出し、そのparamで指定した代表値をhogeの一番下の行に追加 } #non-redundant ID数分だけループを回す rownames(hoge) <- uniqID #non-redundant IDをhogeの行の名前として利用 #ファイルに保存 tmp <- cbind(rownames(hoge), hoge) #指定したIDの列を行列hogeの左端に挿入し、結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
4. サンプルデータ20の31,099 probesets×24 samplesのRMA-preprocessedデータ(data_rma_2.txt)の場合:
Affymetrix Rat Genome 230 2.0 Arrayを用いて得られたNakai et al., BBB, 2008のデータです。 イントロ | アノテーション情報取得 | Rのパッケージ*.dbからを参考にして得られたprobe IDとGene symbolとの対応関係を含む情報を利用するやり方です。 パッケージのダウンロードで時間がかかるかもしれません。1や2の結果と出力ファイルの行数や数値が若干違うのは、おそらくアノテーションのバージョンの違いによるものだろうと思っています。
in_f <- "data_rma_2.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge4.txt" #出力ファイル名を指定してout_fに格納 param <- mean #代表値を指定 param1 <- "rat2302.db" #パッケージ名を指定 param2 <- "SYMBOL" #欲しいアノテーション情報を指定(記述可能なリストは以下のkeytypes(dbname)から取得可能) #必要なパッケージのインストール(必要に応じて#を外して実行すべし) #source("http://bioconductor.org/biocLite.R")#指定したパッケージのインストール #biocLite(param1, suppressUpdates=TRUE)#指定したパッケージのインストール #必要なパッケージをロード library(param1, character.only=T) #param1で指定したパッケージの読み込み #probe IDと指定したIDとの対応関係を含む情報を入手 hoge <- sub(".db", param2, param1) #用いたいオブジェクト名情報を取得(hgu133aSYMBOLに相当) hoge <- eval(parse(text=hoge)) #hogeを文字列としてではなくオブジェクトとして取り扱う IDs <- unlist(as.list(hoge)) #全probesに対応する指定したID情報を抽出し、IDsに格納 uniqID <- unique(IDs) #non-redundant ID情報を抽出し、uniqIDに格納 uniqID <- uniqID[uniqID != ""] #uniqIDの中から指定したIDがないものを除く uniqID <- uniqID[!is.na(uniqID)] #uniqIDの中から指定したIDが"NA"のものを除く uniqID <- uniqID[!is.nan(uniqID)] #uniqIDの中から指定したIDが"NaN"のものを除く #本番 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み hoge <- NULL #最終的に欲しい情報を格納するためのプレースホルダ for(i in 1:length(uniqID)){ #non-redundant ID数分だけループを回す obj <- is.element(IDs, uniqID[i]) #条件を満たすかどうかを判定した結果をobjに格納(IDsベクトル内でi番目のuniqIDと一致する位置をTRUE) hoge <- rbind(hoge, apply(data[names(IDs[obj]),], 2, param, na.rm=TRUE))#dataの中からi番目の指定したIDと同じprobesを全て抽出し、そのparamで指定した代表値をhogeの一番下の行に追加 #hoge <- rbind(hoge, apply(data[which(IDs == uniqID[i]),], 2, param, na.rm=TRUE))#dataの中からi番目の指定したIDと同じprobesを全て抽出し、そのparamで指定した代表値をhogeの一番下の行に追加 } #non-redundant ID数分だけループを回す rownames(hoge) <- uniqID #non-redundant IDをhogeの行の名前として利用 #ファイルに保存 tmp <- cbind(rownames(hoge), hoge) #指定したIDの列を行列hogeの左端に挿入し、結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
5. サンプルデータ5の22,283 probesets×36 samplesのRMA-preprocessedデータ(sample5.txt)の場合:
Affymetrix Human Genome U133A Array (GPL96)を用いて得られたGe et al., Genomics, 2005のデータです。 イントロ | アノテーション情報取得 | Rのパッケージ*.dbからを参考にして得られたprobe IDとGene symbolとの対応関係を含む情報を利用するやり方です。
in_f <- "sample5.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge5.txt" #出力ファイル名を指定してout_fに格納 param <- mean #代表値を指定 param1 <- "hgu133a.db" #パッケージ名を指定 param2 <- "SYMBOL" #欲しいアノテーション情報を指定(記述可能なリストは以下のkeytypes(dbname)から取得可能) #必要なパッケージのインストール(必要に応じて#を外して実行すべし) #source("http://bioconductor.org/biocLite.R")#指定したパッケージのインストール #biocLite(param1, suppressUpdates=TRUE)#指定したパッケージのインストール #必要なパッケージをロード library(param1, character.only=T) #param1で指定したパッケージの読み込み #probe IDと指定したIDとの対応関係を含む情報を入手 hoge <- sub(".db", param2, param1) #用いたいオブジェクト名情報を取得(hgu133aSYMBOLに相当) hoge <- eval(parse(text=hoge)) #hogeを文字列としてではなくオブジェクトとして取り扱う IDs <- unlist(as.list(hoge)) #全probesに対応する指定したID情報を抽出し、IDsに格納 uniqID <- unique(IDs) #non-redundant ID情報を抽出し、uniqIDに格納 uniqID <- uniqID[uniqID != ""] #uniqIDの中から指定したIDがないものを除く uniqID <- uniqID[!is.na(uniqID)] #uniqIDの中から指定したIDが"NA"のものを除く uniqID <- uniqID[!is.nan(uniqID)] #uniqIDの中から指定したIDが"NaN"のものを除く #本番 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み hoge <- NULL #最終的に欲しい情報を格納するためのプレースホルダ for(i in 1:length(uniqID)){ #non-redundant ID数分だけループを回す obj <- is.element(IDs, uniqID[i]) #条件を満たすかどうかを判定した結果をobjに格納(IDsベクトル内でi番目のuniqIDと一致する位置をTRUE) hoge <- rbind(hoge, apply(data[names(IDs[obj]),], 2, param, na.rm=TRUE))#dataの中からi番目の指定したIDと同じprobesを全て抽出し、そのparamで指定した代表値をhogeの一番下の行に追加 #hoge <- rbind(hoge, apply(data[which(IDs == uniqID[i]),], 2, param, na.rm=TRUE))#dataの中からi番目の指定したIDと同じprobesを全て抽出し、そのparamで指定した代表値をhogeの一番下の行に追加 } #non-redundant ID数分だけループを回す rownames(hoge) <- uniqID #non-redundant IDをhogeの行の名前として利用 #ファイルに保存 tmp <- cbind(rownames(hoge), hoge) #指定したIDの列を行列hogeの左端に挿入し、結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
前処理 | ID変換 | probe ID --> Entrez ID
probe IDの遺伝子発現行列を入力として、Entrez IDの遺伝子発現行列を出力するやり方を示します。 probe IDとEntrez IDの対応関係情報が必要ですので、様々なやり方を示しています。 同じEntrez IDをもつ複数のprobe IDsが存在する場合にはparamで指定した方法で要約統計量を計算します。 代表値(要約統計量)は、平均値(mean)、中央値(median)、 最大値(max)など好きなものを指定できます。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し、以下をコピペ
1. サンプルデータ20の31,099 probesets×24 samplesのRMA-preprocessedデータ(data_rma_2.txt)の場合:
Affymetrix Rat Genome 230 2.0 Arrayを用いて得られたNakai et al., BBB, 2008のデータです。
イントロ | アノテーション情報取得 | Rのパッケージ*.dbからを参考にして得られたprobe IDとEntrez IDとの対応関係を含む情報を利用するやり方です。
in_f <- "data_rma_2.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge1.txt" #出力ファイル名を指定してout_fに格納 param <- mean #代表値を指定 param1 <- "rat2302.db" #パッケージ名を指定 param2 <- "ENTREZID" #欲しいアノテーション情報を指定(記述可能なリストは以下のkeytypes(dbname)から取得可能) #必要なパッケージのインストール(必要に応じて#を外して実行すべし) #source("http://bioconductor.org/biocLite.R")#指定したパッケージのインストール #biocLite(param1, suppressUpdates=TRUE)#指定したパッケージのインストール #必要なパッケージをロード library(param1, character.only=T) #param1で指定したパッケージの読み込み #probe IDと指定したIDとの対応関係を含む情報を入手 hoge <- sub(".db", param2, param1) #用いたいオブジェクト名情報を取得(rat2302ENTREZIDに相当) hoge <- eval(parse(text=hoge)) #hogeを文字列としてではなくオブジェクトとして取り扱う IDs <- unlist(as.list(hoge)) #全probesに対応する指定したID情報を抽出し、IDsに格納 uniqID <- unique(IDs) #non-redundant ID情報を抽出し、uniqIDに格納 uniqID <- uniqID[uniqID != ""] #uniqIDの中から指定したIDがないものを除く uniqID <- uniqID[!is.na(uniqID)] #uniqIDの中から指定したIDが"NA"のものを除く uniqID <- uniqID[!is.nan(uniqID)] #uniqIDの中から指定したIDが"NaN"のものを除く #本番 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み hoge <- NULL #最終的に欲しい情報を格納するためのプレースホルダ for(i in 1:length(uniqID)){ #non-redundant ID数分だけループを回す hoge <- rbind(hoge, apply(data[which(IDs == uniqID[i]),], 2, param, na.rm=TRUE))#dataの中からi番目の指定したIDと同じprobesを全て抽出し、そのparamで指定した代表値をhogeの一番下の行に追加 } #non-redundant ID数分だけループを回す rownames(hoge) <- uniqID #non-redundant IDをhogeの行の名前として利用 #ファイルに保存 tmp <- cbind(rownames(hoge), hoge) #指定したIDの列を行列hogeの左端に挿入し、結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
2. サンプルデータ5の22,283 probesets×36 samplesのRMA-preprocessedデータ(sample5.txt)の場合:
Affymetrix Human Genome U133A Array (GPL96)を用いて得られたGe et al., Genomics, 2005のデータです。
イントロ | アノテーション情報取得 | Rのパッケージ*.dbからを参考にして得られたprobe IDとEntrez IDとの対応関係を含む情報を利用するやり方です。
in_f <- "sample5.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge2.txt" #出力ファイル名を指定してout_fに格納 param <- mean #代表値を指定 param1 <- "hgu133a.db" #パッケージ名を指定 param2 <- "ENTREZID" #欲しいアノテーション情報を指定(記述可能なリストは以下のkeytypes(dbname)から取得可能) #必要なパッケージのインストール(必要に応じて#を外して実行すべし) #source("http://bioconductor.org/biocLite.R")#指定したパッケージのインストール #biocLite(param1, suppressUpdates=TRUE)#指定したパッケージのインストール #必要なパッケージをロード library(param1, character.only=T) #param1で指定したパッケージの読み込み #probe IDと指定したIDとの対応関係を含む情報を入手 hoge <- sub(".db", param2, param1) #用いたいオブジェクト名情報を取得hgu133aENTREZIDに相当) hoge <- eval(parse(text=hoge)) #hogeを文字列としてではなくオブジェクトとして取り扱う IDs <- unlist(as.list(hoge)) #全probesに対応する指定したID情報を抽出し、IDsに格納 uniqID <- unique(IDs) #non-redundant ID情報を抽出し、uniqIDに格納 uniqID <- uniqID[uniqID != ""] #uniqIDの中から指定したIDがないものを除く uniqID <- uniqID[!is.na(uniqID)] #uniqIDの中から指定したIDが"NA"のものを除く uniqID <- uniqID[!is.nan(uniqID)] #uniqIDの中から指定したIDが"NaN"のものを除く #本番 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み hoge <- NULL #最終的に欲しい情報を格納するためのプレースホルダ for(i in 1:length(uniqID)){ #non-redundant ID数分だけループを回す hoge <- rbind(hoge, apply(data[which(IDs == uniqID[i]),], 2, param, na.rm=TRUE))#dataの中からi番目の指定したIDと同じprobesを全て抽出し、そのparamで指定した代表値をhogeの一番下の行に追加 } #non-redundant ID数分だけループを回す rownames(hoge) <- uniqID #non-redundant IDをhogeの行の名前として利用 #ファイルに保存 tmp <- cbind(rownames(hoge), hoge) #指定したIDの列を行列hogeの左端に挿入し、結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
前処理 | ID変換 | probe ID --> その他
probe IDの遺伝子発現行列を入力として、(gene symbolとEntrez ID以外の)ENSEMBLやUNIGENEの遺伝子発現行列を出力するやり方を示します。 probe IDと指定したIDの対応関係情報が必要ですので、様々なやり方を示しています。 同じIDをもつ複数のprobe IDsが存在する場合にはparamで指定した方法で要約統計量を計算します。 代表値(要約統計量)は、平均値(mean)、中央値(median)、 最大値(max)など好きなものを指定できます。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し、以下をコピペ
probeset IDから下記で示すようなIDに変換することができます: "ACCNUM", "REFSEQ", "UNIGENE", "ENSEMBL", "ENSEMBLPROT", "ENSEMBLTRANS", "GENENAME", "PFAM", "PROSITE"。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し、以下をコピペ
1. サンプルデータ20の31,099 probesets×24 samplesのRMA-preprocessedデータ(data_rma_2.txt)の場合:
Affymetrix Rat Genome 230 2.0 Arrayを用いて得られたNakai et al., BBB, 2008のデータです。
イントロ | アノテーション情報取得 | Rのパッケージ*.dbからを参考にして得られたprobe IDとENSEMBL IDとの対応関係を含む情報を利用するやり方です。
in_f <- "data_rma_2.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge1.txt" #出力ファイル名を指定してout_fに格納 param <- mean #代表値を指定 param1 <- "rat2302.db" #パッケージ名を指定 param2 <- "ENSEMBL" #欲しいアノテーション情報を指定(記述可能なリストは以下のkeytypes(dbname)から取得可能) #必要なパッケージのインストール(必要に応じて#を外して実行すべし) #source("http://bioconductor.org/biocLite.R")#指定したパッケージのインストール #biocLite(param1, suppressUpdates=TRUE)#指定したパッケージのインストール #必要なパッケージをロード library(param1, character.only=T) #param1で指定したパッケージの読み込み #probe IDと指定したIDとの対応関係を含む情報を入手 hoge <- sub(".db", param2, param1) #用いたいオブジェクト名情報を取得(rat2302ENSEMBLに相当) hoge <- eval(parse(text=hoge)) #hogeを文字列としてではなくオブジェクトとして取り扱う IDs <- unlist(as.list(hoge)) #全probesに対応する指定したID情報を抽出し、IDsに格納 uniqID <- unique(IDs) #non-redundant ID情報を抽出し、uniqIDに格納 uniqID <- uniqID[uniqID != ""] #uniqIDの中から指定したIDがないものを除く uniqID <- uniqID[!is.na(uniqID)] #uniqIDの中から指定したIDが"NA"のものを除く uniqID <- uniqID[!is.nan(uniqID)] #uniqIDの中から指定したIDが"NaN"のものを除く #本番 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み hoge <- NULL #最終的に欲しい情報を格納するためのプレースホルダ for(i in 1:length(uniqID)){ #non-redundant ID数分だけループを回す hoge <- rbind(hoge, apply(data[which(IDs == uniqID[i]),], 2, param, na.rm=TRUE))#dataの中からi番目の指定したIDと同じprobesを全て抽出し、そのparamで指定した代表値をhogeの一番下の行に追加 } #non-redundant ID数分だけループを回す rownames(hoge) <- uniqID #non-redundant IDをhogeの行の名前として利用 #ファイルに保存 tmp <- cbind(rownames(hoge), hoge) #指定したIDの列を行列hogeの左端に挿入し、結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
2. サンプルデータ5の22,283 probesets×36 samplesのRMA-preprocessedデータ(sample5.txt)の場合:
Affymetrix Human Genome U133A Array (GPL96)を用いて得られたGe et al., Genomics, 2005のデータです。
イントロ | アノテーション情報取得 | Rのパッケージ*.dbからを参考にして得られたprobe IDとUNIGENE IDとの対応関係を含む情報を利用するやり方です。
in_f <- "sample5.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge2.txt" #出力ファイル名を指定してout_fに格納 param <- mean #代表値を指定 param1 <- "hgu133a.db" #パッケージ名を指定 param2 <- "UNIGENE" #欲しいアノテーション情報を指定(記述可能なリストは以下のkeytypes(dbname)から取得可能) #必要なパッケージのインストール(必要に応じて#を外して実行すべし) #source("http://bioconductor.org/biocLite.R")#指定したパッケージのインストール #biocLite(param1, suppressUpdates=TRUE)#指定したパッケージのインストール #必要なパッケージをロード library(param1, character.only=T) #param1で指定したパッケージの読み込み #probe IDと指定したIDとの対応関係を含む情報を入手 hoge <- sub(".db", param2, param1) #用いたいオブジェクト名情報を取得(hgu133aUNIGENEに相当) hoge <- eval(parse(text=hoge)) #hogeを文字列としてではなくオブジェクトとして取り扱う IDs <- unlist(as.list(hoge)) #全probesに対応する指定したID情報を抽出し、IDsに格納 uniqID <- unique(IDs) #non-redundant ID情報を抽出し、uniqIDに格納 uniqID <- uniqID[uniqID != ""] #uniqIDの中から指定したIDがないものを除く uniqID <- uniqID[!is.na(uniqID)] #uniqIDの中から指定したIDが"NA"のものを除く uniqID <- uniqID[!is.nan(uniqID)] #uniqIDの中から指定したIDが"NaN"のものを除く #本番 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み hoge <- NULL #最終的に欲しい情報を格納するためのプレースホルダ for(i in 1:length(uniqID)){ #non-redundant ID数分だけループを回す hoge <- rbind(hoge, apply(data[which(IDs == uniqID[i]),], 2, param, na.rm=TRUE))#dataの中からi番目の指定したIDと同じprobesを全て抽出し、そのparamで指定した代表値をhogeの一番下の行に追加 } #non-redundant ID数分だけループを回す rownames(hoge) <- uniqID #non-redundant IDをhogeの行の名前として利用 #ファイルに保存 tmp <- cbind(rownames(hoge), hoge) #指定したIDの列を行列hogeの左端に挿入し、結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
前処理 | ID変換 | 同じ遺伝子名を持つものをまとめる
例えば、「酸化的リン酸化」のパスウェイに関連する遺伝子セットが自分が見ている条件間で全体として動いているかどうかを調べたい場合に、 解析 | 機能解析 | 遺伝子オントロジー(GO)解析 | についてや解析 | 機能解析 | パスウェイ(Pathway)解析 | について で述べている方法を利用しますが、これを実行するための入力ファイルをここで作成する必要があります。 そのため、「酸化的リン酸化」のパスウェイに関連する遺伝子セット中の特定の遺伝子(遺伝子A)が自分が見ている条件間で発現変動していて、 しかもチップ上に重複して多数(別のプローブIDとして)搭載されているような場合には、遺伝子Aだけの効果でそのパスウェイが「動いている」などという誤った結果を導きかねません。 このようなチップ上の重複遺伝子の効果を排除すべく、同じ遺伝子名をもつ複数のプローブIDの発現プロファイルに対しては、 その代表値(平均値(mean)や中央値(median)など)を出力して、 遺伝子名の重複のない(non-redundant)遺伝子発現行列をファイルとして得たいときに以下の作業を行います。
non-redundantにするためには、プローブIDとgene symbolやEntrez Gene IDとの対応表が必要になります。 この情報はイントロ | アノテーション情報取得 | 公共DB(GEO)からの6までを行うことで、 GPL1355-14795_symbol.txtのような形式の対応表ファイルとして入力時に読み込ませる戦略や、 Pathviewパッケージ(Luo et al., 2013)中のID変換用関数などを利用する戦略があります。 代表値(要約統計量)は、平均値(mean)、中央値(median)、最大値(max)など好きなものを指定できます。 この作業はGSEA解析でも当然やります。"Collapse dataset to gene symbols"に相当するところです。 GSEAでは「最大値(このページ中での関数はmaxでGSEAの"max_probe (default)"に相当)」または 「中央値(このページ中での関数はmedianでGSEAの"median_of_probes"に相当)」が選択可能です。
例題の多くは、probeset IDからgene symbolへの変換ですが、Entrez IDへの変換なども同じ枠組みでできます。 ここでやっているのは異なるIDの変換(ID converter)です。GAGEパッケージ(Luo et al., 2009) のProbe set ID conversionの項目で書いているものと同じことをやっているだけ、という理解で差支えありません。
1. サンプルデータ20の31,099 probesets×24 samplesのRMA-preprocessedデータ(data_rma_2.txt)の場合:
Affymetrix Rat Genome 230 2.0 Arrayを用いて得られたNakai et al., BBB, 2008のデータです。
イントロ | アノテーション情報取得 | 公共DB(GEO)からの6までを行って得たGPL1355-14795_symbol.txtの情報も利用しています。
data_rma_2.txtの1列目のID情報とGPL1355-14795_symbol.txtの1列目のID情報の対応がとれる(同じ行の位置でなくてもよい)ことが前提です。 1分程度で終わります。
data_rma_2_nr.txtはこのコードを実行して得られたものです。
in_f1 <- "data_rma_2.txt" #入力ファイル名を指定してin_f1に格納(発現データ) in_f2 <- "GPL1355-14795_symbol.txt" #入力ファイル名を指定してin_f2に格納(Gene symbolとIDの対応表のデータ) out_f <- "hoge1.txt" #出力ファイル名を指定してout_fに格納 param <- mean #代表値を指定 #前処理(IDとGene symbolとの対応関係を含む情報を入手) sym <- read.table(in_f2, header=TRUE, row.names=1, sep="\t", quote="")#in_f2で指定したファイルの読み込み symbols <- as.vector(sym[,1]) #Gene symbol情報をベクトルに変換し、symbolsに格納 names(symbols) <- rownames(sym) #symbolsをIDで対応づけられるようにしている unique_sym <- unique(symbols) #symbolsの中からnon-redundantな情報のみを抽出し、unique_symに格納 unique_sym <- unique_sym[unique_sym != ""]#unique_symの中から、Gene symbolがないものを除く unique_sym <- unique_sym[!is.na(unique_sym)]#unique_symの中から、Gene symbolが"NA"のものを除く unique_sym <- unique_sym[!is.nan(unique_sym)]#unique_symの中から、Gene symbolが"NaN"のものを除く #本番 data <- read.table(in_f1, header=TRUE, row.names=1, sep="\t", quote="")#in_f1で指定したファイルの読み込み hoge <- t(apply(as.matrix(unique_sym), 1, function(i, d = data, s = symbols, p = param) {#unique_symを一つずつ処理する apply(d[which(s == i), ], 2, p, na.rm = TRUE)#dataの中から現在のgene symbol(i)と同じprobesを全て抽出し、その平均値(mean)を返す }, data, symbols, param)) #apply関数でdata,symbols,paramを使えるように代入 rownames(hoge) <- unique_sym #non-redundant gene symbolsをhogeの行の名前として利用 #ファイルに保存 tmp <- cbind(rownames(hoge), hoge) #遺伝子IDの列を行列hogeの左端に挿入し、結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
2. サンプルデータ20の31,099 probesets×24 samplesのRMA-preprocessedデータ(data_rma_2.txt)の場合:
Affymetrix Rat Genome 230 2.0 Arrayを用いて得られたNakai et al., BBB, 2008のデータです。
イントロ | アノテーション情報取得 | 公共DB(GEO)からの6までを行って得たGPL1355-14795_symbol.txtの情報も利用しています。
data_rma_2.txtの1列目のID情報とGPL1355-14795_symbol.txtの1列目のID情報の対応がとれる(同じ行の位置でなくてもよい)ことが前提です。 2分程度で終わります。
data_rma_2_nr.txtはこのコードを実行して得られたものです。
in_f1 <- "data_rma_2.txt" #入力ファイル名を指定してin_f1に格納(発現データ) in_f2 <- "GPL1355-14795_symbol.txt" #入力ファイル名を指定してin_f2に格納(Gene symbolとIDの対応表のデータ) out_f <- "hoge2.txt" #出力ファイル名を指定してout_fに格納 param <- mean #代表値を指定 #前処理(IDとGene symbolとの対応関係を含む情報を入手) sym <- read.table(in_f2, header=TRUE, row.names=1, sep="\t", quote="")#in_f2で指定したファイルの読み込み symbols <- as.vector(sym[,1]) #Gene symbol情報をベクトルに変換し、symbolsに格納 names(symbols) <- rownames(sym) #symbolsをIDで対応づけられるようにしている unique_sym <- unique(symbols) #symbolsの中からnon-redundantな情報のみを抽出し、unique_symに格納 unique_sym <- unique_sym[unique_sym != ""]#unique_symの中から、Gene symbolがないものを除く unique_sym <- unique_sym[!is.na(unique_sym)]#unique_symの中から、Gene symbolが"NA"のものを除く unique_sym <- unique_sym[!is.nan(unique_sym)]#unique_symの中から、Gene symbolが"NaN"のものを除く #本番 data <- read.table(in_f1, header=TRUE, row.names=1, sep="\t", quote="")#in_f1で指定したファイルの読み込み hoge <- NULL #最終的に欲しい情報を格納するためのプレースホルダ for(i in 1:length(unique_sym)){ #non-redundant gene symbol数分だけループを回す hoge <- rbind(hoge, apply(data[which(symbols == unique_sym[i]),], 2, param, na.rm=TRUE))#dataの中からi番目のgene symbolと同じprobesを全て抽出し、その平均値(mean)をhogeの一番下の行に追加 } #non-redundant gene symbol数分だけループを回す rownames(hoge) <- unique_sym #non-redundant gene symbolsをhogeの行の名前として利用 #ファイルに保存 tmp <- cbind(rownames(hoge), hoge) #遺伝子IDの列を行列hogeの左端に挿入し、結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
3. サンプルデータ13のsample13_7vs7.txt)の場合:
Agilent-012097 Human 1A Microarray (V2) G4110B (Feature Number version)を用いて得られたデータです。
イントロ | アノテーション情報取得 | 公共DB(GEO)からの6までを行って得たGPL887-5640_symbol.txtの情報も利用しています。
sample13_7vs7.txtの1列目のID情報とGPL887-5640_symbol.txtの1列目のID情報の対応がとれる(同じ行の位置でなくてもよい)ことが前提です。 2分程度で終わります。以下は、入力ファイル中の7810と9681というIDが同じGene symbol(ABCA10)にまとめられる(collapsing)イメージです。(NA --> NaNになっているところは本質的な部分ではありません...。)
入力:

出力:

in_f1 <- "sample13_7vs7.txt" #入力ファイル名を指定してin_f1に格納(発現データ) in_f2 <- "GPL887-5640_symbol.txt" #入力ファイル名を指定してin_f2に格納(Gene symbolとIDの対応表のデータ) out_f <- "hoge3.txt" #出力ファイル名を指定してout_fに格納 param <- mean #代表値を指定 #前処理(IDとGene symbolとの対応関係を含む情報を入手) sym <- read.table(in_f2, header=TRUE, row.names=1, sep="\t", quote="")#in_f2で指定したファイルの読み込み symbols <- as.vector(sym[,1]) #Gene symbol情報をベクトルに変換し、symbolsに格納 names(symbols) <- rownames(sym) #symbolsをIDで対応づけられるようにしている unique_sym <- unique(symbols) #symbolsの中からnon-redundantな情報のみを抽出し、unique_symに格納 unique_sym <- unique_sym[unique_sym != ""]#unique_symの中から、Gene symbolがないものを除く unique_sym <- unique_sym[!is.na(unique_sym)]#unique_symの中から、Gene symbolが"NA"のものを除く unique_sym <- unique_sym[!is.nan(unique_sym)]#unique_symの中から、Gene symbolが"NaN"のものを除く #本番 data <- read.table(in_f1, header=TRUE, row.names=1, sep="\t", quote="")#in_f1で指定したファイルの読み込み hoge <- NULL #最終的に欲しい情報を格納するためのプレースホルダ for(i in 1:length(unique_sym)){ #non-redundant gene symbol数分だけループを回す hoge <- rbind(hoge, apply(data[which(symbols == unique_sym[i]),], 2, param, na.rm=TRUE))#dataの中からi番目のgene symbolと同じprobesを全て抽出し、その平均値(mean)をhogeの一番下の行に追加 } #non-redundant gene symbol数分だけループを回す rownames(hoge) <- unique_sym #non-redundant gene symbolsをhogeの行の名前として利用 #ファイルに保存 tmp <- cbind(rownames(hoge), hoge) #遺伝子IDの列を行列hogeの左端に挿入し、結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
4. サンプルデータ20の31,099 probesets×24 samplesのRMA-preprocessedデータ(data_rma_2.txt)の場合:
Affymetrix Rat Genome 230 2.0 Arrayを用いて得られたNakai et al., BBB, 2008のデータです。
イントロ | アノテーション情報取得 | Rのパッケージ*.dbからを参考にして得られたprobe IDとGene symbolとの対応関係を含む情報を利用するやり方です。 パッケージのダウンロードで時間がかかるかもしれません。1や2の結果と出力ファイルの行数や数値が若干違うのは、おそらくアノテーションのバージョンの違いによるものだろうと思っています。
in_f <- "data_rma_2.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge4.txt" #出力ファイル名を指定してout_fに格納 param <- mean #代表値を指定 param1 <- "rat2302.db" #パッケージ名を指定 param2 <- "SYMBOL" #欲しいアノテーション情報を指定(記述可能なリストは以下のkeytypes(dbname)から取得可能) #必要なパッケージのインストール(利用したいパッケージが既に存在していれば2回目以降は必要なし) source("http://bioconductor.org/biocLite.R")#指定したパッケージのインストール biocLite(param1, suppressUpdates=TRUE) #指定したパッケージのインストール #必要なパッケージをロード library(param1, character.only=T) #param1で指定したパッケージの読み込み #probe IDとGene symbolとの対応関係を含む情報を入手 hoge <- sub(".db", param2, param1) #用いたいオブジェクト名情報を取得(rat2302SYMBOLに相当) hoge <- eval(parse(text=hoge)) #hogeを文字列としてではなくオブジェクトとして取り扱う symbols <- unlist(as.list(hoge)) #全31099 probesに対応するGeneSymbol(SYMBOL)情報を抽出し、symbolsに格納 unique_sym <- unique(symbols) #non-redundantなGeneSymbol(SYMBOL)情報を抽出し、unique_symに格納 unique_sym <- unique_sym[unique_sym != ""]#unique_symの中から、Gene symbolがないものを除く unique_sym <- unique_sym[!is.na(unique_sym)]#unique_symの中から、Gene symbolが"NA"のものを除く unique_sym <- unique_sym[!is.nan(unique_sym)]#unique_symの中から、Gene symbolが"NaN"のものを除く #本番 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み hoge <- NULL #最終的に欲しい情報を格納するためのプレースホルダ for(i in 1:length(unique_sym)){ #non-redundant gene symbol数分だけループを回す hoge <- rbind(hoge, apply(data[which(symbols == unique_sym[i]),], 2, param, na.rm=TRUE))#dataの中からi番目のgene symbolと同じprobesを全て抽出し、その平均値(mean)をhogeの一番下の行に追加 } #non-redundant gene symbol数分だけループを回す rownames(hoge) <- unique_sym #non-redundant gene symbolsをhogeの行の名前として利用 #ファイルに保存 tmp <- cbind(rownames(hoge), hoge) #遺伝子IDの列を行列hogeの左端に挿入し、結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
5. サンプルデータ18のsample18_5vs5.txtの場合:
入力ファイル中の4列目の情報をもとに、エクソンごとに分かれている同じ遺伝子のものをまとめています。同じ遺伝子上の複数のエクソンのstrand情報が+と-両方ある場合にはエラーを吐くようにしています。以下は入力と出力のイメージです。
入力:

出力:

in_f <- "sample18_5vs5.txt" #入力ファイルを指定してin_fに格納 out_f <- "hoge5.txt" #出力ファイル名を指定してout_fに格納 #データファイルの読み込み data <- read.table(in_f, header=TRUE, sep="\t", quote="")#in_fで指定したファイルの読み込み #genenameに相当する4列目の情報を抽出して加工("-ex"よりも左側の文字列のみ抽出) hoge <- strsplit(as.character(data[,4]), "-ex", fixed=TRUE)#data[,param]を文字列に変換し、"-ex"で区切った結果をリスト形式でhogeに格納 genename <- unlist(lapply(hoge, "[[", 1))#hogeのリスト中の1番目の要素("-ex"で区切った左側部分に相当)のみ抽出してgenenameに格納 unique_genename <- unique(genename) #non-redundantなgenename情報を抽出し、unique_genenameに格納 #1,6列目の情報(chrとstrand)はそのまま、5, 7-16列の情報(lengthとカウントデータ)のみsumしたいので、それぞれをサブセットに分ける sub1 <- data[,c(1,6)] #1,6列目の情報のみ抽出しsub1に格納 sub2 <- data[,c(5,7:16)] #5,7-16列目の情報のみ抽出しsub2に格納 out <- NULL #最終的に欲しい情報を格納するためのプレースホルダ for(i in 1:length(unique_genename)){ #unique_genenameの要素数分だけループを回す out_sub1 <- apply(sub1[which(genename == unique_genename[i]),], 2, unique, na.rm=TRUE)#sub1のところは、複数エクソンの場合は同じ情報がエクソン数分だけあることになるので、unique関数を実行した結果をout_sub1に格納 out_sub2 <- apply(sub2[which(genename == unique_genename[i]),], 2, sum, na.rm=TRUE)#sub2のところでは、複数エクソンの場合にsum関数を実行した結果(和をとった結果)をout_sub2に格納 out <- rbind(out, c(out_sub1, unique_genename[i], out_sub2))#「out_sub1, unique_genename[i], out_sub2」の順番で行列outの下に結果をどんどん追加 } write.table(out, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
6. サンプルデータ18のsample18_5vs5.txtの場合:
入力ファイル中の4列目の情報をもとに、エクソンごとに分かれている同じ遺伝子のものをまとめています。同じ遺伝子上の複数のエクソンのstrand情報が+と-両方ある場合には「2」を、そうでない場合には「1」としたベクトルを最初の一列目に追加で出力するようにしています。 以下は入力と出力のイメージです。
入力:

出力:

in_f <- "sample18_5vs5.txt" #入力ファイルを指定してin_fに格納 out_f <- "hoge6.txt" #出力ファイル名を指定してout_fに格納 #データファイルの読み込み data <- read.table(in_f, header=TRUE, sep="\t", quote="")#in_fで指定したファイルの読み込み #genenameに相当する4列目の情報を抽出して加工("-ex"よりも左側の文字列のみ抽出) hoge <- strsplit(as.character(data[,4]), "-ex", fixed=TRUE)#data[,param]を文字列に変換し、"-ex"で区切った結果をリスト形式でhogeに格納 genename <- unlist(lapply(hoge, "[[", 1))#hogeのリスト中の1番目の要素("-ex"で区切った左側部分に相当)のみ抽出してgenenameに格納 unique_genename <- unique(genename) #non-redundantなgenename情報を抽出し、unique_genenameに格納 #1,6列目の情報(chrとstrand)はそのまま、5, 7-16列の情報(lengthとカウントデータ)のみsumしたいので、それぞれをサブセットに分ける sub1 <- data[,c(1,6)] #1,6列目の情報のみ抽出しsub1に格納 sub2 <- data[,c(5,7:16)] #5,7-16列目の情報のみ抽出しsub2に格納 out <- NULL #最終的に欲しい情報を格納するためのプレースホルダ for(i in 1:length(unique_genename)){ #unique_genenameの要素数分だけループを回す tmp <- unlist(apply(sub1[which(genename == unique_genename[i]),], 2, unique, na.rm=TRUE))#sub1のところは、複数エクソンの場合は同じ情報がエクソン数分だけあることになるはずであるが、そうでない可能性があるときに見つけられるようにしている out_flag <- length(tmp) #ベクトルtmpの要素数をout_flagに格納(通常はtmpの要素数が2だが、3以上のものを検出するのが目的) out_sub1 <- tmp[1:2] #どんな状況になっていようと、とにかくベクトルtmpの最初の二つの要素を出力すべくout_sub1に格納 out_sub2 <- apply(sub2[which(genename == unique_genename[i]),], 2, sum, na.rm=TRUE)#sub2のところでは、複数エクソンの場合にsum関数を実行した結果(和をとった結果)をout_sub2に格納 out <- rbind(out, c(out_flag, out_sub1, unique_genename[i], out_sub2))#「out_sub1, unique_genename[i], out_sub2」の順番で行列outの下に結果をどんどん追加 } write.table(out, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
7. サンプルデータ20の31,099 probesets×24 samplesのRMA-preprocessedデータ(data_rma_2.txt)の場合:
Affymetrix Rat Genome 230 2.0 Arrayを用いて得られたNakai et al., BBB, 2008のデータです。
イントロ | アノテーション情報取得 | Rのパッケージ*.dbからを参考にして得られたprobe IDとEntrez IDとの対応関係を含む情報を利用するやり方です。 パッケージのダウンロードで時間がかかるかもしれません。"SYMBOL"や"ENTREZID"以外には、 "ACCNUM", "REFSEQ", "UNIGENE", "ENSEMBL", "ENSEMBLPROT", "ENSEMBLTRANS", "GENENAME", "PFAM", "PROSITE"などが指定可能です。
in_f <- "data_rma_2.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge7.txt" #出力ファイル名を指定してout_fに格納 param <- mean #代表値を指定 param1 <- "rat2302.db" #パッケージ名を指定 param2 <- "ENTREZID" #欲しいアノテーション情報を指定(記述可能なリストは以下のkeytypes(dbname)から取得可能) #必要なパッケージのインストール(利用したいパッケージが既に存在していれば2回目以降は必要なし) source("http://bioconductor.org/biocLite.R")#指定したパッケージのインストール biocLite(param1, suppressUpdates=TRUE) #指定したパッケージのインストール #必要なパッケージをロード library(param1, character.only=T) #param1で指定したパッケージの読み込み #probe IDとGene symbolとの対応関係を含む情報を入手 hoge <- sub(".db", param2, param1) #用いたいオブジェクト名情報を取得(rat2302SYMBOLに相当) hoge <- eval(parse(text=hoge)) #hogeを文字列としてではなくオブジェクトとして取り扱う symbols <- unlist(as.list(hoge)) #全31099 probesに対応するGeneSymbol(SYMBOL)情報を抽出し、symbolsに格納 unique_sym <- unique(symbols) #non-redundantなGeneSymbol(SYMBOL)情報を抽出し、unique_symに格納 unique_sym <- unique_sym[unique_sym != ""]#unique_symの中から、Gene symbolがないものを除く unique_sym <- unique_sym[!is.na(unique_sym)]#unique_symの中から、Gene symbolが"NA"のものを除く unique_sym <- unique_sym[!is.nan(unique_sym)]#unique_symの中から、Gene symbolが"NaN"のものを除く #本番 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み hoge <- NULL #最終的に欲しい情報を格納するためのプレースホルダ for(i in 1:length(unique_sym)){ #non-redundant gene symbol数分だけループを回す hoge <- rbind(hoge, apply(data[which(symbols == unique_sym[i]),], 2, param, na.rm=TRUE))#dataの中からi番目のgene symbolと同じprobesを全て抽出し、その平均値(mean)をhogeの一番下の行に追加 } #non-redundant gene symbol数分だけループを回す rownames(hoge) <- unique_sym #non-redundant gene symbolsをhogeの行の名前として利用 #ファイルに保存 tmp <- cbind(rownames(hoge), hoge) #遺伝子IDの列を行列hogeの左端に挿入し、結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
8. サンプルデータ5の22,283 probesets×36 samplesのRMA-preprocessedデータ(sample5.txt)の場合:
Affymetrix Human Genome U133A Array (GPL96)を用いて得られたGe et al., Genomics, 2005のデータです。
イントロ | アノテーション情報取得 | Rのパッケージ*.dbからを参考にして得られたprobe IDとEntrez IDとの対応関係を含む情報を利用するやり方です。 パッケージのダウンロードで時間がかかるかもしれません。"SYMBOL"や"ENTREZID"以外には、 "ACCNUM", "REFSEQ", "UNIGENE", "ENSEMBL", "ENSEMBLPROT", "ENSEMBLTRANS", "GENENAME", "PFAM", "PROSITE"などが指定可能です。
in_f <- "sample5.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge8.txt" #出力ファイル名を指定してout_fに格納 param <- mean #代表値を指定 param1 <- "hgu133a.db" #パッケージ名を指定 param2 <- "ENTREZID" #欲しいアノテーション情報を指定(記述可能なリストは以下のkeytypes(dbname)から取得可能) #必要なパッケージのインストール(利用したいパッケージが既に存在していれば2回目以降は必要なし) source("http://bioconductor.org/biocLite.R")#指定したパッケージのインストール biocLite(param1, suppressUpdates=TRUE) #指定したパッケージのインストール #必要なパッケージをロード library(param1, character.only=T) #param1で指定したパッケージの読み込み #probe IDとGene symbolとの対応関係を含む情報を入手 hoge <- sub(".db", param2, param1) #用いたいオブジェクト名情報を取得(rat2302SYMBOLに相当) hoge <- eval(parse(text=hoge)) #hogeを文字列としてではなくオブジェクトとして取り扱う symbols <- unlist(as.list(hoge)) #全31099 probesに対応するGeneSymbol(SYMBOL)情報を抽出し、symbolsに格納 unique_sym <- unique(symbols) #non-redundantなGeneSymbol(SYMBOL)情報を抽出し、unique_symに格納 unique_sym <- unique_sym[unique_sym != ""]#unique_symの中から、Gene symbolがないものを除く unique_sym <- unique_sym[!is.na(unique_sym)]#unique_symの中から、Gene symbolが"NA"のものを除く unique_sym <- unique_sym[!is.nan(unique_sym)]#unique_symの中から、Gene symbolが"NaN"のものを除く #本番 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み hoge <- NULL #最終的に欲しい情報を格納するためのプレースホルダ for(i in 1:length(unique_sym)){ #non-redundant gene symbol数分だけループを回す hoge <- rbind(hoge, apply(data[which(symbols == unique_sym[i]),], 2, param, na.rm=TRUE))#dataの中からi番目のgene symbolと同じprobesを全て抽出し、その平均値(mean)をhogeの一番下の行に追加 } #non-redundant gene symbol数分だけループを回す rownames(hoge) <- unique_sym #non-redundant gene symbolsをhogeの行の名前として利用 #ファイルに保存 tmp <- cbind(rownames(hoge), hoge) #遺伝子IDの列を行列hogeの左端に挿入し、結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
解析 | 基礎 | 共通遺伝子の抽出
「1列目:遺伝子名、2列目:数値」からなる二つのファイル(genelist_A.txtとgenelist_B.txt;いずれもヘッダー行を含む)があったとします。
そして、同じ遺伝子名のところの数値は同じだったとします。このような前提で二つのファイルで共通して含まれる遺伝子の情報のみ抽出したいときに利用します。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し、以下をコピペ
1. genelist_A.txtとgenelist_B.txt(いずれもヘッダー行を含む)の場合:
in_f1 <- "genelist_A.txt" #入力ファイル名を指定してin_f1に格納 in_f2 <- "genelist_B.txt" #入力ファイル名を指定してin_f2に格納 out_f <- "hoge.txt" #出力ファイル名を指定してout_fに格納 #データファイルの読み込み data1 <- read.table(in_f1, header=TRUE, row.names=1, sep="\t", quote="")#in_f1で指定したファイルの読み込み data2 <- read.table(in_f2, header=TRUE, row.names=1, sep="\t", quote="")#in_f2で指定したファイルの読み込み #本番 common <- intersect(rownames(data1), rownames(data2))#二つの遺伝子名のベクトル同士の積集合(intersection)をcommonに格納 obj <- is.element(rownames(data1), common)#rownames(data1)で表されるベクトル中の各要素がベクトルcommon中に含まれるか否かの情報をobjに格納(data1ではなくdata2のほうでもよい) out <- data1[obj,] #objがTRUEとなる行のみ抽出した結果をoutに格納 names(out) <- rownames(data1)[obj] #行列outに行名を付加している #ファイルに保存 tmp <- cbind(names(out), out) #行の名前、outを列ベクトル単位で結合し、結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
解析 | 基礎 | ベクトル間の距離
二つのベクトル間の距離を定義する方法は多数存在します。ここでは10 genes ×2 samplesのデータファイル(sample19.txt)を読み込んで二つのサンプル間の距離をいくつかの方法で算出します。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し、以下をコピペ
1. 10 genes ×2 samplesのデータファイル(sample19.txt)の場合:
in_f <- "sample19.txt" #入力ファイル名を指定してin_fに格納 #データファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 dist(t(data), method="euclidean") #ユークリッド(Euclidean)距離 dist(t(data), method="manhattan") #マンハッタン(Manhattan)距離 dist(t(data), method="maximum") #チェビシェフ(Chebyshev)距離 dist(t(data), method="canberra") #キャンベラ(Canberra)距離 1 - cor(data, method="pearson") #1 - Pearson相関係数 dist(t(data), method="binary") #ハミング(Hamming)距離 dist(t(data), method="minkowski") #ミンコフスキー(Minkowski)距離 1 - cor(data, method="spearman") #1 - Spearman相関係数
解析 | 基礎 | 遺伝子ごとの各種要約統計量の算出
遺伝子発現行列に対して、一つ一つの遺伝子(行)に対して、様々な基本的な情報を得たい場合に利用します。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し、以下をコピペ
1. 6 genes × 11 samplesのデータファイル(sample2.txt)の場合:
平均発現量を調べるやり方です。
in_f <- "sample2.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge1.txt" #出力ファイル名を指定してout_fに格納 #データファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み out <- apply(data, 1, mean) #各行の平均値(mean)をoutに格納 #ファイルに保存 tmp <- cbind(rownames(data), data, out)#行の名前、data、outを列ベクトル単位で結合し、結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
2. 6 genes × 11 samplesのデータファイル(sample2.txt)の場合:
中央値(median)を調べるやり方です。
in_f <- "sample2.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge2.txt" #出力ファイル名を指定してout_fに格納 #データファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み out <- apply(data, 1, median) #各行の中央値(median)をoutに格納 #ファイルに保存 tmp <- cbind(rownames(data), data, out)#行の名前、data、outを列ベクトル単位で結合し、結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
3. 6 genes × 11 samplesのデータファイル(sample2.txt)の場合:
重みつき平均(Tukey biweighted mean)を調べるやり方です。
in_f <- "sample2.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge3.txt" #出力ファイル名を指定してout_fに格納 #必要なパッケージをロード library(affy) #tukey.biweight関数が含まれているaffyパッケージの読み込み #データファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み out <- apply(data, 1, tukey.biweight) #各行のtukey.biweight値をoutに格納 #ファイルに保存 tmp <- cbind(rownames(data), data, out)#行の名前、data、outを列ベクトル単位で結合し、結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
解析 | 基礎 | 最大発現量を示す組織の同定
遺伝子発現行列に対して、一つ一つの遺伝子(行)に対して、様々な基本的な情報を得たい場合に利用します。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し、以下をコピペ
1. 6 genes × 11 samplesのデータファイル(sample2.txt)の場合:
遺伝子ごとに最大発現量を示す組織名をリストアップするやり方です。
in_f <- "sample2.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge1.txt" #出力ファイル名を指定してout_fに格納 #データファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 out <- colnames(data)[max.col(data)] #最大発現量を示す組織名outに格納 #ファイルに保存 tmp <- cbind(rownames(data), data, out)#入力データの右側にoutの情報を結合した結果をtmpに格納。 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
2. 6 genes × 11 samplesのデータファイル(sample2.txt)の場合:
遺伝子ごとに最大発現量を示す組織名を組織順にソートするやり方です。
in_f <- "sample2.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge2.txt" #出力ファイル名を指定してout_fに格納 #データファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 out <- colnames(data)[max.col(data)] #最大発現量を示す組織名outに格納 #ファイルに保存 tmp <- cbind(rownames(data), data, out)#入力データの右側にoutの情報を結合した結果をtmpに格納。 tmp2 <- tmp[order(max.col(data)),] #最大発現量を示す組織のシリアル番号順にソートした結果をtmp2に格納 write.table(tmp2, out_f, sep="\t", append=F, quote=F, row.names=F)#tmp2の中身を指定したファイル名で保存
解析 | 基礎 | 似た発現パターンを持つ遺伝子の同定
いわゆるパターンマッチング法(or テンプレートマッチング法; pattern matching; template matching)を適用して、"理想的なパターン" or "指定した遺伝子の発現パターン"に似た発現パターンを持つ遺伝子を検出(ランキング)します。ここでは、
- 指定した組織で理想的な特異的発現パターンを示す上位X個を得たい場合
- 上位X個ではなく似ている順に全遺伝子をソートした結果を得たい場合
- 指定した遺伝子の発現パターンに似た発現パターンを示す上位X個を得たい場合
の三つのやり方について紹介します。
類似度を計算する際に、
- 発現データ(遺伝子発現ベクトル)をあらかじめスケーリングするかしない(none)か?するとしたらどのようなスケーリング(range (各遺伝子のシグナル強度の範囲を0-1にする) or zscore (各遺伝子のシグナル強度の平均を0標準偏差を1にする))を行うか?
- 距離をどのような方法(euclidean, maximum, manhattan, canberra, correlation, binary)で定義するか?
も指定する必要があります。私は距離を普段から「1 - 相関係数」で定義しているので、それに相当するcorrelationを頻用します。また、スケーリングはやりません(none)。
「ファイル」−「ディレクトリの変更」で解析したいファイル(sample5.txt)を置いてあるディレクトリに移動し、以下をコピペ
1. 指定した組織で選択的(特異的)に発現する遺伝子群の上位10個(X=10)を得たい場合:
ここでは、予め作成した「心臓特異的発現パターン」を示す遺伝子群を抽出するための"理想的なパターン(テンプレート)"
を含むファイルGDS1096_cl_heart.txtを読み込んで、
発現パターンが似ている上位X個を二つのファイルdata_topranked.txt(発現データ含む)と
data_topranked_ID.txt(発現データ含まず遺伝子IDのみ)に保存するやり方を示します。
(発現ベクトルのスケーリングはせず(none)、
類似度は「1 - 相関係数」(correlation)で定義)
in_f1 <- "sample5.txt" #入力ファイル名(発現データ)を指定してin_f1に格納 in_f2 <- "GDS1096_cl_heart.txt" #入力ファイル名(テンプレート情報)を指定してin_f2に格納 out_f1 <- "data_torranded.txt" #出力ファイル名(発現データ含むほう)を指定 out_f2 <- "data_topranked_ID.txt" #出力ファイル名(遺伝子IDのみのほう)を指定 param1 <- 10 #上位X個のXを指定 param2 <- "none" #類似度計算前の発現データのスケーリング法を指定 param3 <- "correlation" #距離を定義する方法を指定 #必要なパッケージをロード library(genefilter) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f1, header=TRUE, row.names=1, sep="\t", quote="")#in_f1で指定したファイルの読み込み data <- as.matrix(data) #as.matrixの意味は、「データの型を"行列として(as matrix)"dataに格納せよ」です。(read.tableで読み込んで得られたdataの型は"データフレーム"のため) data_cl <- read.table(in_f2, sep="\t", quote="")#in_f2で指定したファイルの読み込み template <- data_cl[,2] #バイナリ(0 or 1)情報(2列目)のみ抽出し、templateに格納 template #バイナリ(0 or 1)情報の確認 #本番 tmp <- rbind(data, template) #templateというテンプレートパターンを行列dataの最後の行に追加 template_posi <- which(rownames(tmp) == "template")#行のラベル情報が"template"に相当する行番号をtemplate_posiに格納 closeg <- genefinder(tmp, template_posi, param1, scale=param2, method=param3)#上位"param1"個の情報をclosegに格納 closeg[[1]]$indices #上位"param1"個の行番号を表示 closeg[[1]]$dists #上位"param1"個の類似度を表示 topranked <- tmp[closeg[[1]]$indices,] #上位"param1"個の遺伝子発現データを抽出し、toprankedに格納 #ファイルに保存 tmp2 <- cbind(rownames(topranked), topranked)#遺伝子IDの列を行列toprankedの左端に挿入し、結果をtmp2に格納 write.table(tmp2, out_f1, sep="\t", append=F, quote=F, row.names=F)#tmp2の中身を指定したファイル名で保存 write.table(rownames(topranked), out_f2, sep="\t", append=F, quote=F, row.names=F, col.names=F)#遺伝子IDに関する情報のみ、指定したファイル名で保存 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
2. 似ている順に全遺伝子をソートした結果を得たい場合:
ここでは、予め作成した「心臓特異的発現パターン」を示す遺伝子群を抽出するための
"理想的なパターン(テンプレート)"を含むファイルGDS1096_cl_heart.txtを読み込んで、
「心臓特異的発現パターン」に似ている順に全遺伝子をソートした二つのファイル
data_topranked.txt(発現データ含む)とdata_topranked_ID.txt(発現データ含まず遺伝子IDのみ)
に保存するやり方を示します。
(発現ベクトルをZスケーリング(zscore)し、類似度は「1 - 相関係数」(correlation)で定義)
in_f1 <- "sample5.txt" #入力ファイル名(発現データ)を指定してin_f1に格納 in_f2 <- "GDS1096_cl_heart.txt" #入力ファイル名(テンプレート情報)を指定してin_f2に格納 out_f1 <- "data_torranded.txt" #出力ファイル名(発現データ含むほう)を指定 out_f2 <- "data_topranked_ID.txt" #出力ファイル名(遺伝子IDのみのほう)を指定 param2 <- "zscore" #類似度計算前の発現データのスケーリング法を指定 param3 <- "correlation" #距離を定義する方法を指定 #必要なパッケージをロード library(genefilter) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f1, header=TRUE, row.names=1, sep="\t", quote="")#入力ファイル1を読み込んでdataに格納 data <- as.matrix(data) #as.matrixの意味は、「データの型を"行列として(as matrix)"dataに格納せよ」です。(read.tableで読み込んで得られたdataの型は"データフレーム"のため) data_cl <- read.table(in_f2, sep="\t", quote="")#入力ファイル2を読み込んでdata_clに格納 template <- data_cl[,2] #バイナリ(0 or 1)情報(2列目)のみ抽出し、templateに格納 template #バイナリ(0 or 1)情報の確認 #本番 tmp <- rbind(data, template) #templateというテンプレートパターンを行列dataの最後の行に追加 template_posi <- which(rownames(tmp) == "template")#行のラベル情報が"template"に相当する行番号をtemplate_posiに格納 param1 <- nrow(data) #遺伝子数をparam1に格納 closeg <- genefinder(tmp, template_posi, param1, scale=param2, method=param3)#特異的発現の度合いでランキングされた結果をclosegに格納 topranked <- tmp[closeg[[1]]$indices,] #特異的発現の度合いでランキングされた遺伝子発現データをtoprankedに格納 #ファイルに保存 tmp2 <- cbind(rownames(topranked), topranked)#遺伝子IDの列を行列toprankedの左端に挿入し、結果をtmp2に格納 write.table(tmp2, out_f1, sep="\t", append=F, quote=F, row.names=F)#tmp2の中身を指定したファイル名で保存 write.table(rownames(topranked), out_f2, sep="\t", append=F, quote=F, row.names=F, col.names=F)#遺伝子IDに関する情報のみ、指定したファイル名で保存
3. 遺伝子ID: 207003_atの遺伝子発現プロファイルと発現パターンが似ている上位5個をリストアップしたい場合:
(発現ベクトルをRangeスケーリング(range)し、類似度はマンハッタン距離(manhattan)で定義)
in_f <- "sample5.txt" #入力ファイル名を指定してin_fに格納 out_f1 <- "data_torranded.txt" #出力ファイル名(発現データ含むほう)を指定 out_f2 <- "data_topranked_ID.txt" #出力ファイル名(遺伝子IDのみのほう)を指定 param1 <- 5 #上位X個のXを指定 param2 <- "range" #類似度計算前の発現データのスケーリング法を指定 param3 <- "manhattan" #距離を定義する方法を指定 param4 <- "207003_at" #遺伝子IDを指定 #必要なパッケージをロード library(genefilter) #パッケージの読み込み #データファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data <- as.matrix(data) #as.matrixの意味は、「データの型を"行列として(as matrix)"dataに格納せよ」です。(read.tableで読み込んで得られたdataの型は"データフレーム"のため) #本番 template_posi <- which(rownames(data) == param4)#param4で指定した遺伝子IDに相当する行番号をtemplate_posiに格納 closeg <- genefinder(data, template_posi, param1, scale=param2, method=param3)#上位"param1"個の情報をclosegに格納 topranked <- data[closeg[[1]]$indices,]#上位"param1"個の遺伝子発現データを抽出し、toprankedに格納 #ファイルに保存 tmp2 <- cbind(rownames(topranked), topranked)#遺伝子IDの列を行列toprankedの左端に挿入し、結果をtmp2に格納 write.table(tmp2, out_f1, sep="\t", append=F, quote=F, row.names=F)#tmp2の中身を指定したファイル名で保存 write.table(rownames(topranked), out_f2, sep="\t", append=F, quote=F, row.names=F, col.names=F)#遺伝子IDに関する情報のみ、指定したファイル名で保存
4. (ヘッダー行を除く)15987行目(ID_REF: "216617_s_at"の行に相当)の遺伝子発現プロファイルと
発現パターンが似ている上位10個をリストアップしたい場合:
(発現ベクトルをZスケーリング(zscore)し、類似度は「1 - 相関係数」(correlation)で定義)
in_f <- "sample5.txt" #入力ファイル名を指定してin_fに格納 out_f1 <- "data_torranded.txt" #出力ファイル名(発現データ含むほう)を指定してout_f1に格納 out_f2 <- "data_topranked_ID.txt" #出力ファイル名(遺伝子IDのみのほう)を指定してout_f2に格納 param1 <- 10 #上位X個のXを指定 param2 <- "zscore" #類似度計算前の発現データのスケーリング法を指定 param3 <- "correlation" #距離を定義する方法を指定 param4 <- 15987 #目的遺伝子の行番号を指定 #必要なパッケージをロード library(genefilter) #パッケージの読み込み #データファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data <- as.matrix(data) #as.matrixの意味は、「データの型を"行列として(as matrix)"dataに格納せよ」です。(read.tableで読み込んで得られたdataの型は"データフレーム"のため) #本番 closeg <- genefinder(data, param4, param1, scale=param2, method=param3)#上位"param1"個の情報をclosegに格納 topranked <- data[closeg[[1]]$indices,]#上位"param1"個の遺伝子発現データを抽出し、toprankedに格納 #ファイルに保存 tmp2 <- cbind(rownames(topranked), topranked)#遺伝子IDの列を行列toprankedの左端に挿入し、結果をtmp2に格納 write.table(tmp2, out_f1, sep="\t", append=F, quote=F, row.names=F)#tmp2の中身を指定したファイル名で保存 write.table(rownames(topranked), out_f2, sep="\t", append=F, quote=F, row.names=F, col.names=F)#遺伝子IDに関する情報のみ、指定したファイル名で保存
解析 | 基礎 | 平均-分散プロット
RNA-seqのカウントデータはTechnical replicatesのデータがポアソン分布(Poisson distribution)に、そしてBiological replicatesのデータが負の二項分布に従うことを報告しています。 そして、マイクロアレイデータも似たような平均-分散の形状を示すという報告もあります(Subramaniam and Hsiao, 2012)。 ここでは、マイクロアレイデータを読み込んで平均-分散プロットを作成します。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し以下をコピペ。
1. サンプルデータ24の31,099 probesets×10 samplesのMAS5-preprocessedデータ(data_GSE30533_mas.txt)の場合:
Kamei et al., PLoS One, 2013のデータです。
in_f <- "data_GSE30533_mas.txt" #入力ファイル名を指定してin_fに格納 out_f1 <- "hoge1_G1.txt" #出力ファイル名を指定してout_f1に格納 out_f2 <- "hoge1_G1.png" #出力ファイル名を指定してout_f2に格納 out_f3 <- "hoge1_G2.txt" #出力ファイル名を指定してout_f3に格納 out_f4 <- "hoge1_G2.png" #出力ファイル名を指定してout_f4に格納 out_f5 <- "hoge1_all.png" #出力ファイル名を指定してout_f5に格納 param_G1 <- 5 #G1群のサンプル数を指定 param_G2 <- 5 #G2群のサンプル数を指定 param_fig <- c(380, 420) #ファイル出力時の横幅と縦幅を指定(単位はピクセル) param_range <- c(1e-02, 1e+08) #M-A plot上での軸の数値範囲を指定 #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #前処理(対数変換後のデータなので、オリジナルスケールに変換したのち、群ごとに分割) data <- 2^data #データ変換 data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 G1 <- data[,data.cl==1] #G1群のデータのみ抽出している G2 <- data[,data.cl==2] #G2群のデータのみ抽出している #本番(Mean-Variance plotなど; G1群) hoge <- G1 #G1オブジェクトをhogeに格納 MEAN <- apply(hoge, 1, mean) #各行の平均を計算した結果をMEANに格納 VARIANCE <- apply(hoge, 1, var) #各行の分散を計算した結果をVARIANCEに格納 tmp <- cbind(rownames(data), data[,data.cl==1], hoge, MEAN, VARIANCE)#保存したい情報をtmpに格納 write.table(tmp, out_f1, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存 png(out_f2, pointsize=13, width=param_fig[1], height=param_fig[2])#出力ファイルの各種パラメータを指定 plot(MEAN, VARIANCE, log="xy", pch=20, cex=.1,#プロット xlim=param_range, ylim=param_range, col="blue")#プロット grid(col="gray", lty="dotted") #指定したパラメータでグリッドを表示 abline(a=0, b=1, col="gray") #y=xの直線を指定した色で追加(y=a+bxのa=0, b=1) legend("topright", "G1", col="blue", pch=20)#凡例を作成している hoge <- hoge[apply(hoge, 1, var) > 0,] #回帰分析のときにエラーが出ないように分散>0のもののみ抽出しているだけ MEAN <- apply(hoge, 1, mean) #各行の平均を計算した結果をMEANに格納 VARIANCE <- apply(hoge, 1, var) #各行の分散を計算した結果をVARIANCEに格納 hoge <- as.data.frame(cbind(MEAN, VARIANCE))#回帰分析(regression analysis)を行うためののおまじない(1列目がMEAN, 2列目がVARIANCEならなる行列を作成したあとデータフレーム形式にした結果をhogeに格納) out <- lm(VARIANCE~MEAN, data=log10(hoge))#独立変数(説明変数)をMEAN, 従属変数(目的変数)をVARIANCEとしてlog10変換したデータの線形回帰を行った結果をoutに格納 abline(out, col="black") #回帰直線を追加 out #outの簡単な中身を表示(切片(Intercept)が-0.001173, 傾き(MEAN)が1.349519であることがわかる。つまり、y=a+bxのaが切片、bが傾きに相当する) summary(out) #回帰分析結果outのもう少し詳細な結果を表示している(Multiple R-squared(決定係数)の値が0.8149と1に相当近い値が得られていることから線形回帰で十分よいfittingが得られていると判断できる。また、一番下のp-valueが限りなく0に近いことは、MEANという従属変数が不要であるという帰無仮説を棄却するに値する、つまり従属変数が独立変数によって説明可能であることを意味する) dev.off() #おまじない #本番(Mean-Variance plotなど; G2群) hoge <- G2 #G2オブジェクトをhogeに格納 MEAN <- apply(hoge, 1, mean) #各行の平均を計算した結果をMEANに格納 VARIANCE <- apply(hoge, 1, var) #各行の分散を計算した結果をVARIANCEに格納 tmp <- cbind(rownames(data), data[,data.cl==1], hoge, MEAN, VARIANCE)#保存したい情報をtmpに格納 write.table(tmp, out_f3, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存 png(out_f4, pointsize=13, width=param_fig[1], height=param_fig[2])#出力ファイルの各種パラメータを指定 plot(MEAN, VARIANCE, log="xy", pch=20, cex=.1,#プロット xlim=param_range, ylim=param_range, col="red")#プロット grid(col="gray", lty="dotted") #指定したパラメータでグリッドを表示 abline(a=0, b=1, col="gray") #y=xの直線を指定した色で追加(y=a+bxのa=0, b=1) legend("topright", "G2", col="red", pch=20)#凡例を作成している hoge <- hoge[apply(hoge, 1, var) > 0,] #回帰分析のときにエラーが出ないように分散>0のもののみ抽出しているだけ MEAN <- apply(hoge, 1, mean) #各行の平均を計算した結果をMEANに格納 VARIANCE <- apply(hoge, 1, var) #各行の分散を計算した結果をVARIANCEに格納 hoge <- as.data.frame(cbind(MEAN, VARIANCE))#回帰分析(regression analysis)を行うためののおまじない(1列目がMEAN, 2列目がVARIANCEならなる行列を作成したあとデータフレーム形式にした結果をhogeに格納) out <- lm(VARIANCE~MEAN, data=log10(hoge))#独立変数(説明変数)をMEAN, 従属変数(目的変数)をVARIANCEとしてlog10変換したデータの線形回帰を行った結果をoutに格納 abline(out, col="black") #回帰直線を追加 out #outの簡単な中身を表示(切片(Intercept)が-0.001173, 傾き(MEAN)が1.349519であることがわかる。つまり、y=a+bxのaが切片、bが傾きに相当する) summary(out) #回帰分析結果outのもう少し詳細な結果を表示している(Multiple R-squared(決定係数)の値が0.8149と1に相当近い値が得られていることから線形回帰で十分よいfittingが得られていると判断できる。また、一番下のp-valueが限りなく0に近いことは、MEANという従属変数が不要であるという帰無仮説を棄却するに値する、つまり従属変数が独立変数によって説明可能であることを意味する) dev.off() #おまじない #本番(Mean-Variance plot; G1 and G2両方) hoge <- G1 #G1オブジェクトをhogeに格納 MEAN <- apply(hoge, 1, mean) #各行の平均を計算した結果をMEANに格納 VARIANCE <- apply(hoge, 1, var) #各行の分散を計算した結果をVARIANCEに格納 png(out_f5, pointsize=13, width=param_fig[1], height=param_fig[2])#出力ファイルの各種パラメータを指定 plot(MEAN, VARIANCE, log="xy", pch=20, cex=.1, ann=F,#プロット xlim=param_range, ylim=param_range, col="blue")#プロット par(new=T) #図の重ね合わせをするという宣言 hoge <- G2 #G2オブジェクトをhogeに格納 MEAN <- apply(hoge, 1, mean) #各行の平均を計算した結果をMEANに格納 VARIANCE <- apply(hoge, 1, var) #各行の分散を計算した結果をVARIANCEに格納 plot(MEAN, VARIANCE, log="xy", pch=20, cex=.1,#プロット xlim=param_range, ylim=param_range, col="red")#プロット grid(col="gray", lty="dotted") #指定したパラメータでグリッドを表示 abline(a=0, b=1, col="gray") #y=xの直線を指定した色で追加(y=a+bxのa=0, b=1) legend("topright", c("G1", "G2"), col=c("blue", "red"), pch=20)#凡例を作成している dev.off() #おまじない
2. サンプルデータ20の31,099 probesets×24 samplesのRMA-preprocessedデータ(data_rma_2.txt)の場合:
Nakai et al., BBB, 2008のデータです。
(データを読み込んだ後に、最初の8列分(Brown adopise tissue)のみ抽出して
4 fed samples vs. 4 fasted samplesの2群間比較データとして取り扱っています)
in_f <- "data_rma_2.txt" #入力ファイル名を指定してin_fに格納 out_f1 <- "hoge2_G1.txt" #出力ファイル名を指定してout_f1に格納 out_f2 <- "hoge2_G1.png" #出力ファイル名を指定してout_f2に格納 out_f3 <- "hoge2_G2.txt" #出力ファイル名を指定してout_f3に格納 out_f4 <- "hoge2_G2.png" #出力ファイル名を指定してout_f4に格納 out_f5 <- "hoge2_all.png" #出力ファイル名を指定してout_f5に格納 param_G1 <- 4 #G1群(fed)のサンプル数を指定 param_G2 <- 4 #G2群(fasted)のサンプル数を指定 param_fig <- c(380, 420) #ファイル出力時の横幅と縦幅を指定(単位はピクセル) param_range <- c(1e-02, 1e+08) #M-A plot上での軸の数値範囲を指定 #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み colSums(data) #総リード数を表示 #前処理(対数変換後のデータなので、オリジナルスケールに変換している) data <- 2^data #データ変換 #前処理(最初の8列分のみ抽出したのち、群ごとのサブセットに分けている) data <- data[,1:8] #最初の8列分のデータのみ抽出している data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 G1 <- data[,data.cl==1] #G1群のデータのみ抽出している colSums(G1) #総リード数を表示 G2 <- data[,data.cl==2] #G2群のデータのみ抽出している colSums(G2) #総リード数を表示 #本番(Mean-Variance plotなど; G1群) hoge <- G1 #G1オブジェクトをhogeに格納 MEAN <- apply(hoge, 1, mean) #各行の平均を計算した結果をMEANに格納 VARIANCE <- apply(hoge, 1, var) #各行の分散を計算した結果をVARIANCEに格納 tmp <- cbind(rownames(data), data[,data.cl==1], hoge, MEAN, VARIANCE)#保存したい情報をtmpに格納 write.table(tmp, out_f1, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存 png(out_f2, pointsize=13, width=param_fig[1], height=param_fig[2])#出力ファイルの各種パラメータを指定 plot(MEAN, VARIANCE, log="xy", pch=20, cex=.1,#プロット xlim=param_range, ylim=param_range, col="blue")#プロット grid(col="gray", lty="dotted") #指定したパラメータでグリッドを表示 abline(a=0, b=1, col="gray") #y=xの直線を指定した色で追加(y=a+bxのa=0, b=1) legend("topright", "G1", col="blue", pch=20)#凡例を作成している hoge <- hoge[apply(hoge, 1, var) > 0,] #回帰分析のときにエラーが出ないように分散>0のもののみ抽出しているだけ MEAN <- apply(hoge, 1, mean) #各行の平均を計算した結果をMEANに格納 VARIANCE <- apply(hoge, 1, var) #各行の分散を計算した結果をVARIANCEに格納 hoge <- as.data.frame(cbind(MEAN, VARIANCE))#回帰分析(regression analysis)を行うためののおまじない(1列目がMEAN, 2列目がVARIANCEならなる行列を作成したあとデータフレーム形式にした結果をhogeに格納) out <- lm(VARIANCE~MEAN, data=log10(hoge))#独立変数(説明変数)をMEAN, 従属変数(目的変数)をVARIANCEとしてlog10変換したデータの線形回帰を行った結果をoutに格納 abline(out, col="black") #回帰直線を追加 out #outの簡単な中身を表示(切片(Intercept)が-0.001173, 傾き(MEAN)が1.349519であることがわかる。つまり、y=a+bxのaが切片、bが傾きに相当する) summary(out) #回帰分析結果outのもう少し詳細な結果を表示している(Multiple R-squared(決定係数)の値が0.8149と1に相当近い値が得られていることから線形回帰で十分よいfittingが得られていると判断できる。また、一番下のp-valueが限りなく0に近いことは、MEANという従属変数が不要であるという帰無仮説を棄却するに値する、つまり従属変数が独立変数によって説明可能であることを意味する) dev.off() #おまじない #本番(Mean-Variance plotなど; G2群) hoge <- G2 #G2オブジェクトをhogeに格納 MEAN <- apply(hoge, 1, mean) #各行の平均を計算した結果をMEANに格納 VARIANCE <- apply(hoge, 1, var) #各行の分散を計算した結果をVARIANCEに格納 tmp <- cbind(rownames(data), data[,data.cl==1], hoge, MEAN, VARIANCE)#保存したい情報をtmpに格納 write.table(tmp, out_f3, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存 png(out_f4, pointsize=13, width=param_fig[1], height=param_fig[2])#出力ファイルの各種パラメータを指定 plot(MEAN, VARIANCE, log="xy", pch=20, cex=.1,#プロット xlim=param_range, ylim=param_range, col="red")#プロット grid(col="gray", lty="dotted") #指定したパラメータでグリッドを表示 abline(a=0, b=1, col="gray") #y=xの直線を指定した色で追加(y=a+bxのa=0, b=1) legend("topright", "G2", col="red", pch=20)#凡例を作成している hoge <- hoge[apply(hoge, 1, var) > 0,] #回帰分析のときにエラーが出ないように分散>0のもののみ抽出しているだけ MEAN <- apply(hoge, 1, mean) #各行の平均を計算した結果をMEANに格納 VARIANCE <- apply(hoge, 1, var) #各行の分散を計算した結果をVARIANCEに格納 hoge <- as.data.frame(cbind(MEAN, VARIANCE))#回帰分析(regression analysis)を行うためののおまじない(1列目がMEAN, 2列目がVARIANCEならなる行列を作成したあとデータフレーム形式にした結果をhogeに格納) out <- lm(VARIANCE~MEAN, data=log10(hoge))#独立変数(説明変数)をMEAN, 従属変数(目的変数)をVARIANCEとしてlog10変換したデータの線形回帰を行った結果をoutに格納 abline(out, col="black") #回帰直線を追加 out #outの簡単な中身を表示(切片(Intercept)が-0.001173, 傾き(MEAN)が1.349519であることがわかる。つまり、y=a+bxのaが切片、bが傾きに相当する) summary(out) #回帰分析結果outのもう少し詳細な結果を表示している(Multiple R-squared(決定係数)の値が0.8149と1に相当近い値が得られていることから線形回帰で十分よいfittingが得られていると判断できる。また、一番下のp-valueが限りなく0に近いことは、MEANという従属変数が不要であるという帰無仮説を棄却するに値する、つまり従属変数が独立変数によって説明可能であることを意味する) dev.off() #おまじない #本番(Mean-Variance plot; G1 and G2両方) hoge <- G1 #G1オブジェクトをhogeに格納 MEAN <- apply(hoge, 1, mean) #各行の平均を計算した結果をMEANに格納 VARIANCE <- apply(hoge, 1, var) #各行の分散を計算した結果をVARIANCEに格納 png(out_f5, pointsize=13, width=param_fig[1], height=param_fig[2])#出力ファイルの各種パラメータを指定 plot(MEAN, VARIANCE, log="xy", pch=20, cex=.1, ann=F,#プロット xlim=param_range, ylim=param_range, col="blue")#プロット par(new=T) #図の重ね合わせをするという宣言 hoge <- G2 #G2オブジェクトをhogeに格納 MEAN <- apply(hoge, 1, mean) #各行の平均を計算した結果をMEANに格納 VARIANCE <- apply(hoge, 1, var) #各行の分散を計算した結果をVARIANCEに格納 plot(MEAN, VARIANCE, log="xy", pch=20, cex=.1,#プロット xlim=param_range, ylim=param_range, col="red")#プロット grid(col="gray", lty="dotted") #指定したパラメータでグリッドを表示 abline(a=0, b=1, col="gray") #y=xの直線を指定した色で追加(y=a+bxのa=0, b=1) legend("topright", c("G1", "G2"), col=c("blue", "red"), pch=20)#凡例を作成している dev.off() #おまじない
3. サンプルデータ20の31,099 probesets×24 samplesのMAS5-preprocessedデータ(data_mas.txt)の場合:
Nakai et al., BBB, 2008のデータです。
(データを読み込んだ後に、最初の8列分(Brown adopise tissue)のみ抽出して
4 fed samples vs. 4 fasted samplesの2群間比較データとして取り扱っています)
in_f <- "data_mas.txt" #入力ファイル名を指定してin_fに格納 out_f1 <- "hoge3_G1.txt" #出力ファイル名を指定してout_f1に格納 out_f2 <- "hoge3_G1.png" #出力ファイル名を指定してout_f2に格納 out_f3 <- "hoge3_G2.txt" #出力ファイル名を指定してout_f3に格納 out_f4 <- "hoge3_G2.png" #出力ファイル名を指定してout_f4に格納 out_f5 <- "hoge3_all.png" #出力ファイル名を指定してout_f5に格納 param_G1 <- 4 #G1群(fed)のサンプル数を指定 param_G2 <- 4 #G2群(fasted)のサンプル数を指定 param_fig <- c(380, 420) #ファイル出力時の横幅と縦幅を指定(単位はピクセル) param_range <- c(1e-02, 1e+08) #M-A plot上での軸の数値範囲を指定 #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み colSums(data) #総リード数を表示 #前処理(対数変換後のデータなので、オリジナルスケールに変換している) data <- 2^data #データ変換 #前処理(最初の8列分のみ抽出したのち、群ごとのサブセットに分けている) data <- data[,1:8] #最初の8列分のデータのみ抽出している data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 G1 <- data[,data.cl==1] #G1群のデータのみ抽出している colSums(G1) #総リード数を表示 G2 <- data[,data.cl==2] #G2群のデータのみ抽出している colSums(G2) #総リード数を表示 #本番(Mean-Variance plotなど; G1群) hoge <- G1 #G1オブジェクトをhogeに格納 MEAN <- apply(hoge, 1, mean) #各行の平均を計算した結果をMEANに格納 VARIANCE <- apply(hoge, 1, var) #各行の分散を計算した結果をVARIANCEに格納 tmp <- cbind(rownames(data), data[,data.cl==1], hoge, MEAN, VARIANCE)#保存したい情報をtmpに格納 write.table(tmp, out_f1, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存 png(out_f2, pointsize=13, width=param_fig[1], height=param_fig[2])#出力ファイルの各種パラメータを指定 plot(MEAN, VARIANCE, log="xy", pch=20, cex=.1,#プロット xlim=param_range, ylim=param_range, col="blue")#プロット grid(col="gray", lty="dotted") #指定したパラメータでグリッドを表示 abline(a=0, b=1, col="gray") #y=xの直線を指定した色で追加(y=a+bxのa=0, b=1) legend("topright", "G1", col="blue", pch=20)#凡例を作成している hoge <- hoge[apply(hoge, 1, var) > 0,] #回帰分析のときにエラーが出ないように分散>0のもののみ抽出しているだけ MEAN <- apply(hoge, 1, mean) #各行の平均を計算した結果をMEANに格納 VARIANCE <- apply(hoge, 1, var) #各行の分散を計算した結果をVARIANCEに格納 hoge <- as.data.frame(cbind(MEAN, VARIANCE))#回帰分析(regression analysis)を行うためののおまじない(1列目がMEAN, 2列目がVARIANCEならなる行列を作成したあとデータフレーム形式にした結果をhogeに格納) out <- lm(VARIANCE~MEAN, data=log10(hoge))#独立変数(説明変数)をMEAN, 従属変数(目的変数)をVARIANCEとしてlog10変換したデータの線形回帰を行った結果をoutに格納 abline(out, col="black") #回帰直線を追加 out #outの簡単な中身を表示(切片(Intercept)が-0.001173, 傾き(MEAN)が1.349519であることがわかる。つまり、y=a+bxのaが切片、bが傾きに相当する) summary(out) #回帰分析結果outのもう少し詳細な結果を表示している(Multiple R-squared(決定係数)の値が0.8149と1に相当近い値が得られていることから線形回帰で十分よいfittingが得られていると判断できる。また、一番下のp-valueが限りなく0に近いことは、MEANという従属変数が不要であるという帰無仮説を棄却するに値する、つまり従属変数が独立変数によって説明可能であることを意味する) dev.off() #おまじない #本番(Mean-Variance plotなど; G2群) hoge <- G2 #G2オブジェクトをhogeに格納 MEAN <- apply(hoge, 1, mean) #各行の平均を計算した結果をMEANに格納 VARIANCE <- apply(hoge, 1, var) #各行の分散を計算した結果をVARIANCEに格納 tmp <- cbind(rownames(data), data[,data.cl==1], hoge, MEAN, VARIANCE)#保存したい情報をtmpに格納 write.table(tmp, out_f3, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存 png(out_f4, pointsize=13, width=param_fig[1], height=param_fig[2])#出力ファイルの各種パラメータを指定 plot(MEAN, VARIANCE, log="xy", pch=20, cex=.1,#プロット xlim=param_range, ylim=param_range, col="red")#プロット grid(col="gray", lty="dotted") #指定したパラメータでグリッドを表示 abline(a=0, b=1, col="gray") #y=xの直線を指定した色で追加(y=a+bxのa=0, b=1) legend("topright", "G2", col="red", pch=20)#凡例を作成している hoge <- hoge[apply(hoge, 1, var) > 0,] #回帰分析のときにエラーが出ないように分散>0のもののみ抽出しているだけ MEAN <- apply(hoge, 1, mean) #各行の平均を計算した結果をMEANに格納 VARIANCE <- apply(hoge, 1, var) #各行の分散を計算した結果をVARIANCEに格納 hoge <- as.data.frame(cbind(MEAN, VARIANCE))#回帰分析(regression analysis)を行うためののおまじない(1列目がMEAN, 2列目がVARIANCEならなる行列を作成したあとデータフレーム形式にした結果をhogeに格納) out <- lm(VARIANCE~MEAN, data=log10(hoge))#独立変数(説明変数)をMEAN, 従属変数(目的変数)をVARIANCEとしてlog10変換したデータの線形回帰を行った結果をoutに格納 abline(out, col="black") #回帰直線を追加 out #outの簡単な中身を表示(切片(Intercept)が-0.001173, 傾き(MEAN)が1.349519であることがわかる。つまり、y=a+bxのaが切片、bが傾きに相当する) summary(out) #回帰分析結果outのもう少し詳細な結果を表示している(Multiple R-squared(決定係数)の値が0.8149と1に相当近い値が得られていることから線形回帰で十分よいfittingが得られていると判断できる。また、一番下のp-valueが限りなく0に近いことは、MEANという従属変数が不要であるという帰無仮説を棄却するに値する、つまり従属変数が独立変数によって説明可能であることを意味する) dev.off() #おまじない #本番(Mean-Variance plot; G1 and G2両方) hoge <- G1 #G1オブジェクトをhogeに格納 MEAN <- apply(hoge, 1, mean) #各行の平均を計算した結果をMEANに格納 VARIANCE <- apply(hoge, 1, var) #各行の分散を計算した結果をVARIANCEに格納 png(out_f5, pointsize=13, width=param_fig[1], height=param_fig[2])#出力ファイルの各種パラメータを指定 plot(MEAN, VARIANCE, log="xy", pch=20, cex=.1, ann=F,#プロット xlim=param_range, ylim=param_range, col="blue")#プロット par(new=T) #図の重ね合わせをするという宣言 hoge <- G2 #G2オブジェクトをhogeに格納 MEAN <- apply(hoge, 1, mean) #各行の平均を計算した結果をMEANに格納 VARIANCE <- apply(hoge, 1, var) #各行の分散を計算した結果をVARIANCEに格納 plot(MEAN, VARIANCE, log="xy", pch=20, cex=.1,#プロット xlim=param_range, ylim=param_range, col="red")#プロット grid(col="gray", lty="dotted") #指定したパラメータでグリッドを表示 abline(a=0, b=1, col="gray") #y=xの直線を指定した色で追加(y=a+bxのa=0, b=1) legend("topright", c("G1", "G2"), col=c("blue", "red"), pch=20)#凡例を作成している dev.off() #おまじない
解析 | クラスタリング | について
クラスタリング全般について、階層的・非階層的に分類できないものをまとめておきます。
R用:
R以外:
Review、ガイドライン、パイプライン系:
- 手法評価(performance measure; BHI and BSI):Datta and Datta, BMC Bioinformatics, 2006
- 手法評価(Self Organizing Tree Algorithm (SOTA)がHCやSOMに比べていいよ):Yin et al., BMC Bioinformatics, 2006
- 手法比較(類似度の定義の仕方など):Jaskowiak et al., BMC Bioinformatics, 2014
解析 | クラスタリング | 階層的 | について
とりあえず枠組みのみ。
R用:
- clusterStab:原著論文なし
- pvclust:Suzuki and Shimodaira, Bioinformatics, 2006
- dendextend (一般的な階層的クラスタリング系):Galili T, Bioinformatics, 2015
R以外:
Review、ガイドライン、パイプライン系:
以下は2009年頃書いた非常に古い記述内容なので、参考程度。
-
階層的クラスタリングは大きく二つの方法に分類可能です(Smolkin and Ghosh, 2003):
- agglomerative nesting method
- divisive analysis method
日本語だと1. 凝集法と2. 分割法、でしょうか。おそらくなじみ深いのは1.のagglomerative nesting methodのほうでしょう。
例えばn個の組織からなるマイクロアレイデータに対する組織間(サンプル間)クラスタリングの場合だと、以下のような感じになります。
- agglomerative nesting method:初期状態はn個の(各クラスターの構成要素が一つのサンプルしかない)クラスター(n singleton clusters)からスタート
- 全てのクラスター間の総当たりの距離行列を作成
- 最も距離が近い二つのクラスターを一つにまとめる
- 最終的に一つのクラスターになるまでa,bを繰り返す
- 2. divisive analysis method:初期状態は全nサンプルをまとめた一つのクラスターからスタート
- クラスターの中で、最も他のサンプル群から距離が離れたサンプルを分離し、"分裂グループ(splinter group)"に入れる
- オリジナルクラスター中の残りのサンプルに対して、新たに形成された分裂グループに近いものは入れる
(結果として二つのクラスターが形成される) - 各クラスターの直径(同じクラスター内の総当たりのサンプル間距離を計算し、最も遠い距離に相当)を計算し、どちらが大きいかを調べる
- 直径のより大きいほうのクラスターに対して、a-cを繰り返す
- a-dをn singleton clustersになるまで繰り返す
20090812現在、1.のAgglomerative nesting methodのやり方しかこのページにはありませんが、必要に応じて追加していく予定です。
-
(階層的)クラスタリングはこれまで、癌のサブタイプの発見などに威力を発揮してきました(Bittner et al., 2000)。 しかし、クラスタリングの一番の問題は興味あるクラスターが偶然では形成されない(されにくい)信頼できるクラスターかどうかの判断が難しいことだと思います。 p値のようなものがない、という理解でも差し支えありません。 それゆえ、このページでは、特に信頼できるクラスターがどれかを調べるためのやり方(pvclust)や、 適切なクラスター数および得られたクラスターの安定性を知るための方法(最適なクラスター数を見積る)の紹介を行っています。 この二つのやり方はいずれも基本的にサンプル間クラスタリングを例として挙げています。これはやはり、数百程度のサンプルのクラスタリングだとメモリ4GB程度でどうにかなるからです。
-
個人的には遺伝子間クラスタリングをやる意味はないと思っています。現実問題として、信頼できる遺伝子クラスターを得ることができないためです。 従来一つにまとめられていた癌のサブタイプの発見などを目的とするならば、 まずはpvclustか最適なクラスター数を見積るを行って、サブタイプがありそうかどうかを判断し、 例えば二つのサブタイプに分かれそうだという感じであれば、解析 | 発現変動 | 2群間 | 対応なし |についてなどで紹介している方法を適用して、候補サブタイプ間で発現の異なる遺伝子群の検出を行います。 当然、一連の作業中に遺伝子間クラスタリングを行うphaseはありません。
-
また、このページの項目名でいうところの"正規化"や"前処理"のどれを行うかによっても、得られるクラスタリングの結果(樹形図)が異なることにも注意が必要です。 これはクラスタリングの欠点の一つとも言えるのかもしれませんが、本来クラスタリングというのは"何の予断も持たずにとにかく似たものをどんどんまとめていく"ものなのですが、 多くの場合、例えば癌サンプル数十例と正常サンプル数十例のサンプル間クラスタリングを行う際、実際には、癌と正常組織が二群に分かれるのではないだろうかと事前に無意識のうちに期待します。 それゆえ、はっきりと二群に分かれない結果が得られるとがっかり...します。それでデータを取りなおしたり、都合の悪いサンプルの結果を難癖つけて排除...したがります。 これ以外の行動パターンとしては、正規化法Aを用いて得られた遺伝子発現行列のクラスタリング結果と正規化法Bの結果を眺めて、"都合のいいほう"を採用します(しがちです or する人もいます or ...)。 つまり、癌と正常組織が二群に分かれるのではないだろうかと事前に期待したことが、無意識(or意識的)に癌と正常がはっきりと二群に分かれる正規化法を探す行動に向かわせ、 結果として二群にはっきりと分かれた結果が得られた、という現実をつくる 自己成就予言(self-fulfilling prophecy)に(私を含め)ほとんどの人がなっているのだろうと思います。 これがいいことか悪いことかは...なんとも言えませんが、いずれにせよ正規化や前処理次第で結果が変わりうるという事実だけは知ってて損はないと思います。
解析 | クラスタリング | 階層的 | pvclust(Suzuki_2006)
最も一般的なクラスタリング手法。
このパッケージはさらに、二つのブートストラップ法により得られたクラスターのp値を表示してくれます。具体的には、 一般的なブートストラップ法によって得られるブートストラップ確率BP(Bootstrap Probability; 多数のサンプリングから特定のクラスターが形成される確率;樹形図上で緑色の数値)とともに、 より高精度なブートストラップ法であるmultiscale bootstrap resamplingにより得られた"近似的に偏りのない(Approximately Unbiased;樹形図上で赤色の数値)" 確率(%)を示してくれます。
(デフォルトでは)後者の方法により得られたp値が95%以上の確率で頑健なクラスターを四角く囲ってくれるところがこのパッケージの特徴です。
(今は解消されているのかもしれませんが、また私の理解が間違っているのかもしれませんが...)ブートストラップ回数を変えて結果を眺めると、 大元のクラスタリング結果は変わらずに枝に付加されるブートストラップ確率の値が微妙に変わるだけなはず(←この私の理解がまちがっていなければ)なのですが、"同じデータでも"樹形図の形が微妙に変わってしまうという経験をしました(ほかのユーザーからも同様のコメントをいただいたことがあります)。
2010/8/5にあらためて、例題のサンプルデータでリサンプリング回数を10,20,30回の場合でやってみると、ちゃんと樹形図の形が変わらずにブートストラップ確率の数値だけが変わっていたので、私からのバグレポートはできませんでした。どなたかこういう経験をなさったかたは下平先生(と私)までお願いいたします。
pvclustを行う際には
- 発現ベクトル間の類似度(method.dist): correlation (デフォルト; 1-相関係数に相当),uncentered, abscorなど
および
- クラスターをまとめる方法(method.hclust): average (デフォルト), single, complete, ward, mcquitty, median, centroid
を指定してやる必要があります。
数式などの詳細は参考PDFをごらんください。
また、ブートストラップ確率を計算するためのresampling回数も指定する必要があります。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し、以下をコピペ
1. 36 sample×22,283 genesからなるsample5.txtのサンプル間クラスタリングを行う場合:
in_f <- "sample5.txt" #入力ファイル名(発現データファイル)を指定してin_fに格納 param1 <- "correlation" #類似度(method.dist)を指定 param2 <- "average" #方法(method.hclust)を指定 param3 <- 20 #resampling回数を指定(この値が大きいほどより正確にブートストラップ確率を求めることができる。実際には100とか500とか...) #入力ファイルの読み込みとラベル情報の作成 library(pvclust) #パッケージの読み込み #データファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み out <- pvclust(data, method.hclust=param2, method.dist=param1, nboot=param3)#クラスタリングの実行 plot(out) #樹形図(デンドログラム)の表示 #以下は(こんなこともできますという)おまけ #Approximately Unbiased (au) probability > 0.95を満たす頑健なクラスターを四角で囲み、その条件を満たすクラスターのメンバーをリストアップしたい場合: param4 <- "au" #ブートストラップ確率計算手段を指定 param5 <- 0.95 #ブートストラップ確率の閾値を指定 pvrect(out, alpha=param5, pv=param4) #条件を満たすクラスターを四角で囲む pvpick(out, alpha=param5, pv=param4) #条件を満たすクラスターのメンバーをリストアップする
2. 10 sample×45 genesからなるsample3.txtのサンプル間クラスタリングを特に何も考えずデフォルト設定(resampling回数が1000となるのですごく時間がかかります...)で行う場合:
in_f <- "sample3.txt" #入力ファイル名(発現データファイル)を指定してin_fに格納 #必要なパッケージをロード library(pvclust) #パッケージの読み込み #データファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 out <- pvclust(data) #クラスタリングの実行plot(out)#樹形図(デンドログラム)の表示
3. 10 sample×45 genesからなるsample3.txtの遺伝子間クラスタリングをやる場合(pvclustでの遺伝子間クラスタリングは時間がかかりすぎるのでお勧めできません...):
in_f <- "sample3.txt" #入力ファイル名(発現データファイル)を指定してin_fに格納 param1 <- "correlation" #類似度(method.dist)を指定 param2 <- "average" #方法(method.hclust)を指定 param3 <- 30 #resampling回数を指定(この値が大きいほどより正確にブートストラップ確率を求めることができる。実際には100とか500とか...) #必要なパッケージをロード library(pvclust) #パッケージの読み込み #データファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 out <- pvclust(t(data), method.hclust=param2, method.dist=param1, nboot=param3)#クラスタリングの実行 plot(out) #樹形図(デンドログラム)の表示
解析 | クラスタリング | 階層的 | hclust
階層的クラスタリングのやり方を示します。1.用いた前処理法(MAS5やRMAなど)、2.スケーリング方法(対数変換やZ-scoreなど)、 3.距離(または非類似度)を定義する方法(ユークリッド距離など)、4.クラスターをまとめる方法(平均連結法やウォード法など)でどの方法を採用するかで結果が変わってきます。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し、以下をコピペ
1. サンプルデータ3のsample3.txtの場合:
サンプル間クラスタリング(距離:1-Pearson相関係数、方法:平均連結法(average))でR Graphics画面上に表示するやり方です。
in_f <- "sample3.txt" #入力ファイル名を指定してin_fに格納 param <- "average" #方法(method)を指定 #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 data.dist <- as.dist(1 - cor(data, method="pearson"))#サンプル間の距離を計算した結果をdata.distに格納 out <- hclust(data.dist, method=param) #階層的クラスタリングを実行した結果をoutに格納 plot(out) #樹形図(デンドログラム)の表示
2. サンプルデータ3のsample3.txtの場合:
サンプル間クラスタリング(距離:1-Pearson相関係数、方法:平均連結法(average))で図の大きさを指定してpng形式ファイルで保存するやり方です。
in_f <- "sample3.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge2.png" #出力ファイル名を指定してout_fに格納 param <- "average" #方法(method)を指定 param_fig <- c(500, 400) #ファイル出力時の横幅と縦幅を指定(単位はピクセル) #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 data.dist <- as.dist(1 - cor(data, method="pearson"))#サンプル間の距離を計算した結果をdata.distに格納 out <- hclust(data.dist, method=param) #階層的クラスタリングを実行した結果をoutに格納 #ファイルに保存 png(out_f, pointsize=13, width=param_fig[1], height=param_fig[2])#出力ファイルの各種パラメータを指定 plot(out) #樹形図(デンドログラム)の表示 dev.off() #おまじない
3. サンプルデータ3のsample3.txtの場合:
サンプル間クラスタリング(距離:1-Spearman相関係数、方法:平均連結法(average))で図の大きさを指定してpng形式ファイルで保存するやり方です。
in_f <- "sample3.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge3.png" #出力ファイル名を指定してout_fに格納 param <- "average" #方法(method)を指定 param_fig <- c(500, 400) #ファイル出力時の横幅と縦幅を指定(単位はピクセル) #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 data.dist <- as.dist(1 - cor(data, method="spearman"))#サンプル間の距離を計算した結果をdata.distに格納 out <- hclust(data.dist, method=param) #階層的クラスタリングを実行した結果をoutに格納 #ファイルに保存 png(out_f, pointsize=13, width=param_fig[1], height=param_fig[2])#出力ファイルの各種パラメータを指定 plot(out) #樹形図(デンドログラム)の表示 dev.off() #おまじない
4. サンプルデータ3のsample3.txtの場合:
サンプル間クラスタリング(距離:ユークリッド距離(euclidean)、方法:平均連結法(average))でR Graphics画面上に表示するやり方です。
in_f <- "sample3.txt" #入力ファイル名を指定してin_fに格納 param1 <- "euclidean" #距離(dist)を指定 param2 <- "average" #方法(method)を指定 #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 data.dist <- dist(t(data), method=param1)#サンプル間の距離を計算した結果をdata.distに格納 out <- hclust(data.dist, method=param2)#階層的クラスタリングを実行した結果をoutに格納 plot(out) #樹形図(デンドログラム)の表示
5. サンプルデータ3のsample3.txtの場合:
サンプル間クラスタリング(距離:ユークリッド距離(euclidean)、方法:平均連結法(average))で図の大きさを指定してpng形式ファイルで保存するやり方です。
in_f <- "sample3.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge5.png" #出力ファイル名を指定してout_fに格納 param1 <- "euclidean" #距離(dist)を指定 param2 <- "average" #方法(method)を指定 param_fig <- c(500, 400) #ファイル出力時の横幅と縦幅を指定(単位はピクセル) #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 data.dist <- dist(t(data), method=param1)#サンプル間の距離を計算した結果をdata.distに格納 out <- hclust(data.dist, method=param2)#階層的クラスタリングを実行した結果をoutに格納 #ファイルに保存 png(out_f, pointsize=13, width=param_fig[1], height=param_fig[2])#出力ファイルの各種パラメータを指定 plot(out) #樹形図(デンドログラム)の表示 dev.off() #おまじない
6. サンプルデータ3のsample3.txtの場合:
遺伝子間クラスタリング(距離:ユークリッド距離(euclidean)、方法:平均連結法(average))でR Graphics画面上に表示するやり方です。
in_f <- "sample3.txt" #入力ファイル名を指定してin_fに格納 param1 <- "euclidean" #距離(dist)を指定 param2 <- "average" #方法(method)を指定 #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 data.dist <- dist(data, method=param1) #遺伝子間の距離を計算した結果をdata.distに格納 out <- hclust(data.dist, method=param2)#階層的クラスタリングを実行した結果をoutに格納 plot(out) #樹形図(デンドログラム)の表示
7. サンプルデータ3のsample3.txtの場合:
遺伝子間クラスタリング(距離:1 - Spearman相関係数、方法:平均連結法(average))でR Graphics画面上に表示するやり方です。
in_f <- "sample3.txt" #入力ファイル名を指定してin_fに格納 param <- "average" #方法(method)を指定 #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 data.dist <- as.dist(1 - cor(t(data), method="spearman")) #遺伝子間の距離を計算した結果をdata.distに格納 out <- hclust(data.dist, method=param) #階層的クラスタリングを実行した結果をoutに格納 plot(out) #樹形図(デンドログラム)の表示
解析 | クラスタリング | 階層的 | hclust後の詳細な解析
解析 | クラスタリング | 階層的 | hclustで得られる情報は樹形図(デンドログラム)だけです。サンプル間クラスタリング程度なら得られる樹形図を眺めていろいろ考察することはできるでしょうが、数万遺伝子の遺伝子間クラスタリング結果だと不可能ですので、特に遺伝子間クラスタリング結果の詳細な解析を行いたい場合(もちろんサンプル間クラスタリング結果の詳細な解析にも利用可能です)にここで紹介するやり方を利用します。
ここでは、1. 「102 sample×3,274 genes」からなるdata_Singh_RMA_3274.txtや2. 「10 sample×45 genes」からなるsample3.txtの遺伝子間クラスタリングを行った後、任意のK個のクラスターに分割した場合にどの遺伝子(or サンプル)がどのクラスターに属するかを知るやり方を紹介します。当然のことながら、Kの最大値は1. の遺伝子間クラスタリングの結果だと3,274で、2.の遺伝子間クラスタリングの結果だと45となります。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し、以下をコピペ
1. data_Singh_RMA_3274.txtの遺伝子間クラスタリングの場合(類似度:1 - 相関係数、方法:平均連結法(average)):
in_f <- "data_Singh_RMA_3274.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge.txt" #出力ファイル名を指定してout_fに格納 param1 <- 10 #K個のクラスターに分割のKを指定 param2 <- "average" #方法(method)を指定 #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #まずはクラスタリングを実行 data.dist <- as.dist(1 - cor(t(data))) #遺伝子間の距離を計算し、結果をdata.distに格納 out <- hclust(data.dist, method=param2)#階層的クラスタリングを実行し、結果をoutに格納 #param1で指定した数に分割 cluster <- cutree(out, k=param1) #param1個のクラスターに分割し、結果をclusterに格納 #ファイルに保存 tmp <- cbind(rownames(data), data, cluster)#入力データの右側にclusterの情報を追加してtmpに格納。 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存 #以下は(こんなこともできますという)おまけ #クラスターごとにソートした結果を得たい場合: out_f2 <- "hoge2.txt" #出力ファイル名を指定してout_f2に格納 tmp2 <- tmp[order(cluster),] #cluster列の値でソートした結果をtmp2に格納 write.table(tmp2, out_f2, sep="\t", append=F, quote=F, row.names=F)#tmp2の中身を指定したファイル名で保存
2. sample3.txt遺伝子間クラスタリングの場合(類似度:ユークリッド距離(euclidean)、方法:平均連結法(average)):
in_f <- "sample3.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge.txt" #出力ファイル名を指定してout_fに格納 param1 <- 3 #K個のクラスターに分割のKを指定 param2 <- "euclidean" #距離(dist)を指定 param3 <- "average" #方法(method)を指定 #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #まずはクラスタリングを実行 data.dist <- dist(data, method=param2) #遺伝子間の距離を計算し、結果をdata.distに格納 out <- hclust(data.dist, method=param3)#階層的クラスタリングを実行し、結果をoutに格納 #param1で指定した数に分割 cluster <- cutree(out, k=param1) #param1個のクラスターに分割し、結果をclusterに格納 #ファイルに保存 tmp <- cbind(rownames(data), data, cluster)#入力データの右側にclusterの情報を追加してtmpに格納。 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存 #以下は(こんなこともできますという)おまけ #クラスターごとにソートした結果を得たい場合: out_f2 <- "hoge2.txt" #出力ファイル名を指定してout_f2に格納 tmp2 <- tmp[order(cluster),] #cluster列の値でソートした結果をtmp2に格納 write.table(tmp2, out_f2, sep="\t", append=F, quote=F, row.names=F)#tmp2の中身を指定したファイル名で保存
3. data_GSE7623_rma.txtのサンプル間クラスタリングの場合(類似度:1 - 相関係数、方法:平均連結法(average)):
in_f <- "data_GSE7623_rma.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge.txt" #出力ファイル名を指定してout_fに格納 param1 <- 2:10 #K個のクラスターに分割のKを指定(ここでは2-10を一度に指定←こんなこともできます) param2 <- "average" #方法(method)を指定 #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み colnames(data) <- c( #サンプル名を変更している "BAT_fed1", "BAT_fed2", "BAT_fed3", "BAT_fed4", #サンプル名を変更している "BAT_fasted1", "BAT_fasted2", "BAT_fasted3", "BAT_fasted4", #サンプル名を変更している "WAT_fed1", "WAT_fed2", "WAT_fed3", "WAT_fed4", #サンプル名を変更している "WAT_fasted1", "WAT_fasted2", "WAT_fasted3", "WAT_fasted4", #サンプル名を変更している "LIV_fed1", "LIV_fed2", "LIV_fed3", "LIV_fed4", #サンプル名を変更している "LIV_fasted1", "LIV_fasted2", "LIV_fasted3", "LIV_fasted4")#サンプル名を変更している #まずはクラスタリングを実行 data.dist <- as.dist(1 - cor(data)) #遺伝子間の距離を計算し、結果をdata.distに格納 out <- hclust(data.dist, method=param2)#階層的クラスタリングを実行し、結果をoutに格納 #param1で指定した数に分割 cluster <- cutree(out, k=param1) #param1個のクラスターに分割し、結果をclusterに格納 #ファイルに保存 tmp <- cbind(colnames(data), cluster) #サンプル名の右側にk個に分割した(例ではk=2,3,...,10)場合のclusterの情報を追加してtmpに格納。 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
解析 | クラスタリング | 階層的 | 最適なクラスター数を見積る
参考文献1の方法を用いてクラスター数を見積ります。
もしご自身のデータを実行したときに「メモリが足りない!」などと文句を言われたら、前処理 | フィルタリング | CVが小さいものを除去を参考にして遺伝子数を減らしてから行ってください。
以下では、前処理 | フィルタリング | CVが小さいものを除去の例題を実行して得られたAffymetrix Rat Genome 230 2.0 Arrayの対数変換後(log2変換後)の24 samples×2,127遺伝子からなる遺伝子発現データ(data_GSE7623_rma_cv.txt; 参考文献2)のサンプル間クラスタリングにおいて、最適なクラスター数kを見積り、各サンプルがどのクラスターに属しているかの結果を返すところまでを示します。
解析例で示す24 samples×2,127 genesからなる遺伝子発現行列データのサンプルラベル情報は以下の通りです。
GSM184414-184417: Brown adipose tissue (BAT), fed GSM184418-184421: Brown adipose tissue (BAT), 24 h-fasted GSM184422-184425: White adipose tissue (WAT), fed GSM184426-184429: White adipose tissue (WAT), 24 h-fasted GSM184430-184433: Liver tissue (LIV), fed GSM184434-184437: Liver tissue (LIV), 24 h-fasted
「ファイル」−「ディレクトリの変更」で解析したいファイル(data_GSE7623_rma_cv.txt)を置いてあるディレクトリに移動し、以下をコピペ
in_f <- "data_GSE7623_rma_cv.txt" #入力ファイル名を指定してin_fに格納 param1 <- 9 #クラスター数の探索範囲の上限 param2 <- "average" #方法(method)を指定 param3 <- 100 #ランダムサンプリング回数を指定(できれば1000くらいを指定したほうがよいと思います) #必要なパッケージをロード library(clusterStab) #パッケージの読み込み #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data <- as.matrix(data) #dataのデータ形式をmatrix型に変更 #本番 out <- benhur(data, 0.7, param1, seednum=12345, iterations=param3, linkmeth=param2)#最適クラスター数の探索を実行し、結果をoutに格納 hist(out) #候補クラスター数ごと(2, 3, ..., param)のJaccard係数分布を表示
解説:
ここでやっていることは、候補クラスター数k個について、2, 3, ..., param個の可能性について調べています。(間違っていたらすいません)
- まずはk=2の場合について調べます。
- もともとのサンプル数(この場合24サンプル)のデータについて階層的クラスタリングを行います。
- 得られた樹形図をもとにk個のクラスターに分けます。
- もともとのサンプル数のの70%のサンプル(subsamples)をランダムに抽出し階層的クラスタリングを行い、k個のクラスターに分けます。
- 3.のsubsamplesと4.のsubsamplesのクラスター間のJaccard係数?!を計算します。
- 4と5を"param3"回行い、Jaccard係数?!の分布を調べた結果がk=2のヒストグラムです。
- k=3, 4, ..., paramの場合についても同様の計算を行います。
したがって、Jaccard係数?!が1になった回数が"param3"回であれば一番理想的な結果となるわけです。
ですので、ヒストグラムの見方は、横軸のfrequencyが1.0のところに棒が集中、あるいはできるだけ1.0の近くにmajorityがあるようなヒストグラムを示すkの値が最適なクラスター数、という結論になります。解析例の場合はk=2 or 3が採用されるべきと判断します。
「以下にエラー plot.new() : 図の余白が大きす...」などとエラーメッセージが出る場合は、Rの画面を広げて、もう一度コマンドを実行してみてください。
ご自身のデータでヒストグラムの結果ではどのkを採用すればいいか判断がつきづらい場合には、以下をコピペしてみてください。これも見せ方を少し変えているだけで、解析例の場合だと、k=2がもっともよくて、二番目がk=5、三番目がk=6というような見方をします。
ecdf(out)
ここまでで、最適なクラスター数が2 or 3個であることがわかりました。次に参考文献3の方法を用いて各クラスターがどれだけ安定なのかをclusterComp関数を用いて調べるとともに、各サンプルがどのクラスターに属しているかの結果を指定した出力ファイル名で保存します。
param3 <- 2 #得られた最適なクラスター数(例では2)を指定 out_f <- "hoge.txt" #出力ファイル名を指定してout_fに格納 out2 <- clusterComp(data, param3, method=param2)#各クラスターの安定性を見積る out2 #out2の中身を表示(cluster1,2ともに100%の安定性であることが分かる) str(out2) #out2というオブジェクトの内容を情報付きで表示 out2@clusters #各サンプルがどのクラスターに属するのかを表示 #ファイルに保存 tmp <- cbind(names(out2@clusters), out2@clusters)#サンプル名とクラスター番号との対応関係をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
解析 | クラスタリング | 非階層的 | について
とりあえず枠組みのみ。
R用:
R以外:
- FCM(プログラムは提供していないようだ):Kim et al., BMC Bioinformatics, 2006
Review、ガイドライン、パイプライン系:
解析 | クラスタリング | 非階層的 | K-means
何個のクラスター(Kの数)にするのがよいか?(cluster validity問題)を探すために提案された指標(選択可)を用いて適切なクラスター数を計算する機能もついている。
「ファイル」−「ディレクトリの変更」で解析したいファイル(sample3.txt)を置いてあるディレクトリに移動。
in_f <- "sample3.txt" #入力ファイル名を指定してin_fに格納 #必要なパッケージをロード library(cclust) #パッケージの読み込み #データファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data <- as.matrix(data) #dataのデータ形式をmatrix型に変更 #まずはKをいろいろ変えて得られるクラスターを眺める sample3_k2 <- cclust(data, 2, 20, verbose=TRUE, method="kmeans")#K=2として遺伝子のクラスタリングを実行 sample3_k3 <- cclust(data, 3, 20, verbose=TRUE, method="kmeans")#K=3として遺伝子のクラスタリングを実行 sample3_k4 <- cclust(data, 4, 20, verbose=TRUE, method="kmeans")#K=4として遺伝子のクラスタリングを実行 sample3_k5 <- cclust(data, 5, 20, verbose=TRUE, method="kmeans")#K=5として遺伝子のクラスタリングを実行 sample3_k2 sample3_k3 sample3_k4 sample3_k5 #Cluster validity Indexの一つであるDB(Davies-Bouldin) Indexを用いて、K=2, 3, 4, 5として得られたクラスターを評価する clustIndex(sample3_k2, data, index="db") clustIndex(sample3_k3, data, index="db") clustIndex(sample3_k4, data, index="db") clustIndex(sample3_k5, data, index="db") #K=3でクラスタリングした結果(sample3_k3)から詳細な情報を入手したい場合。(2005.6.6追加) names(sample3_k3) #sample3_k3からどのような情報を入手できるのか調べる。 sample3_k3$cluster #遺伝子の並び順に、どのクラスに属するかをざっと表示 for(i in 1:nrow(sample3)) cat(rownames(data[i,])," ",sample3_k3$cluster[i],"\n")#遺伝子の並び順に、どの遺伝子がどのクラスに属するか全体を表示
DB Indexは、その値が低いものほど分割数が妥当であることを意味する。したがって、いろいろ調べた中で最も値の低かったものを採用(この場合、おそらくK=3)する。
(特にK=5とした場合に、Sizes of Clustersが1になるクラスターがときどき出現する。このような場合clustIndexで調べたときにエラーとなるようだ)
解析 | クラスタリング | 非階層的 | Self-Organizing Maps (SOM)
マイクロアレイデータ解析で似た発現パターンを示す遺伝子(or 組織)を自己組織化マップ(Self-Organizing Map; SOM)によりクラスタリングしたいときに用います。
「ファイル」−「ディレクトリの変更」で解析したい(sample2.txt)ファイルを置いてあるディレクトリに移動。
1. 組織(tissue)間クラスタリングの場合:
in_f <- "sample2.txt" #入力ファイル名を指定してin_fに格納 #必要なパッケージをロード library(som) #パッケージの読み込み #データファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #フィルタリング sample2.f <- filtering(data, lt=10, ut=100, mmr=2.9, mmd=42)#解析に用いる遺伝子のフィルタリング(発現強度が10以下のものを10に、100以上のものを100に、「発現強度max/min < 2.9」または「(max-min) < 42」の行(遺伝子)を解析から除く) sample2.f.n <- normalize(sample2.f, byrow=TRUE)#行(row)方向の正規化(平均=0,分散=1); (列方向にしたいときはcolにする) #本番 foo <- som(t(sample2.f.n), xdim=3, ydim=5)#SOMの実行(「x軸方向3分割×y軸方向5分割」にする場合) plot(foo) #結果のプロット
2. 遺伝子(gene)間クラスタリングの場合:
in_f <- "sample2.txt" #入力ファイル名を指定してin_fに格納 #必要なパッケージをロード library(som) #パッケージの読み込み #データファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #フィルタリング sample2.f <- filtering(data, lt=10, ut=100, mmr=2.9, mmd=42)#解析に用いる遺伝子のフィルタリング(発現強度が10以下のものを10に、100以上のものを100に、「発現強度max/min < 2.9」または「(max-min) < 42」の行(遺伝子)を解析から除く) sample2.f.n <- normalize(sample2.f, byrow=TRUE)#行(row)方向の正規化(平均=0,分散=1); (列方向にしたいときはcolにする) #本番 foo <- som(sample2.f.n, xdim=3, ydim=5)#SOMの実行(「x軸方向3分割×y軸方向5分割」にする場合) plot(foo) #結果のプロット
解析 | クラスタリング | 非階層的 | 主成分分析(PCA)
主成分分析(principal components analysis; PCA)によりクラスタリングしたいときに用います。
「ファイル」−「ディレクトリの変更」で解析したい(sample3.txt)ファイルを置いてあるディレクトリに移動。
in_f <- "sample3.txt" #入力ファイル名を指定 #データファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#発現データを読み込んでdataに格納。 #本番 data.pca <- prcomp(t(data)) names(data.pca) plot(data.pca$sdev, type="h", main="PCA s.d.") data.pca.sample <- t(data) %*% data.pca$rotation[,1:2]#第一、二主成分を抽出 plot(data.pca.sample, main="PCA") #第一、二主成分を抽出した結果をプロット text(data.pca.sample, colnames(data), col = c(rep("red", 7), rep("black", 3)))#tissue1-7を赤、残りの3つの組織を黒で表示。
解析 | 発現変動 | 2群間 | 発現変動遺伝子の割合を調べる | OCplus(Ploner_2006)
OCplusパッケージを用いて調べる方法を示します。
発現変動遺伝子(Differentially Expressed Genes; DEGs)のランキング(検出)を行う際にFDRを計算することで上位の遺伝子ですらFDRが1に近いものだと、
「ああこのデータセット中には発現変動遺伝子はないのね...。」という判断がつきます。
が、そんな回りくどいことをせずとも、以下を実行することで「発現変動遺伝子でないもの(non-DEGs)の割合」が一意に返されます。よって、「1 - その割合」がDEGsの割合ということになるのでざっくりと知ることができるわけです。
以下では(遺伝子名の列を除く)最初の3列(X=3)がG1群、残りの3列(Y=3)がG2群からなる(すでに対数変換されている)遺伝子発現データファイル(sample14.txt)の2群間比較用データのnon-DEGsの割合を計算する一連の手順を示します。
最後に出力される二つの数値が目的のものです。この場合、約65%がnon-DEGsであることがわかります。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し、以下をコピペ
1. サンプルデータ中のsample14.txtの場合:
in_f <- "sample14.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 3 #G1群のサンプル数を指定 param_G2 <- 3 #G2群のサンプル数を指定 #必要なパッケージをロード library(OCplus) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #本番 out1 <- fdr1d(data, data.cl, verb=FALSE)#入力データ中の発現変動していない遺伝子(non-DEGs)の割合を調べた結果をout1に格納 out2 <- EOC(data, data.cl) #入力データ中の発現変動していない遺伝子(non-DEGs)の割合を調べた結果をout2に格納 p0(out1) #得られたout1の中から目的のnon-DEGsの割合の数値を表示 p0(out2) #得られたout2の中から目的のnon-DEGsの割合の数値を表示
解析 | 発現変動 | 2群間 | 対応なし |について
実験デザインが以下のような場合にこのカテゴリーに属す方法を適用します:
Aさんの正常サンプル Bさんの正常サンプル Cさんの正常サンプル Dさんの腫瘍サンプル Eさんの腫瘍サンプル Fさんの腫瘍サンプル Gさんの腫瘍サンプル
2015年11月にざっと枠組みだけ作りました。
R用:
- WAD(TCCパッケージ中でWAD関数として提供):Kadota et al., Algorithms Mol. Biol., 2008
R以外:
- PED(MATLAB):Vasiliu et al., PLoS One, 2015
Review、ガイドライン、パイプライン系:
以下は相当古い(2011年頃の記述)ので参考まで。
「マーカー遺伝子の検出」が第一目的の場合と「分類精度が高い遺伝子セットを得たい」のが第一目的の場合で用いる方法が違ってきます。もちろん、両者は完全には排他的ではなくかなり密接に関連してはいますが、それぞれの目的に応じた手法が提案されているので使い分けるほうがよろしいかと思います。
「マーカー遺伝子の検出」が第一目的の場合(filter method;発現強度とサンプルクラス間の統計的な相関に基づいて遺伝子を抽出するやり方):
最近はFold change系とt-statistic系の組み合わせが主流?!になってきていますが、サンプル数(全部で10サンプル程度?!)が比較的少ないときは前者がよくて、比較的多いサンプル数(30サンプルとか?!)の場合には後者がいいと2007年ごろまで思っていました。 また、どのpreprocessing algorithmsを用いてexpression summary scoreを求めたデータに対して適用するかによっても違ってきます。私の2008年の論文(WAD: Kadota et al., 2008)での結論(おすすめ)は以下の通りです:
- 「MASアルゴリズム」のときは「WAD」
- 「RMAアルゴリズム」のときは「昔ながらのFold Change」
- 「DFWアルゴリズム」のときはRank products」
このうちのどれがいいかは分かりませんが、WADはRMAやDFWアルゴリズムでもFold ChangeやRank productsと同程度の成績を保持している一方、Fold ChangeとRank ProductsはMASアルゴリズムのとの相性が非常に悪いので、全体的にはWADが優れているのではという印象です。 ちなみにt-statistics系の方法はWAD(Kadota et al., 2008)論文が出る前まではMASアルゴリズムとの相性のよさで存在意義がありましたが...。
WAD論文中にも書いていますが、「なぜ雨後のたけのこのように手法論文が沢山publishされるのか?!」と思っていましたが、これは手法のデータセット依存性がかなりあるからだと思います。つまり、手法論文中では「シミュレーションデータでうまくいって、"a (せいぜい few) real experimental datasets"でうまくいきました」ということで論文として成立するのですが、"(many) other real datasets"でうまくいく保証がないのです(ここがみそ!)。
WAD論文では、アレイのデバイスが同じ計36個のreal experimental datasetsに対して、既知の発現変動遺伝子をどれだけ上位にランキングできるかという評価基準(具体的にはAUC)で、全体的にいいのはどれか?を比較した結果の結論が上記の組み合わせ、ということです(2008/6/26追加)。
その後様々な他のpreprocessing algorithmsとの相性を調べてみました。我々の論文(Kadota et al., 2009)中で提案した推奨ガイドラインは、以下の通りです。(2009/4/24追加)
感度・特異度の高いpreprocessing algorithmsとgene ranking methodsの組合せ:
- 「MASアルゴリズム」のときは「WAD」
- 「multi-mgMOSアルゴリズム」のときは「WAD」
- 「RMAアルゴリズム」のときは「Rank products」
- 「VSNアルゴリズム」のときは「Rank products」
- 「GCRMAアルゴリズム」のときは「Rank products」
- 「MBEIアルゴリズム」のときは「Rank products」
- 「PLIERアルゴリズム」のときは「Rank products」
- 「FARMSアルゴリズム」のときは「Rank products」
- 「DFWアルゴリズム」のときは「Rank products」
再現性の高いpreprocessing algorithmsとgene ranking methodsの組合せ:
- 上記nine algorithmsのいずれの場合でも「WAD」
上記ガイドラインはAffymetrix GeneChipデータのみを対象としたものであり、Agilentなど他のメーカーで測定されたデータに対する評価結果はKadota and Shimizu, 2011で報告しています。評価用データセットはMAQCのもので、Affymetrix, Agilent, Applied Biosystems, Illumina, GE Healthcareの5つのプラットフォームのデータで行っています。 結論としては、どのプラットフォームでも「再現性が高いのはWAD、感度・特異度が高いのはWAD or Rank products」というものであり、上記ガイドラインはプラットフォーム非依存であるという傍証を報告しています。
「分類精度が高い遺伝子セットを得たい」が第一目的の場合(wrapper method;分類能力の高い遺伝子を抽出するやり方):
- (こちらは私の専門ではないのでまだ知識不足ですのであしからず...)現在このページで紹介しているのはRandom forest (Diaz-Uriarte_2007) だけですが、他にもRで提供されているもの以外でBaker and Kramerの方法などがあります。 後者の論文のタイトルを見ればよく分かりますが、ずばり「分類精度が最も高い遺伝子セット」に的を絞って抽出してくれます。
解析 | 発現変動 | 2群間 | 対応なし | RankProd 2.0 (Del Carratore_2017)
RankProd 2.0パッケージを用いるやり方を示します。 この原著論文(Del Carratore et al., 2017)中にも明記されていますが、 Rank productsの一番最初の論文(Breitling et al., FEBS Lett., 2004)とはもはや別物のようです。 そのため、「解析 | 発現変動 | 2群間 | 対応なし | Rank products (Breitling_2004)」 とは別の項目として新設しました。ぱっと見妥当な結果になっているのでここで示したやり方でよいのではと思っておりますが、もし「何かオカシイ」 結果に遭遇しましたらお知らせください。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し、以下をコピペ
1. サンプルデータのdata_rma_2_BAT.txtの場合:
RMA-preprocessed data (G1群:4 samples vs. G2群:4 samples)です。
in_f <- "data_rma_2_BAT.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge1.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 4 #G1群のサンプル数を指定 param_G2 <- 4 #G2群のサンプル数を指定 #必要なパッケージをロード library(RankProd) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(0, param_G1), rep(1, param_G2))#G1群を0、G2群を1としたベクトルdata.clを作成 #本番 out <- RankProducts(data, data.cl, logged=T, na.rm=F, plot=F, rand=123)#RankProductsの実行 stat_RP <- apply(out$RPs, 1, min) #総合RP統計量を計算(20090527追加) rank_RP <- as.matrix(rank(stat_RP, ties.method = "min"))#総合順位を計算(20090527追加) stat_fc <- -out$AveFC #総合log(FC)統計量を計算 rank_fc <- rank(-abs(stat_fc)) #総合log(FC)統計量の順位を計算 #ファイルに保存 colnames(out$pfp) <- c("FDR(G1 < G2)","FDR(G1 > G2)")#列名を付与 colnames(out$RPs) <- c("stat(G1 < G2)","stat(G1 > G2)")#列名を付与 colnames(out$RPrank) <- c("rank(G1 < G2)","rank(G1 > G2)")#列名を付与 colnames(stat_fc) <- "log2(G2/G1)" #列名を付与 tmp <- cbind(rownames(data), data, out$pfp, out$RPs, out$RPrank, stat_fc, rank_fc, stat_RP, rank_RP)#入力データの右側にFDR値, 各統計量, 各順位, 総合log(FC)統計量, その順位, 総合RP統計量, その順位の情報を付加したtmpを用意。 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
解析 | 発現変動 | 2群間 | 対応なし | WAD (Kadota_2008)
Weighted Average Difference (WAD)法を用いて発現変動の度合いでランキング。
「既知発現変動遺伝子のほとんどは平均シグナル強度が高い」という事実に着目して、「一般的なlog ratioの値に対して(log scaleでの)、平均シグナル強度が高い遺伝子ほど1に近い重みをかけることで、上位にランキングされるようにしたもの」がWAD統計量です。
注意点としては、入力データはlog2-scaleのものを前提としているので、例えばRMAやDFWの出力結果ファイルはそのままWADの入力として用いていいですが、対数変換されていないデータファイルの場合は前処理 | スケーリング | シグナル強度を対数(log)変換するを参考にしてlog2変換したものに対してWADを適用してください。
以下Aug 2 2011追加。
WADに対してよく寄せられる質問として、「FDR計算できないんですけど...やWAD統計量ランキングしたときにどこまでを有意だと判断すればいいんでしょうか?」があります。
私が調べた限りでは、確かにFDRを計算できませんし、WAD統計量の閾値をどこに設定すればいいかはわかりません。これは事実です。
この原因としては、WAD統計量によるランキング結果の再現性が非常に高い、という特徴に起因しています。
つまり、例えば2群間(G1群vs.G2群)比較で、AやBのラベル情報をランダムに入れ替えてFDRを計算しようとしても、ランキング結果の再現性が高いが故に「random permutationで得られた結果は、元のランキング結果とほとんど同じランキング結果になってしまう」からです。
従って、何らかの客観的な閾値が欲しい、という人はSAMなり他の方法で「だいたいFDR < 0.05を満たす遺伝子数はこのくらい」という情報を別に持っておけばいいと思います。
実際問題としては、例えば(t統計量系の方法である)SAMで決めた任意の閾値を満たす遺伝子数やランキング結果と、
それ以外の(Fold change系の方法である)Rank productsで決めた同じ閾値を満たす遺伝子数やランキング結果は結構違います。
ランキング結果の上位x個という風に数を揃えても20%程度の一致しかないのが普通です。
では何を信じればいいのでしょうか?私は発現変動の度合いでランキングをした結果の上位に”本物”がより濃縮されている方法がいいと思います。
しかもそれが様々なプラットフォームや様々な評価基準でも有用性が示されているとしたら、、、WADでいいんじゃないかと思います。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し、以下をコピペ
1. 入力ファイルが既にlog2-transformed dataの場合(サンプルデータのdata_Singh_RMA_3274.txt):
以下では(遺伝子名の列を除く)最初の50列(X=50)が正常サンプル(G1群)、残りの52列(Y=52)が腫瘍サンプル(G2群)からなる
(すでに対数変換されている)遺伝子発現データファイル(data_Singh_RMA_3274.txt)の2群間比較を例とします。
in_f <- "data_Singh_RMA_3274.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge1.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 50 #G1群のサンプル数を指定 param_G2 <- 52 #G2群のサンプル数を指定 #WAD統計量を計算するための関数を定義 WAD <- function(data=NULL, data.cl=NULL){#WAD統計量を計算するための関数 x <- data #WAD統計量を計算するための関数 cl <- data.cl #WAD統計量を計算するための関数 mean1 <- rowMeans(as.matrix(x[, cl==1]))#WAD統計量を計算するための関数 mean2 <- rowMeans(as.matrix(x[, cl==2]))#WAD統計量を計算するための関数 x_ave <- (mean1 + mean2)/2 #WAD統計量を計算するための関数 weight <- (x_ave - min(x_ave))/(max(x_ave) - min(x_ave))#WAD統計量を計算するための関数 statistic <- (mean2 - mean1)*weight#WAD統計量を計算するための関数 return(statistic) #WAD統計量を計算するための関数 } #WAD統計量を計算するための関数 #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #本番 stat_wad <- WAD(data=data, data.cl=data.cl)#WADを実行し、WAD統計量を計算した結果をstat_wadに格納 rank_wad <- rank(-abs(stat_wad)) #WAD統計量の順位を計算した結果をrank_wadに格納 #ファイルに保存 tmp <- cbind(rownames(data), data, stat_wad, rank_wad)#入力データの右側に、「WAD統計量」と「その順位」を結合した結果をtmpに格納。 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
2. 入力ファイルがlogged dataでない場合(sample2.txt):
(遺伝子名の列を除く)最初の6列がG1群、残りの5列がG2群からなる(まだ対数変換されていない) 発現データです。
in_f <- "sample2.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge2.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 6 #G1群のサンプル数を指定 param_G2 <- 5 #G2群のサンプル数を指定 #WAD統計量を計算するための関数を定義 WAD <- function(data=NULL, data.cl=NULL){#WAD統計量を計算するための関数 x <- data #WAD統計量を計算するための関数 cl <- data.cl #WAD統計量を計算するための関数 mean1 <- rowMeans(as.matrix(x[, cl==1]))#WAD統計量を計算するための関数 mean2 <- rowMeans(as.matrix(x[, cl==2]))#WAD統計量を計算するための関数 x_ave <- (mean1 + mean2)/2 #WAD統計量を計算するための関数 weight <- (x_ave - min(x_ave))/(max(x_ave) - min(x_ave))#WAD統計量を計算するための関数 statistic <- (mean2 - mean1)*weight#WAD統計量を計算するための関数 return(statistic) #WAD統計量を計算するための関数 } #WAD統計量を計算するための関数 #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #発現データのシグナル強度が1未満のものを1にした後にlog2変換 data[data < 1] <- 1 #1未満のシグナル強度のものを1とする data <- log(data, 2) #log2スケーリング #本番 stat_wad <- WAD(data=data, data.cl=data.cl)#WADを実行し、WAD統計量を計算した結果をstat_wadに格納 rank_wad <- rank(-abs(stat_wad)) #WAD統計量の順位を計算した結果をrank_wadに格納 #ファイルに保存 tmp <- cbind(rownames(data), data, stat_wad, rank_wad)#入力データの右側に、「WAD統計量」と「その順位」を結合した結果をtmpに格納。 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
3. 入力ファイルがlogged dataでない場合(sample2.txt):
(遺伝子名の列を除く)最初の6列がG1群、残りの5列がG2群からなる(まだ対数変換されていない) 発現データです。TCCパッケージ中のWAD関数を用いるやり方です。 出力ファイル中のwad列がWAD統計量、rank列が発現変動順にソートした順位情報です。 WAD法はlog2変換後のデータを入力とすることを前提としており、発現レベルに相当する数値が1未満のものを1に変換してからlogをとっています。
in_f <- "sample2.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge3.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 6 #G1群のサンプル数を指定 param_G2 <- 5 #G2群のサンプル数を指定 #必要なパッケージをロード library(TCC) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #本番 out <- WAD(data, data.cl, logged=F, floor=1)#WADを実行した結果をoutに格納 #ファイルに保存 tmp <- cbind(rownames(data), data, out)#入力データの右側にDEG検出結果を結合したものをtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
解析 | 発現変動 | 2群間 | 対応なし | Random forest (Diaz-Uriarte_2007)
決定木の一種。日本語では「ランダム森 or ランダムフォレスト」というらしく、分類性能が非常に高いそうです。
以下では(遺伝子名の列を除く)最初の50列(X=50)が正常サンプル(G1群)、残りの52列(Y=52)が腫瘍サンプル(G2群)からなる(すでに対数変換されている)遺伝子発現データファイル(data_Singh_RMA_3274.txt)の2群間比較を例とします。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し、以下をコピペ
1. サンプルデータのdata_Singh_RMA_3274.txt(log2-transformed data)の場合:
in_f <- "data_Singh_RMA_3274.txt" #入力ファイル名を指定してin_fに格納 param_G1 <- 50 #G1群のサンプル数を指定 param_G2 <- 52 #G2群のサンプル数を指定 #必要なパッケージをロード library(varSelRF) #varSelRFパッケージの読み込み #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #本番 rf.vs1 <- varSelRF(t(data), factor(data.cl))#RFをデフォルトのパラメータを用いて実行 rf.vs1$selected.vars #最終的に選ばれた遺伝子を表示
解析 | 発現変動 | 2群間 | 対応なし | shrinkage t (Opgen-Rhein_2007)
参考文献1の方法(Distribution-Free Shrinkage Approach)を用いて2群間で発現の異なる遺伝子をランキング。 このライブラリ中では、他に参考文献2の方法(t statistic using the 90% rule of Efron et al., 2001)、 empirical Bayes (Smyth_2004)、SAM(Tusher_2001)の計算もやってくれるので、ここでは全部の結果を出力します。
以下では(遺伝子名の列を除く)最初の50列(X=50)が正常サンプル(G1群)、残りの52列(Y=52)が腫瘍サンプル(G2群)からなる(すでに対数変換されている)遺伝子発現データファイル(data_Singh_RMA_3274.txt)の2群間比較を例とします。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し、以下をコピペ
1. サンプルデータのdata_Singh_RMA_3274.txt(log2-transformed data)の場合:
in_f <- "data_Singh_RMA_3274.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 50 #G1群のサンプル数を指定 param_G2 <- 52 #G2群のサンプル数を指定 #必要なパッケージをロード library(st) #shrinkage t statisticを計算するためのパッケージの読み込み library(samr) #SAMを計算するためのパッケージの読み込み library(limma) #empirical Bayesを計算するためのパッケージの読み込み #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #本番 stat_st <- shrinkt.stat(t(data), data.cl)#Shrinkage t統計量を計算し結果をstat_stに格納 rank_st <- rank(-abs(stat_st)) #Shrinkage t統計量の順位を計算し結果をrankt_stに格納 stat_efron <- efront.stat(t(data), data.cl)#Efron's t統計量を計算し結果をstat_efronに格納 rank_efron <- rank(-abs(stat_efron)) #Efron's t統計量の順位を計算し結果をrank_efronに格納 stat_ebayes <- modt.stat(t(data), data.cl)#Empirical Bayes t統計量を計算し結果をstat_ebayesに格納 rank_ebayes <- rank(-abs(stat_ebayes)) #Empirical Bayes t統計量の順位を計算し結果をrank_ebayesに格納 stat_sam <- sam.stat(t(data), data.cl) #SAM's t統計量を計算し結果をstat_samに格納 rank_sam <- rank(-abs(stat_sam)) #SAM's t統計量の順位を計算し結果をrank_samに格納 #ファイルに保存 tmp <- cbind(rownames(data), data, stat_st, rank_st, stat_efron, rank_efron, stat_ebayes, rank_ebayes, stat_sam, rank_sam)#「それぞれの計算方法で得られた統計量」と「その順位」をShrinkage, Efron, empirical Bayes, SAMの順に右のカラムに結合した結果をtmpに格納。 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
解析 | 発現変動 | 2群間 | 対応なし | layer ranking algorithm (Chen_2007)
参考文献1の方法を用いて2群間で発現の異なる遺伝子をランキング。この論文中では三つのlayer ranking algorithms (point-admissible, line-admissible, and Pareto)を提案しています。
MicroArray Quality Control (MAQC)プロジェクトではより再現性の高い発現変動遺伝子セットを抽出するために
「倍率変化(Fold change)によるランキング;Fold-change ranking」と「緩めのp-valueカットオフ;non-stringent p-value cutoff」の両方を用いることをお勧めしています(参考文献2)。
これは最近よく使われる候補遺伝子抽出のための手続きであり、前者(log ratio)を横軸、後者(-log(p-value, base=10)など)を縦軸として得られる図を"volcano plot"といいます。しかしこれでは候補遺伝子セットが得られるだけで、その2つのランキングから得られる総合ランキングをどうやって得るかが問題です。
参考文献1でChenらは「複数の候補遺伝子ランキング法→総合ランキング」を得るための三つの方法を提案しています。
一つめはpoint-admissible layer ranking (method="rlfq"で指定), 二つめはline-admissible layer ranking (method="convex"で指定), そして三つめはPareto layer ranking (method="pareto"で指定)です。ここでは、一つの解析例を挙げておきます。
以下では(遺伝子名の列を除く)最初の50列(X=50)が正常サンプル(G1群)、残りの52列(Y=52)が腫瘍サンプル(G2群)からなる(すでに対数変換されている)遺伝子発現データファイル(data_Singh_RMA_3274.txt)の2群間比較用データを用いて、
- 「log2(幾何平均版のFold change)の絶対値でのランキング」と「SAM統計量の絶対値でのランキング」→ Pareto layer ranking (method="pareto"で指定)で総合ランキング
- 「log2(幾何平均版のFold change)の絶対値でのランキング」と「Welch t統計量の絶対値でのランキング」→ Pareto layer ranking (method="pareto"で指定)で総合ランキング
- 「log2(算術平均版のFold change)の絶対値でのランキング」と「Welch t統計量の絶対値でのランキング」→ Pareto layer ranking (method="pareto"で指定)で総合ランキング
を得るやり方を示します。
コピペで動かないままになっていたのを修正しました(2009/11/10, 12:38)。
「ファイル」−「ディレクトリの変更」で解析したいサンプルデータのdata_Singh_RMA_3274.txtファイルを置いてあるディレクトリに移動し、以下をコピペ
1. 「log2(幾何平均版のFold change)の絶対値でのランキング」と「SAM統計量の絶対値でのランキング」の場合:
in_f <- "data_Singh_RMA_3274.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 50 #G1群のサンプル数を指定 param_G2 <- 52 #G2群のサンプル数を指定 param3 <- "pareto" #ランキング法を指定 #必要なパッケージなどをロード #source("http://gap.stat.sinica.edu.tw/Software/mvo.R")#layer ranking algorithmのRスクリプトの読み込み source("http://www.iu.a.u-tokyo.ac.jp/~kadota/R/mvo.R")#layer ranking algorithmのRスクリプトの読み込み library(samr) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #本番 data.tmp = list(x=data, y=data.cl, geneid=rownames(data), genenames=rownames(data), logged2=TRUE)#SAMを実行するsamr関数の入力フォーマットに合わせたdata.tmpという入力データを作成 out <- samr(data.tmp, resp.type="Two class unpaired", nperms=20)#samr関数を実行し、結果をoutに格納 stat_sam <- out$tt #SAM統計量をstat_samに格納 rank_sam <- rank(-abs(stat_sam)) #SAM統計量の順位をrank_samに格納 stat_fc <- log2(out$foldchange) #log(FC)統計量をstat_fcに格納 rank_fc <- rank(-abs(stat_fc)) #log(FC)統計量の順位をrank_fcに格納 ranks <- cbind(stat_sam, stat_fc) #SAM統計量とFC統計量をまとめたものをranksに格納。 ranks.out <- mvo(ranks,ignore=c(T,T),opposite=c(F,F), empty=F, method=param3)#param3で指定した総合ランキングを実行 #ファイルに保存 tmp <- cbind(rownames(data), data, stat_sam, stat_fc, rank_sam, rank_fc, ranks.out)#入力データの右側に「SAM統計量」「log(FC)」「SAM統計量の順位」「log(FC)の順位」「layer ranking」情報を追加してtmpに格納。 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
以下の計算を実行すると(結構時間がかかります)一位に"37639_at"と"41468_at"の2つが、二位に"1740_g_at"と"37366_at"が、そして三位に"1890_at"など計三つがランキングされていることが分かります。(hoge.txtをエクセルのタブ区切りテキストで開くとFカラムからこれらの情報が分かります。)
ここではPareto layer ranking (method="pareto"で指定)で総合ランキングを得ているので、 同じ順位内の遺伝子群は「log2(Fold change)の絶対値でのランキング」または「SAMのd統計量の絶対値でのランキング」いずれかで、同じ順位内の他の遺伝子に対して勝っています。
例えば、総合ランキング三位の三つの遺伝子は、(総合ランキング一位と二位を除いて)"1890_at"は「log ratioの絶対値での順位」がトップ(4位)です。"32598_at"は「d統計量の絶対値での順位」がトップ(4位)。 "38827_at"はそれぞれのランキングはともに5位ですが、「log ratioの絶対値での順位」は"32598_at"に勝っており、「d統計量の絶対値での順位」は"1890_at"に勝っているので、順位的に劣っているとはみなさない、というのがここでのPareto layer rankingの考え方です。
2. 「log2(幾何平均版のFold change)の絶対値でのランキング」と「Welch t統計量の絶対値でのランキング」の場合:
in_f <- "data_Singh_RMA_3274.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 50 #G1群のサンプル数を指定 param_G2 <- 52 #G2群のサンプル数を指定 param3 <- "pareto" #ランキング法を指定 #必要な関数などをロード source("http://www.iu.a.u-tokyo.ac.jp/~kadota/R/mvo.R")#layer ranking algorithmのRスクリプトの読み込み source("http://www.iu.a.u-tokyo.ac.jp/~kadota/R/R_functions.R")#Welch t-testを行うWelch_ttest関数を含むファイルをあらかじめ読み込む #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #本番 out <- t(apply(data, 1, Welch_ttest, data.cl))#各(行)遺伝子についてt検定を行った結果のt統計量とp値をoutに格納 stat_t <- out[,1] #t統計量をstat_tに格納 rank_t <- rank(-abs(stat_t)) #t統計量の順位をrank_tに格納 stat_fc <- apply(data, 1, AD, data.cl) #log(FC)統計量(AD統計量)をstat_fcに格納 rank_fc <- rank(-abs(stat_fc)) #log(FC)統計量の順位をrank_fcに格納 ranks <- cbind(stat_t, stat_fc) #t統計量とFC統計量をまとめたものをranksに格納。 ranks.out <- mvo(ranks,ignore=c(T,T),opposite=c(F,F), empty=F, method=param3)#param3で指定した総合ランキングを実行 #ファイルに保存 tmp <- cbind(rownames(data), data, stat_t, stat_fc, rank_t, rank_fc, ranks.out)#入力データの右側に「t統計量」「log(FC)」「t統計量の順位」「log(FC)の順位」「layer ranking」情報を追加してtmpに格納。 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
3. 「log2(算術平均版のFold change)の絶対値でのランキング」と「Welch t統計量の絶対値でのランキング」の場合:
in_f <- "data_Singh_RMA_3274.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 50 #G1群のサンプル数を指定 param_G2 <- 52 #G2群のサンプル数を指定 param3 <- "pareto" #ランキング法を指定 #必要な関数などをロード source("http://www.iu.a.u-tokyo.ac.jp/~kadota/R/mvo.R")#layer ranking algorithmのRスクリプトの読み込み source("http://www.iu.a.u-tokyo.ac.jp/~kadota/R/R_functions.R")#Welch t-testを行うWelch_ttest関数を含むファイルをあらかじめ読み込む #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #本番 out <- t(apply(data, 1, Welch_ttest, data.cl))#各(行)遺伝子についてt検定を行った結果のt統計量とp値をoutに格納 stat_t <- out[,1] #t統計量をstat_tに格納 rank_t <- rank(-abs(stat_t)) #t統計量の順位をrank_tに格納 stat_fc <- apply(data, 1, FC, data.cl) #log(FC)統計量をstat_fcに格納 rank_fc <- rank(-abs(stat_fc)) #log(FC)統計量の順位をrank_fcに格納 ranks <- cbind(stat_t, stat_fc) #t統計量とFC統計量をまとめたものをranksに格納。 ranks.out <- mvo(ranks,ignore=c(T,T),opposite=c(F,F), empty=F, method=param3)#param3で指定した総合ランキングを実行 #ファイルに保存 tmp <- cbind(rownames(data), data, stat_t, stat_fc, rank_t, rank_fc, ranks.out)#入力データの右側に「t統計量」「log(FC)」「t統計量の順位」「log(FC)の順位」「layer ranking」情報を追加してtmpに格納。 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
解析 | 発現変動 | 2群間 | 対応なし | fdr2d (Ploner_2006)
一つ上のlayer ranking algorithm (Chen_2007)と同じく、発現変動遺伝子(Differentially Expressed Genes; DEGs)のランキングのために用いた複数の統計量(例えばFold changeとP-value)の結果から総合ランキングを得るとともにそのFDRを計算してくれるようです。
サンプルの並べ替え(permutation)でnon-DEGsの分布を計算し、どうにかしてFDRを計算してくれるみたいです。
以下では(遺伝子名の列を除く)最初の3列(X=3)がG1群、残りの3列(Y=3)がG2群からなる(すでに対数変換されている)遺伝子発現データファイル(sample14.txt)の2群間比較用データを用いて、
「標準誤差のlog」と「t統計量」で総合FDRを得るやり方を示します。
volcano plot (横軸:fold change, 縦軸:t-testなどで得られたp-value)の総合FDRは下記で利用しているfdr2d関数ではサポートされていないようですね。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し、以下をコピペ
1. サンプルデータのsample14.txtの場合:
in_f <- "sample14.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 3 #G1群のサンプル数を指定 param_G2 <- 3 #G2群のサンプル数を指定 #必要なパッケージをロード library(OCplus) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #本番 tmpout <- fdr1d(data, data.cl, verb=FALSE)#入力データ中の発現変動していない遺伝子(non-DEGs)の割合を調べた結果をtmpoutに格納 p0(tmpout) #得られたtmpoutの中から目的のnon-DEGsの割合の数値を表示 out <- fdr2d(data, data.cl, p0=p0(tmpout), verb=FALSE)#「標準誤差のlog」と「t統計量」の二つの統計量の値を使って総合FDRを計算 #ファイルに保存 tmp <- cbind(rownames(data), data, out)#入力データの右側に「t統計量(tstat)」「標準誤差のlog(logse)」「総合FDR」情報を追加してtmpに格納。 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
解析 | 発現変動 | 2群間 | 対応なし | IBMT (Sartor_2006)
IBMT法 (Sartor et al., 2006)の方法を用いて2群間で発現の異なる遺伝子をランキング。 empirical Bayes (Smyth_2004)の改良版という位置づけですね。a novel Bayesian moderated-Tと書いてますし。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し、以下をコピペ
1. サンプルデータ20の31,099 probesets×8 samplesのdata_rma_2_LIV.txt(G1群4サンプル vs. G2群4サンプル)の場合:
in_f <- "data_rma_2_LIV.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge1.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 4 #G1群のサンプル数を指定 param_G2 <- 4 #G2群のサンプル数を指定 #必要なパッケージなどをロード library(limma) #パッケージの読み込み source("http://eh3.uc.edu/r/ibmtR.R") #IBMTのRスクリプトの読み込み #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #本番 #design <- model.matrix(~ as.factor(data.cl))#デザイン行列を作成した結果をdesignに格納 design <- model.matrix(~data.cl) #デザイン行列を作成した結果をdesignに格納 fit <- lmFit(data, design) #モデル構築(ばらつきの程度を見積もっている) fit$Amean<-rowMeans(data) #おまじない fit <- IBMT(fit,2) #IBMTプログラムの実行 p.value <- fit$IBMT.p #p値をp.valueに格納 q.value <- p.adjust(p.value, method="BH")#q値をq.valueに格納 ranking <- rank(p.value) #p.valueでランキングした結果をrankingに格納 sum(q.value < 0.05) #FDR < 0.05を満たす遺伝子数を表示 #ファイルに保存 tmp <- cbind(rownames(data), data, p.value, q.value, ranking)#入力データの右側にp.value、q.value、rankingを結合した結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
2. サンプルデータ24の31,099 probesets×10 samplesのdata_GSE30533_rma.txt(G1群5サンプル vs. G2群5サンプル)の場合:
in_f <- "data_GSE30533_rma.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge2.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 5 #G1群のサンプル数を指定 param_G2 <- 5 #G2群のサンプル数を指定 #必要なパッケージをロード library(limma) #パッケージの読み込み source("http://eh3.uc.edu/r/ibmtR.R") #IBMTのRスクリプトの読み込み #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #本番 #design <- model.matrix(~ as.factor(data.cl))#デザイン行列を作成した結果をdesignに格納 design <- model.matrix(~data.cl) #デザイン行列を作成した結果をdesignに格納 fit <- lmFit(data, design) #モデル構築(ばらつきの程度を見積もっている) fit$Amean<-rowMeans(data) #おまじない fit <- IBMT(fit,2) #IBMTプログラムの実行 p.value <- fit$IBMT.p #p値をp.valueに格納 q.value <- p.adjust(p.value, method="BH")#q値をq.valueに格納 ranking <- rank(p.value) #p.valueでランキングした結果をrankingに格納 sum(q.value < 0.05) #FDR < 0.05を満たす遺伝子数を表示 #ファイルに保存 tmp <- cbind(rownames(data), data, p.value, q.value, ranking)#入力データの右側にp.value、q.value、rankingを結合した結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
解析 | 発現変動 | 2群間 | 対応なし | Rank products (Breitling_2004) 非推奨
「解析 | 発現変動 | 2群間 | 対応なし | RankProd 2.0 (Del Carratore_2017)」をご利用下さい!(2019年3月16日追加) Rank products法 (Breitling et al., 2004)を用いて2群間で発現の異なる遺伝子をランキング。 非常によく用いられているSAMよりも成績がいいとのこと。 実際、手法比較論文(Jeffery et al., BMC Bioinformatics, 2006)中でも高い評価を受けているようだ。 この方法を使って遺伝子のランキングをした結果はt検定やSAMなどとは"かなり"違います(Kadota et al., Algorithms Mol. Biol., 2008)。 出力ファイル中の「log/unlog(class1/class2)」列の名前を「log(G2/G1)」に変更しました。 G2/G1はG2群とG1群の平均発現レベルのfold change (FC)です。それゆえ、log(G2/G1)はいわゆる"log ratio"とか"log比"と呼ばれるものです。 その右側の「rank_fc」列は、このlog比の絶対値が大きい順にランキングした結果です。(2015/02/12追加)。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し、以下をコピペ
1. サンプルデータのdata_rma_2_BAT.txtの場合:
RMA-preprocessed data (G1群:4 samples vs. G2群:4 samples)です。
in_f <- "data_rma_2_BAT.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge1.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 4 #G1群のサンプル数を指定 param_G2 <- 4 #G2群のサンプル数を指定 param_perm <- 100 #並べ替え回数を指定(数値が大きいほどより正確だがその分だけ時間がかかる。実際の解析ではサンプル数にもよるが最低でも1000以上を推奨) #必要なパッケージをロード library(RankProd) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #本番 out <- RP(data, data.cl, num.perm = param_perm, logged = TRUE, na.rm = FALSE, plot = FALSE, rand = 123)#Rank Product (RP)の実行 stat_RP <- apply(out$RPs, 1, min) #総合RP統計量を計算(20090527追加) rank_RP <- as.matrix(rank(stat_RP, ties.method = "min"))#総合順位を計算(20090527追加) stat_fc <- -out$AveFC #総合log(FC)統計量を計算 rank_fc <- rank(-abs(stat_fc)) #総合log(FC)統計量の順位を計算 #ファイルに保存 colnames(out$pfp) <- c("FDR(G1 < G2)","FDR(G1 > G2)")#列名を付与 colnames(out$RPs) <- c("stat(G1 < G2)","stat(G1 > G2)")#列名を付与 colnames(out$RPrank) <- c("rank(G1 < G2)","rank(G1 > G2)")#列名を付与 colnames(stat_fc) <- "log2(G2/G1)" #列名を付与 tmp <- cbind(rownames(data), data, out$pfp, out$RPs, out$RPrank, stat_fc, rank_fc, stat_RP, rank_RP)#入力データの右側にFDR値, 各統計量, 各順位, 総合log(FC)統計量, その順位, 総合RP統計量, その順位の情報を付加したtmpを用意。 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
2. サンプルデータのdata_rma_2_BAT.txtの場合:
RMA-preprocessed data (G1群:4 samples vs. G2群:4 samples)でFDR < 0.05を満たすprobesetIDの情報のみ抽出するやり方です。 若干IDの数に変動はあると思いますが概ね1800 IDsが得られると思います。 result_rankprod_BAT_id.txtのような感じの結果が得られるはずです。
in_f <- "data_rma_2_BAT.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge2.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 4 #G1群のサンプル数を指定 param_G2 <- 4 #G2群のサンプル数を指定 param_perm <- 100 #並べ替え回数を指定(数値が大きいほどより正確だがその分だけ時間がかかる。実際の解析ではサンプル数にもよるが最低でも1000以上を推奨) param_FDR <- 0.05 #false discovery rate (FDR)閾値を指定 #必要なパッケージをロード library(RankProd) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #本番 out <- RP(data, data.cl, num.perm = param_perm, logged = TRUE, na.rm = FALSE, plot = FALSE, rand = 123)#Rank Product (RP)の実行。 hoge_upG2 <- rownames(data)[out$pfp[1] < param_FDR]#「G2群 > G1群」の中で指定したFDR閾値を満たすIDを抽出 hoge_upG1 <- rownames(data)[out$pfp[2] < param_FDR]#「G2群 < G1群」の中で指定したFDR閾値を満たすIDを抽出 tmp <- union(hoge_upG1, hoge_upG2) #(両方で共通して出現しているIDがごくまれにあるので念のため)和集合をとっている #ファイルに保存 writeLines(tmp, out_f) #tmpの中身を指定したファイル名で保存
3. サンプルデータのdata_Singh_RMA_3274.txt(log2-transformed data)の場合:
RMA-preprocessed data (G1群:50 samples vs. G2群:52 samples)です。
in_f <- "data_Singh_RMA_3274.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge3.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 50 #G1群のサンプル数を指定 param_G2 <- 52 #G2群のサンプル数を指定 param_perm <- 20 #並べ替え回数を指定(数値が大きいほどより正確だがその分だけ時間がかかる。実際の解析ではサンプル数にもよるが最低でも1000以上を推奨) #必要なパッケージをロード library(RankProd) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #本番 out <- RP(data, data.cl, num.perm = param_perm, logged = TRUE, na.rm = FALSE, plot = FALSE, rand = 123)#Rank Product (RP)の実行。 stat_RP <- apply(out$RPs, 1, min) #総合RP統計量を計算(20090527追加) rank_RP <- as.matrix(rank(stat_RP, ties.method = "min"))#総合順位を計算(20090527追加) stat_fc <- -out$AveFC #総合log(FC)統計量を計算 rank_fc <- rank(-abs(stat_fc)) #総合log(FC)統計量の順位を計算 #ファイルに保存 colnames(out$pfp) <- c("FDR(G1 < G2)","FDR(G1 > G2)")#列名を付与 colnames(out$RPs) <- c("stat(G1 < G2)","stat(G1 > G2)")#列名を付与 colnames(out$RPrank) <- c("rank(G1 < G2)","rank(G1 > G2)")#列名を付与 colnames(stat_fc) <- "log2(G2/G1)" #列名を付与 tmp <- cbind(rownames(data), data, out$pfp, out$RPs, out$RPrank, stat_fc, rank_fc, stat_RP, rank_RP)#入力データの右側にFDR値, 各統計量, 各順位, 総合log(FC)統計量, その順位, 総合RP統計量, その順位の情報を付加したtmpを用意。 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存 #以下は(こんなこともできますという)おまけ plotRP(out, cutoff = 0.05) #FDRを5%に設定したときのG2群(この場合Tumourサンプル)で高発現(2つの図の上)および低発現(2つの図の下)のdifferentially expressed genesが赤色で示される。この場合だとそれぞれ500個程度あることが分かる。 topGene(out, cutoff = 0.0001, gene.names = rownames(data))#FDR0.01%を満たす遺伝子をリストアップ。(いっぱいあることが分かります。)尚、オプションのgene.namesはrownames(data)とちゃんと指定してあげないと遺伝子名のところがシリアル番号?!(gene.indexカラムの数字と同じ)になってしまいます。 topGene(out, num.gene = 10, gene.names = rownames(data))#上位10遺伝子をリストアップしたいとき summary(out) #outからどのような情報を抽出できるか調べる。
得られるhoge3.txtについて。
- FDR列:pfp (percentage of false positive predictionの略;FDRそのもの)値。この列で昇順にソートして0.05未満のもののリストなどをゲットしたりする。
- stat列:RPs (RP or RPadvance関数を使ったときはrank product;RSadvance関数を使ったときはrank sum)値。統計量そのものです。低いほど発現変動の度合いが高いことを意味する。
- rank列:順位
- log(G2/G1)列:log比(G2の算術平均 - G1の算術平均)値。
- rank_fc列:stat_fc値の絶対値が大きい順に並べた順位。
- stat_RP列:二つある"stat"列の統計量のうち、小さいほうの値。この値が小さいほど発現変動の度合いが大きいと解釈する。
- rank_RP列:総合順位。Rank列は、「G1 < G2での順位」と「G1 > G2での順位」が独立に出てくるので、WADの順位との比較を行いたいなどの場合には、この総合順位を用いて行います。
解析 | 発現変動 | 2群間 | 対応なし | empirical Bayes (Smyth_2004)
limmaパッケージを用いて2群間比較を行うやり方を示します。 この方法は経験ベイズと表現されたり、moderated t statisticと表現されたりしているようです。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し、以下をコピペ
1. サンプルデータ20のdata_rma_2_LIV.txtの場合:
31,099 probesets×8 samples(G1群4サンプル vs. G2群4サンプル)のデータです。
in_f <- "data_rma_2_LIV.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge1.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 4 #G1群のサンプル数を指定 param_G2 <- 4 #G2群のサンプル数を指定 #必要なパッケージをロード library(limma) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #本番 #design <- model.matrix(~ as.factor(data.cl))#デザイン行列を作成した結果をdesignに格納 design <- model.matrix(~data.cl) #デザイン行列を作成した結果をdesignに格納 fit <- lmFit(data, design) #モデル構築(ばらつきの程度を見積もっている) out <- eBayes(fit) #検定(経験ベイズ) p.value <- out$p.value[,ncol(design)] #p値をp.valueに格納 q.value <- p.adjust(p.value, method="BH")#q値をq.valueに格納 ranking <- rank(p.value) #p.valueでランキングした結果をrankingに格納 sum(q.value < 0.05) #FDR < 0.05を満たす遺伝子数を表示 #ファイルに保存 tmp <- cbind(rownames(data), data, p.value, q.value, ranking)#入力データの右側にDEG検出結果を結合したものをtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
2. サンプルデータ24のdata_GSE30533_rma.txtの場合:
31,099 probesets×10 samples(G1群5サンプル vs. G2群5サンプル)のデータです。
in_f <- "data_GSE30533_rma.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge2.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 5 #G1群のサンプル数を指定 param_G2 <- 5 #G2群のサンプル数を指定 #必要なパッケージをロード library(limma) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #本番 #design <- model.matrix(~ as.factor(data.cl))#デザイン行列を作成した結果をdesignに格納 design <- model.matrix(~data.cl) #デザイン行列を作成した結果をdesignに格納 fit <- lmFit(data, design) #モデル構築(ばらつきの程度を見積もっている) out <- eBayes(fit) #検定(経験ベイズ) p.value <- out$p.value[,ncol(design)] #p値をp.valueに格納 q.value <- p.adjust(p.value, method="BH")#q値をq.valueに格納 ranking <- rank(p.value) #p.valueでランキングした結果をrankingに格納 sum(q.value < 0.05) #FDR < 0.05を満たす遺伝子数を表示 #ファイルに保存 tmp <- cbind(rownames(data), data, p.value, q.value, ranking)#入力データの右側にDEG検出結果を結合したものをtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
3. サンプルデータ20のdata_rma_2_LIV.txtの場合:
31,099 probesets×8 samples(G1群4サンプル vs. G2群4サンプル)のデータです。M-A plotのpngファイルを生成しています。
in_f <- "data_rma_2_LIV.txt" #入力ファイル名を指定してin_fに格納 out_f1 <- "hoge3.txt" #出力ファイル名を指定してout_f1に格納 out_f2 <- "hoge3.png" #出力ファイル名を指定してout_f2に格納 param_G1 <- 4 #G1群のサンプル数を指定 param_G2 <- 4 #G2群のサンプル数を指定 param_FDR <- 0.05 #false discovery rate (FDR)閾値を指定 param_fig <- c(400, 380) #ファイル出力時の横幅と縦幅を指定(単位はピクセル) #必要なパッケージをロード library(limma) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #本番 #design <- model.matrix(~ as.factor(data.cl))#デザイン行列を作成した結果をdesignに格納 design <- model.matrix(~data.cl) #デザイン行列を作成した結果をdesignに格納 fit <- lmFit(data, design) #モデル構築(ばらつきの程度を見積もっている) out <- eBayes(fit) #検定(経験ベイズ) p.value <- out$p.value[,ncol(design)] #p値をp.valueに格納 q.value <- p.adjust(p.value, method="BH")#q値をq.valueに格納 ranking <- rank(p.value) #p.valueでランキングした結果をrankingに格納 sum(q.value < 0.05) #FDR < 0.05を満たす遺伝子数を表示 #ファイルに保存(テキストファイル) tmp <- cbind(rownames(data), data, p.value, q.value, ranking)#入力データの右側にDEG検出結果を結合したものをtmpに格納 write.table(tmp, out_f1, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存 #ファイルに保存(M-A plot) mean_G1 <- apply(as.matrix(data[,data.cl==1]), 1, mean)#遺伝子ごとにG1群の平均を計算した結果をmean_G1に格納 mean_G2 <- apply(as.matrix(data[,data.cl==2]), 1, mean)#遺伝子ごとにG2群の平均を計算した結果をmean_G2に格納 M <- mean_G2 - mean_G1 #M-A plotのM値(y軸の値)に相当するものをMに格納 A <- (mean_G1 + mean_G2)/2 #M-A plotのA値(x軸の値)に相当するものをAに格納 png(out_f2, pointsize=13, width=param_fig[1], height=param_fig[2])#出力ファイルの各種パラメータを指定 plot(A, M, xlab="A = (G2 + G1)/2", ylab="M = G2 - G1", cex=.1, pch=20)#M-A plotを描画 grid(col="gray", lty="dotted") #指定したパラメータでグリッドを表示 obj <- as.logical(q.value < param_FDR) #条件を満たすかどうかを判定した結果をobjに格納(DEGがTRUE、non-DEGがFALSE) points(A[obj], M[obj], col="magenta", cex=0.1, pch=20)#objがTRUEとなる要素のみ指定した色で描画 legend("topright", c(paste("DEG(FDR<", param_FDR, ")", sep=""), "non-DEG"),#凡例を作成している col=c("magenta", "black"), pch=20)#凡例を作成している dev.off() #おまじない
4. サンプルデータ20のdata_rma_2_LIV.txtの場合:
31,099 probesets×8 samples(G1群4サンプル vs. G2群4サンプル)のデータです。 M-A plotのpngファイルを生成しています。limmaパッケージ中のplotMA関数を用いるやり方です。
in_f <- "data_rma_2_LIV.txt" #入力ファイル名を指定してin_fに格納 out_f1 <- "hoge4.txt" #出力ファイル名を指定してout_f1に格納 out_f2 <- "hoge4.png" #出力ファイル名を指定してout_f2に格納 param_G1 <- 4 #G1群のサンプル数を指定 param_G2 <- 4 #G2群のサンプル数を指定 param_FDR <- 0.05 #false discovery rate (FDR)閾値を指定 param_fig <- c(400, 380) #ファイル出力時の横幅と縦幅を指定(単位はピクセル) #必要なパッケージをロード library(limma) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #本番 #design <- model.matrix(~ as.factor(data.cl))#デザイン行列を作成した結果をdesignに格納 design <- model.matrix(~data.cl) #デザイン行列を作成した結果をdesignに格納 fit <- lmFit(data, design) #モデル構築(ばらつきの程度を見積もっている) out <- eBayes(fit) #検定(経験ベイズ) p.value <- out$p.value[,ncol(design)] #p値をp.valueに格納 q.value <- p.adjust(p.value, method="BH")#q値をq.valueに格納 ranking <- rank(p.value) #p.valueでランキングした結果をrankingに格納 sum(q.value < 0.05) #FDR < 0.05を満たす遺伝子数を表示 #ファイルに保存(テキストファイル) tmp <- cbind(rownames(data), data, p.value, q.value, ranking)#入力データの右側にDEG検出結果を結合したものをtmpに格納 write.table(tmp, out_f1, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存 #ファイルに保存(M-A plot) png(out_f2, pointsize=13, width=param_fig[1], height=param_fig[2])#出力ファイルの各種パラメータを指定 plotMA(fit, cex=0.1, pch=20) #M-A plotを描画 grid(col="gray", lty="dotted") #指定したパラメータでグリッドを表示 obj <- as.logical(q.value < param_FDR) #条件を満たすかどうかを判定した結果をobjに格納 points(fit$Amean[obj], fit$coef[obj,ncol(design)], col="magenta", cex=0.1, pch=20)#objがTRUEとなる要素のみ指定した色で描画 legend("topright", c(paste("DEG(FDR<", param_FDR, ")", sep=""), "non-DEG"),#凡例を作成している col=c("magenta", "black"), pch=20)#凡例を作成している dev.off() #おまじない
5. サンプルデータ20のdata_rma_2_LIV.txtの場合:
31,099 probesets×8 samples(G1群4サンプル vs. G2群4サンプル)のデータです。 M-A plotのpngファイルを生成しています。シリーズ Useful R 第7巻 トランスクリプトーム解析のp170のコードに似せた記述形式です。
in_f <- "data_rma_2_LIV.txt" #入力ファイル名を指定してin_fに格納 out_f1 <- "hoge5.txt" #出力ファイル名を指定してout_f1に格納 out_f2 <- "hoge5.png" #出力ファイル名を指定してout_f2に格納 param_G1 <- 4 #G1群のサンプル数を指定 param_G2 <- 4 #G2群のサンプル数を指定 param_FDR <- 0.05 #false discovery rate (FDR)閾値を指定 param_fig <- c(400, 380) #ファイル出力時の横幅と縦幅を指定(単位はピクセル) #必要なパッケージをロード library(limma) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #本番 #design <- model.matrix(~ as.factor(data.cl))#デザイン行列を作成した結果をdesignに格納 design <- model.matrix(~data.cl) #デザイン行列を作成した結果をdesignに格納 fit <- lmFit(data, design) #モデル構築(ばらつきの程度を見積もっている) out <- eBayes(fit) #検定(経験ベイズ) p.value <- out$p.value[,ncol(design)] #p値をp.valueに格納 q.value <- p.adjust(p.value, method="BH")#q値をq.valueに格納 ranking <- rank(p.value) #p.valueでランキングした結果をrankingに格納 sum(q.value < 0.05) #FDR < 0.05を満たす遺伝子数を表示 #ファイルに保存(テキストファイル) tmp <- cbind(rownames(data), data, p.value, q.value, ranking)#入力データの右側にDEG検出結果を結合したものをtmpに格納 write.table(tmp, out_f1, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存 #ファイルに保存(M-A plot) hoge <- topTable(out,coef=colnames(design)[ncol(design)], adjust="BH",number= nrow(data))#発現変動順にソートした結果をhogeに格納 M <- hoge$logFC #M-A plotのM値(y軸の値)に相当するものをMに格納 A <- hoge$AveExpr #M-A plotのA値(x軸の値)に相当するものをAに格納 png(out_f2, pointsize=13, width=param_fig[1], height=param_fig[2])#出力ファイルの各種パラメータを指定 plot(A, M, xlab="AveExpr", ylab="logFC", cex=.1, pch=20)#M-A plotを描画 grid(col="gray", lty="dotted") #指定したパラメータでグリッドを表示 obj <- as.logical(hoge$adj.P.Val < param_FDR) #条件を満たすかどうかを判定した結果をobjに格納 points(A[obj], M[obj], col="magenta", cex=0.1, pch=20)#objがTRUEとなる要素のみ指定した色で描画 legend("topright", c(paste("DEG(FDR<", param_FDR, ")", sep=""), "non-DEG"),#凡例を作成している col=c("magenta", "black"), pch=20)#凡例を作成している dev.off() #おまじない
6. サンプルデータ20のdata_rma_2_LIV.txtの場合:
31,099 probesets×8 samples(G1群4サンプル vs. G2群4サンプル)のデータです。 M-A plotのpngファイルを生成しています。シリーズ Useful R 第7巻 トランスクリプトーム解析 のp170のコードに似せた記述形式です。テキストファイルのほうの出力結果をtopTable関数の出力結果にしています。
in_f <- "data_rma_2_LIV.txt" #入力ファイル名を指定してin_fに格納 out_f1 <- "hoge6.txt" #出力ファイル名を指定してout_f1に格納 out_f2 <- "hoge6.png" #出力ファイル名を指定してout_f2に格納 param_G1 <- 4 #G1群のサンプル数を指定 param_G2 <- 4 #G2群のサンプル数を指定 param_FDR <- 0.05 #false discovery rate (FDR)閾値を指定 param_fig <- c(400, 380) #ファイル出力時の横幅と縦幅を指定(単位はピクセル) #必要なパッケージをロード library(limma) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #本番 #design <- model.matrix(~ as.factor(data.cl))#デザイン行列を作成した結果をdesignに格納 design <- model.matrix(~data.cl) #デザイン行列を作成した結果をdesignに格納 fit <- lmFit(data, design) #モデル構築(ばらつきの程度を見積もっている) out <- eBayes(fit) #検定(経験ベイズ) hoge <- topTable(out,coef=colnames(design)[ncol(design)], adjust="BH",number= nrow(data))#発現変動順にソートした結果をhogeに格納 sum(hoge$adj.P.Val < 0.05) #FDR < 0.05を満たす遺伝子数を表示 #ファイルに保存(テキストファイル) tmp <- cbind(rownames(hoge), data[rownames(hoge),], hoge)#入力データの右側にDEG検出結果を結合したものをtmpに格納 write.table(tmp, out_f1, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存 #ファイルに保存(M-A plot) M <- hoge$logFC #M-A plotのM値(y軸の値)に相当するものをMに格納 A <- hoge$AveExpr #M-A plotのA値(x軸の値)に相当するものをAに格納 png(out_f2, pointsize=13, width=param_fig[1], height=param_fig[2])#出力ファイルの各種パラメータを指定 plot(A, M, xlab="AveExpr", ylab="logFC", cex=.1, pch=20)#M-A plotを描画 grid(col="gray", lty="dotted") #指定したパラメータでグリッドを表示 obj <- as.logical(hoge$adj.P.Val < param_FDR) #条件を満たすかどうかを判定した結果をobjに格納 points(A[obj], M[obj], col="magenta", cex=0.1, pch=20)#objがTRUEとなる要素のみ指定した色で描画 legend("topright", c(paste("DEG(FDR<", param_FDR, ")", sep=""), "non-DEG"),#凡例を作成している col=c("magenta", "black"), pch=20)#凡例を作成している dev.off() #おまじない
7. サンプルデータ20のdata_rma_2_LIV.txtの場合:
31,099 probesets×8 samples(G1群4サンプル vs. G2群4サンプル)のデータです。 M-A plotのpngファイルを生成しています。limmaパッケージ中のtopTable関数やplotMA関数を使わないやり方です。 テキストファイルのほうは、M-A plotのM値とA値も出力させるようにしています。
in_f <- "data_rma_2_LIV.txt" #入力ファイル名を指定してin_fに格納 out_f1 <- "hoge7.txt" #出力ファイル名を指定してout_f1に格納 out_f2 <- "hoge7.png" #出力ファイル名を指定してout_f2に格納 param_G1 <- 4 #G1群のサンプル数を指定 param_G2 <- 4 #G2群のサンプル数を指定 param_FDR <- 0.05 #false discovery rate (FDR)閾値を指定 param_fig <- c(400, 380) #ファイル出力時の横幅と縦幅を指定(単位はピクセル) #必要なパッケージをロード library(limma) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #本番 #design <- model.matrix(~ as.factor(data.cl))#デザイン行列を作成した結果をdesignに格納 design <- model.matrix(~data.cl) #デザイン行列を作成した結果をdesignに格納 fit <- lmFit(data, design) #モデル構築(ばらつきの程度を見積もっている) out <- eBayes(fit) #検定(経験ベイズ) p.value <- out$p.value[,ncol(design)] #p値をp.valueに格納 q.value <- p.adjust(p.value, method="BH")#q値をq.valueに格納 ranking <- rank(p.value) #p.valueでランキングした結果をrankingに格納 sum(q.value < 0.05) #FDR < 0.05を満たす遺伝子数を表示 mean_G1 <- apply(as.matrix(data[,data.cl==1]), 1, mean)#遺伝子ごとにG1群の平均を計算した結果をmean_G1に格納 mean_G2 <- apply(as.matrix(data[,data.cl==2]), 1, mean)#遺伝子ごとにG2群の平均を計算した結果をmean_G2に格納 M <- mean_G2 - mean_G1 #M-A plotのM値(y軸の値)に相当するものをMに格納 A <- (mean_G1 + mean_G2)/2 #M-A plotのA値(x軸の値)に相当するものをAに格納 #ファイルに保存(テキストファイル) tmp <- cbind(rownames(data), data, M, A, p.value, q.value, ranking)#入力データの右側にDEG検出結果を結合したものをtmpに格納 write.table(tmp, out_f1, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存 #ファイルに保存(M-A plot) png(out_f2, pointsize=13, width=param_fig[1], height=param_fig[2])#出力ファイルの各種パラメータを指定 plot(A, M, xlab="A = (G2 + G1)/2", ylab="M = G2 - G1", cex=.1, pch=20)#M-A plotを描画 grid(col="gray", lty="dotted") #指定したパラメータでグリッドを表示 obj <- as.logical(q.value < param_FDR) #条件を満たすかどうかを判定した結果をobjに格納(DEGがTRUE、non-DEGがFALSE) points(A[obj], M[obj], col="magenta", cex=0.1, pch=20)#objがTRUEとなる要素のみ指定した色で描画 legend("topright", c(paste("DEG(FDR<", param_FDR, ")", sep=""), "non-DEG"),#凡例を作成している col=c("magenta", "black"), pch=20)#凡例を作成している dev.off() #おまじない
8. サンプルデータ20のdata_rma_2_LIV.txtの場合:
31,099 probesets×8 samples(G1群4サンプル vs. G2群4サンプル)のデータです。 M-A plotのpngファイルを生成しています。limmaパッケージ中のtopTable関数やplotMA関数を使わないやり方です。 7.を基本としつつ、テキストファイルのほうは発現変動順にソートしたものを出力しています。 また、param_FCで指定した倍率変化に相当するM-A plot上のMの閾値を水平線で引いています。
in_f <- "data_rma_2_LIV.txt" #入力ファイル名を指定してin_fに格納 out_f1 <- "hoge8.txt" #出力ファイル名を指定してout_f1に格納 out_f2 <- "hoge8.png" #出力ファイル名を指定してout_f2に格納 param_G1 <- 4 #G1群のサンプル数を指定 param_G2 <- 4 #G2群のサンプル数を指定 param_FDR <- 0.05 #false discovery rate (FDR)閾値を指定 param_FC <- 2 #倍率変化の閾値を指定 param_fig <- c(400, 380) #ファイル出力時の横幅と縦幅を指定(単位はピクセル) #必要なパッケージをロード library(limma) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #本番 #design <- model.matrix(~ as.factor(data.cl))#デザイン行列を作成した結果をdesignに格納 design <- model.matrix(~data.cl) #デザイン行列を作成した結果をdesignに格納 fit <- lmFit(data, design) #モデル構築(ばらつきの程度を見積もっている) out <- eBayes(fit) #検定(経験ベイズ) p.value <- out$p.value[,ncol(design)] #p値をp.valueに格納 q.value <- p.adjust(p.value, method="BH")#q値をq.valueに格納 ranking <- rank(p.value) #p.valueでランキングした結果をrankingに格納 sum(q.value < 0.05) #FDR < 0.05を満たす遺伝子数を表示 mean_G1 <- apply(as.matrix(data[,data.cl==1]), 1, mean)#遺伝子ごとにG1群の平均を計算した結果をmean_G1に格納 mean_G2 <- apply(as.matrix(data[,data.cl==2]), 1, mean)#遺伝子ごとにG2群の平均を計算した結果をmean_G2に格納 M <- mean_G2 - mean_G1 #M-A plotのM値(y軸の値)に相当するものをMに格納 A <- (mean_G1 + mean_G2)/2 #M-A plotのA値(x軸の値)に相当するものをAに格納 #ファイルに保存(テキストファイル) tmp <- cbind(rownames(data), data, M, A, p.value, q.value, ranking)#入力データの右側にDEG検出結果を結合したものをtmpに格納 tmp <- tmp[order(ranking),] #rankingでソートした結果をtmpに格納 write.table(tmp, out_f1, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存 #ファイルに保存(M-A plot) png(out_f2, pointsize=13, width=param_fig[1], height=param_fig[2])#出力ファイルの各種パラメータを指定 plot(A, M, xlab="A = (G2 + G1)/2", ylab="M = G2 - G1", cex=.1, pch=20)#M-A plotを描画 grid(col="gray", lty="dotted") #指定したパラメータでグリッドを表示 obj <- as.logical(q.value < param_FDR) #条件を満たすかどうかを判定した結果をobjに格納(DEGがTRUE、non-DEGがFALSE) points(A[obj], M[obj], col="magenta", cex=0.1, pch=20)#objがTRUEとなる要素のみ指定した色で描画 legend("topright", c(paste("DEG(FDR<", param_FDR, ")", sep=""), "non-DEG"),#凡例を作成している col=c("magenta", "black"), pch=20)#凡例を作成している abline(h=log2(param_FC), col="red") #M=log2(param_FC)の直線を表示 abline(h=-log2(param_FC), col="red") #M=-log2(param_FC)の直線を表示 dev.off() #おまじない
解析 | 発現変動 | 2群間 | 対応なし | samroc (Broberg_2003)
参考文献1の方法を用いて2群間で発現の異なる遺伝子をランキング。ROC curveに基づいてSAM統計量を計算したもの。 よく用いられているSAMよりも成績がいいとのこと(Choe et al., Genome Biol., 2005)。
余談ですが、samroc著者のBrobergさんは発現変動遺伝子(DEG)でないものnon-DEG (or nonDEG)の割合を見積もる方法についての論文も出してます(Broberg P, BMC Bioinformatics, 2005)。
出力ファイルの「p.value」列がp値、「ranking」列がp値に基づく順位、「q.value」列が任意のFDR閾値を満たすものを調べるときに用いるものです。 実用上はq.value = FDRという理解で差し支えありません。例えば、「FDR < 0.05」を満たすものはq.valueが0.05未満のものに相当します。 p値を閾値とする際には有意水準5%などというという用語を用いますが、事実上「p < 0.05」などという表現を用いるのと同じです。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し、以下をコピペ
1. サンプルデータ20の31,099 probesets×8 samplesのdata_rma_2_LIV.txt(G1群4サンプル vs. G2群4サンプル)の場合:
in_f <- "data_rma_2_LIV.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge1.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 4 #G1群のサンプル数を指定 param_G2 <- 4 #G2群のサンプル数を指定 param1 <- 2000 #ブートストラップリサンプリング回数(defaultの100だと結果がころころ変わるので多めにしています) #必要なパッケージをロード library(SAGx) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #本番 out <- samrocNboot(data=data, formula=~as.factor(data.cl), B=param1)#samrocを実行 show(out) #結果を表示 p.value <- out@pvalues #p値をp.valueに格納 q.value <- p.adjust(p.value, method="BH")#q値をq.valueに格納 ranking <- rank(p.value) #p.valueでランキングした結果をrankingに格納 #ファイルに保存 tmp <- cbind(rownames(data), data, p.value, q.value, ranking)#入力データの右側にp.value、q.value、rankingを結合した結果をtmpに格納。 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
2. サンプルデータ24の31,099 probesets×10 samplesのdata_GSE30533_rma.txt(G1群5サンプル vs. G2群5サンプル)の場合:
in_f <- "data_GSE30533_rma.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge2.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 50 #G1群のサンプル数を指定 param_G2 <- 52 #G2群のサンプル数を指定 param1 <- 2000 #ブートストラップリサンプリング回数(defaultの100だと結果がころころ変わるので多めにしています) #必要なパッケージをロード library(SAGx) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #本番 out <- samrocNboot(data=data, formula=~as.factor(data.cl), B=param1)#samrocを実行 show(out) #結果を表示 p.value <- out@pvalues #p値をp.valueに格納 q.value <- p.adjust(p.value, method="BH")#q値をq.valueに格納 ranking <- rank(p.value) #p.valueでランキングした結果をrankingに格納 #ファイルに保存 tmp <- cbind(rownames(data), data, p.value, q.value, ranking)#入力データの右側にp.value、q.value、rankingを結合した結果をtmpに格納。 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
解析 | 発現変動 | 2群間 | 対応なし | SAM
Significance Analysis of Microarrays (SAM)法。改良版t-statisticを用いて発現強度依存の偏りを補正すべく、従来のt-statisticの数式の分母に補正項(fudge factor)を付加しているところがポイント。
ここでは、「SAM統計量とその順位」および「log(FC)統計量とその順位」を出力結果として得るやり方を示します。また、入力データは対数変換後のものを想定(logged2=TRUE)しています。
出力ファイルの「p.value」列がp値、「ranking」列がp値に基づく順位、「q.value」列が任意のFDR閾値を満たすものを調べるときに用いるものです。 実用上はq.value = FDRという理解で差し支えありません。例えば、「FDR < 0.05」を満たすものはq.valueが0.05未満のものに相当します。 p値を閾値とする際には有意水準5%などというという用語を用いますが、事実上「p < 0.05」などという表現を用いるのと同じです。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し、以下をコピペ
1. サンプルデータ20の31,099 probesets×8 samplesのdata_rma_2_LIV.txt(G1群4サンプル vs. G2群4サンプル)の場合:
in_f <- "data_rma_2_LIV.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge1.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 4 #G1群のサンプル数を指定 param_G2 <- 4 #G2群のサンプル数を指定 param_perm <- 100 #並べ替え回数を指定(数値が大きいほどより正確だがその分だけ時間がかかる。実際の解析ではサンプル数にもよるが最低でも1000以上を推奨) #必要なパッケージをロード library(samr) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #本番 data.tmp <- list(x=as.matrix(data), #SAMを実行するsamr関数の入力フォーマットに合わせたdata.tmpを作成 y=data.cl, #SAMを実行するsamr関数の入力フォーマットに合わせたdata.tmpを作成 geneid=rownames(data), #SAMを実行するsamr関数の入力フォーマットに合わせたdata.tmpを作成 genenames=rownames(data),#SAMを実行するsamr関数の入力フォーマットに合わせたdata.tmpを作成 logged2=TRUE) #SAMを実行するsamr関数の入力フォーマットに合わせたdata.tmpを作成 out <- samr(data.tmp, resp.type="Two class unpaired", nperms=param_perm)#samr関数を実行し、結果をoutに格納。 summary(out) #outからどのような情報が抜き出せるか調べる。 p.value <- samr.pvalues.from.perms(out$tt, out$ttstar)#p値をp.valueに格納 q.value <- p.adjust(p.value, method="BH")#q値をq.valueに格納 ranking <- rank(p.value) #p.valueでランキングした結果をrankingに格納 stat_fc <- log2(out$foldchange) #log(FC)統計量をstat_fcに格納 rank_fc <- rank(-abs(stat_fc)) #統計量の絶対値でランキングした結果をrank_fcに格納 #ファイルに保存 tmp <- cbind(rownames(data), data, p.value, q.value, ranking, stat_fc, rank_fc)#入力データの右側にp.value、q.value、ranking、log(G2/G1)、log(G2/G1)の順位を結合した結果をtmpに格納。 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
2. サンプルデータ24の31,099 probesets×10 samplesのdata_GSE30533_rma.txt(G1群5サンプル vs. G2群5サンプル)の場合:
in_f <- "data_GSE30533_rma.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge2.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 50 #G1群のサンプル数を指定 param_G2 <- 52 #G2群のサンプル数を指定 param_perm <- 20 #並べ替え回数を指定(数値が大きいほどより正確だがその分だけ時間がかかる。実際の解析ではサンプル数にもよるが最低でも1000以上を推奨) #必要なパッケージをロード library(samr) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #本番 data.tmp <- list(x=as.matrix(data), #SAMを実行するsamr関数の入力フォーマットに合わせたdata.tmpを作成 y=data.cl, #SAMを実行するsamr関数の入力フォーマットに合わせたdata.tmpを作成 geneid=rownames(data), #SAMを実行するsamr関数の入力フォーマットに合わせたdata.tmpを作成 genenames=rownames(data),#SAMを実行するsamr関数の入力フォーマットに合わせたdata.tmpを作成 logged2=TRUE) #SAMを実行するsamr関数の入力フォーマットに合わせたdata.tmpを作成 out <- samr(data.tmp, resp.type="Two class unpaired", nperms=param_perm)#samr関数を実行し、結果をoutに格納。 summary(out) #outからどのような情報が抜き出せるか調べる。 p.value <- samr.pvalues.from.perms(out$tt, out$ttstar)#p値をp.valueに格納 q.value <- p.adjust(p.value, method="BH")#q値をq.valueに格納 ranking <- rank(p.value) #p.valueでランキングした結果をrankingに格納 stat_fc <- log2(out$foldchange) #log(FC)統計量をstat_fcに格納 rank_fc <- rank(-abs(stat_fc)) #統計量の絶対値でランキングした結果をrank_fcに格納 #ファイルに保存 tmp <- cbind(rownames(data), data, p.value, q.value, ranking, stat_fc, rank_fc)#入力データの右側にp.value、q.value、ranking、log(G2/G1)、log(G2/G1)の順位を結合した結果をtmpに格納。 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
解析 | 発現変動 | 2群間 | 対応なし | Student's t-test
等分散性を仮定したt検定を用いて、2群間での発現変動遺伝子の同定を行うやり方を示します。
出力ファイルの「p.value」列がp値、「ranking」列がp値に基づく順位、「q.value」列が任意のFDR閾値を満たすものを調べるときに用いるものです。 実用上はq.value = FDRという理解で差し支えありません。例えば、「FDR < 0.05」を満たすものはq.valueが0.05未満のものに相当します。 p値を閾値とする際には有意水準5%などというという用語を用いますが、事実上「p < 0.05」などという表現を用いるのと同じです。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し、以下をコピペ
1. サンプルデータ16のsample16_log.txt(対数変換後のデータ)の場合:
クラスラベル情報ファイル(sample16_cl.txt)を利用するやり方です。
in_f1 <- "sample16_log.txt" #入力ファイル名を指定してin_f1に格納(発現データ) in_f2 <- "sample16_cl.txt" #入力ファイル名を指定してin_f2に格納(テンプレート情報) out_f <- "hoge1.txt" #出力ファイル名を指定してout_fに格納 #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f1, header=TRUE, row.names=1, sep="\t", quote="")#in_f1で指定したファイルの読み込み hoge <- read.table(in_f2, sep="\t", quote="")#in_f2で指定したファイルの読み込み data.cl <- hoge[,2] + 1 #テンプレートパターンベクトルhoge[,2]は0 or 1であるが、このウェブページではグループラベル情報を1 or 2で取り扱っているので、そうなるように全部に1を足した結果をdata.clに格納 #等分散性を仮定(var.equal=T)してt.testを行い、t統計量とp-valueの値を返す関数Students_ttestを作成。 Students_ttest <- function(x, cl){ x.class1 <- x[(cl == 1)] #ラベルが1のものをx.class1に格納 x.class2 <- x[(cl == 2)] #ラベルが2のものをx.class2に格納 if((sd(x.class1)+sd(x.class2)) == 0){#両方の群の標準偏差が共に0の場合は計算できないので... stat <- 0 #統計量を0 pval <- 1 #p値を1 return(c(stat, pval)) #として結果を返す } else{ #G1, G2どちらかの群の標準偏差が0(上記条件以外)の場合は hoge <- t.test(x.class1, x.class2, var.equal=T)#通常のt検定を行って、 return(c(hoge$statistic, hoge$p.value))#統計量とp値を結果として返す } } #本番 out <- t(apply(data, 1, Students_ttest, data.cl))#各(行)遺伝子についてt検定を行った結果のt統計量とp値をoutに格納 p.value <- out[,2] #p値をp.valueに格納 q.value <- p.adjust(p.value, method="BH")#q値をq.valueに格納 ranking <- rank(p.value) #p.valueでランキングした結果をrankingに格納 #ファイルに保存 tmp <- cbind(rownames(data), data, p.value, q.value, ranking)#入力データの右側にp.value、q.value、rankingを結合した結果をtmpに格納。 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
2. サンプルデータ16のsample16_log.txt(対数変換後のデータ)の場合:
クラスラベル情報ファイル(sample16_cl.txt)を利用しないやり方です。
in_f <- "sample16_log.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge2.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 6 #G1群のサンプル数を指定 param_G2 <- 5 #G2群のサンプル数を指定 #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #等分散性を仮定(var.equal=T)してt.testを行い、t統計量とp-valueの値を返す関数Students_ttestを作成。 Students_ttest <- function(x, cl){ x.class1 <- x[(cl == 1)] #ラベルが1のものをx.class1に格納 x.class2 <- x[(cl == 2)] #ラベルが2のものをx.class2に格納 if((sd(x.class1)+sd(x.class2)) == 0){#両方の群の標準偏差が共に0の場合は計算できないので... stat <- 0 #統計量を0 pval <- 1 #p値を1 return(c(stat, pval)) #として結果を返す } else{ #G1, G2どちらかの群の標準偏差が0(上記条件以外)の場合は hoge <- t.test(x.class1, x.class2, var.equal=T)#通常のt検定を行って、 return(c(hoge$statistic, hoge$p.value))#統計量とp値を結果として返す } } #本番 out <- t(apply(data, 1, Students_ttest, data.cl))#各(行)遺伝子についてt検定を行った結果のt統計量とp値をoutに格納 p.value <- out[,2] #p値をp.valueに格納 q.value <- p.adjust(p.value, method="BH")#q値をq.valueに格納 ranking <- rank(p.value) #p.valueでランキングした結果をrankingに格納 sum(p.value < 0.0015) #p値が0.0015未満の遺伝子数を表示 #ファイルに保存 tmp <- cbind(rownames(data), data, p.value, q.value, ranking)#入力データの右側にp.value、q.value、rankingを結合した結果をtmpに格納。 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
3. サンプルデータ22のsample22.txtの場合:
10000行×6列分の標準正規分布に従う乱数です。G1群3サンプル vs. G2群3サンプルの2群間比較として解析を行っています。 乱数を発生させただけのデータなので、発現変動遺伝子(DEG)がない全てがnon-DEGのデータです。
in_f <- "sample22.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge3.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 3 #G1群のサンプル数を指定 param_G2 <- 3 #G2群のサンプル数を指定 #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #等分散性を仮定(var.equal=T)してt.testを行い、t統計量とp-valueの値を返す関数Students_ttestを作成。 Students_ttest <- function(x, cl){ x.class1 <- x[(cl == 1)] #ラベルが1のものをx.class1に格納 x.class2 <- x[(cl == 2)] #ラベルが2のものをx.class2に格納 if((sd(x.class1)+sd(x.class2)) == 0){#両方の群の標準偏差が共に0の場合は計算できないので... stat <- 0 #統計量を0 pval <- 1 #p値を1 return(c(stat, pval)) #として結果を返す } else{ #G1, G2どちらかの群の標準偏差が0(上記条件以外)の場合は hoge <- t.test(x.class1, x.class2, var.equal=T)#通常のt検定を行って、 return(c(hoge$statistic, hoge$p.value))#統計量とp値を結果として返す } } #本番 out <- t(apply(data, 1, Students_ttest, data.cl))#各(行)遺伝子についてt検定を行った結果のt統計量とp値をoutに格納 p.value <- out[,2] #p値をp.valueに格納 q.value <- p.adjust(p.value, method="BH")#q値をq.valueに格納 ranking <- rank(p.value) #p.valueでランキングした結果をrankingに格納 #ファイルに保存 tmp <- cbind(rownames(data), data, p.value, q.value, ranking)#入力データの右側にp.value、q.value、rankingを結合した結果をtmpに格納。 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
4. サンプルデータ23のsample23.txtの場合:
最初の3サンプルがG1群、残りの3サンプルがG2群の標準正規分布に従う乱数からなるシミュレーションデータです。 乱数発生後に、さらに最初の10% 分についてG1群に相当するところのみ数値を+3している(つまり10% がG1群で高発現というシミュレーションデータを作成している)
in_f <- "sample23.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge4.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 3 #G1群のサンプル数を指定 param_G2 <- 3 #G2群のサンプル数を指定 #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #等分散性を仮定(var.equal=T)してt.testを行い、t統計量とp-valueの値を返す関数Students_ttestを作成。 Students_ttest <- function(x, cl){ x.class1 <- x[(cl == 1)] #ラベルが1のものをx.class1に格納 x.class2 <- x[(cl == 2)] #ラベルが2のものをx.class2に格納 if((sd(x.class1)+sd(x.class2)) == 0){#両方の群の標準偏差が共に0の場合は計算できないので... stat <- 0 #統計量を0 pval <- 1 #p値を1 return(c(stat, pval)) #として結果を返す } else{ #G1, G2どちらかの群の標準偏差が0(上記条件以外)の場合は hoge <- t.test(x.class1, x.class2, var.equal=T)#通常のt検定を行って、 return(c(hoge$statistic, hoge$p.value))#統計量とp値を結果として返す } } #本番 out <- t(apply(data, 1, Students_ttest, data.cl))#各(行)遺伝子についてt検定を行った結果のt統計量とp値をoutに格納 p.value <- out[,2] #p値をp.valueに格納 q.value <- p.adjust(p.value, method="BH")#q値をq.valueに格納 ranking <- rank(p.value) #p.valueでランキングした結果をrankingに格納 #ファイルに保存 tmp <- cbind(rownames(data), data, p.value, q.value, ranking)#入力データの右側にp.value、q.value、rankingを結合した結果をtmpに格納。 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存 #以下は(こんなこともできますという)おまけ #(G1群 vs. G2群) t-testでp-value < 0.05を満たす遺伝子数を表示させたい場合: param4 <- 0.05 #閾値を指定 sum(p.value < param4) #p.valueが(param4)未満となっている要素数をsum関数を用いてカウントしている sum(q.value < 0.05) #FDR < 0.05を満たす要素数をsum関数を用いてカウントしている sum(q.value < 0.10) #FDR < 0.10を満たす要素数をsum関数を用いてカウントしている sum(q.value < 0.15) #FDR < 0.15を満たす要素数をsum関数を用いてカウントしている sum(q.value < 0.20) #FDR < 0.20を満たす要素数をsum関数を用いてカウントしている sum(q.value < 0.25) #FDR < 0.25を満たす要素数をsum関数を用いてカウントしている
5. サンプルデータ23のsample23.txtの場合:
4.と同じですが、関数の定義の仕方が異なります。
in_f <- "sample23.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge5.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 3 #G1群のサンプル数を指定 param_G2 <- 3 #G2群のサンプル数を指定 #必要な関数などをロード source("http://www.iu.a.u-tokyo.ac.jp/~kadota/R/R_functions.R")#Student's t-testを行うStudents_ttest関数を含むファイルをあらかじめ読み込む #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #本番 out <- t(apply(data, 1, Students_ttest, data.cl))#各(行)遺伝子についてt検定を行った結果のt統計量とp値をoutに格納 p.value <- out[,2] #p値をp.valueに格納 q.value <- p.adjust(p.value, method="BH")#q値をq.valueに格納 ranking <- rank(p.value) #p.valueでランキングした結果をrankingに格納 #ファイルに保存 tmp <- cbind(rownames(data), data, p.value, q.value, ranking)#入力データの右側にp.value、q.value、rankingを結合した結果をtmpに格納。 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存 #以下は(こんなこともできますという)おまけ #(G1群 vs. G2群) t-testでp-value < 0.05を満たす遺伝子数を表示させたい場合: param4 <- 0.05 #閾値を指定 sum(p.value < param4) #p.valueが(param4)未満となっている要素数をsum関数を用いてカウントしている sum(q.value < 0.05) #FDR < 0.05を満たす要素数をsum関数を用いてカウントしている sum(q.value < 0.10) #FDR < 0.10を満たす要素数をsum関数を用いてカウントしている sum(q.value < 0.15) #FDR < 0.15を満たす要素数をsum関数を用いてカウントしている sum(q.value < 0.20) #FDR < 0.20を満たす要素数をsum関数を用いてカウントしている sum(q.value < 0.25) #FDR < 0.25を満たす要素数をsum関数を用いてカウントしている
6. サンプルデータ23のsample23.txtの場合:
5.とほぼ同じですが、作業ディレクトリ中にStudents_ttest関数を含むR_functions.Rという名前のファイルが存在するという前提です。
in_f <- "sample23.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge6.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 3 #G1群のサンプル数を指定 param_G2 <- 3 #G2群のサンプル数を指定 #必要な関数などをロード source("R_functions.R") #Student's t-testを行うStudents_ttest関数を含むファイルをあらかじめ読み込む #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #本番 out <- t(apply(data, 1, Students_ttest, data.cl))#各(行)遺伝子についてt検定を行った結果のt統計量とp値をoutに格納 p.value <- out[,2] #p値をp.valueに格納 q.value <- p.adjust(p.value, method="BH")#q値をq.valueに格納 ranking <- rank(p.value) #p.valueでランキングした結果をrankingに格納 #ファイルに保存 tmp <- cbind(rownames(data), data, p.value, q.value, ranking)#入力データの右側にp.value、q.value、rankingを結合した結果をtmpに格納。 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存 #以下は(こんなこともできますという)おまけ #(G1群 vs. G2群) t-testでp-value < 0.05を満たす遺伝子数を表示させたい場合: param4 <- 0.05 #閾値を指定 sum(p.value < param4) #p.valueが(param4)未満となっている要素数をsum関数を用いてカウントしている sum(q.value < 0.05) #FDR < 0.05を満たす要素数をsum関数を用いてカウントしている sum(q.value < 0.10) #FDR < 0.10を満たす要素数をsum関数を用いてカウントしている sum(q.value < 0.15) #FDR < 0.15を満たす要素数をsum関数を用いてカウントしている sum(q.value < 0.20) #FDR < 0.20を満たす要素数をsum関数を用いてカウントしている sum(q.value < 0.25) #FDR < 0.25を満たす要素数をsum関数を用いてカウントしている
7. サンプルデータ22のsample22.txtの場合:
10000行×6列分の標準正規分布に従う乱数です。G1群3サンプル vs. G2群3サンプルの2群間比較として解析を行っています。 乱数を発生させただけのデータなので、発現変動遺伝子(DEG)がない全てがnon-DEGのデータです。
genefilterパッケージ中のrowttests関数を用いるやり方です。
in_f <- "sample22.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge7.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 3 #G1群のサンプル数を指定 param_G2 <- 3 #G2群のサンプル数を指定 #必要なパッケージをロード library(genefilter) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #本番 out <- rowttests(data, as.factor(data.cl))#各(行)遺伝子についてt検定を行った結果をoutに格納 p.value <- out$p.value #p値をp.valueに格納 q.value <- p.adjust(p.value, method="BH")#q値をq.valueに格納 ranking <- rank(p.value) #p.valueでランキングした結果をrankingに格納 #ファイルに保存 tmp <- cbind(rownames(data), data, p.value, q.value, ranking)#入力データの右側にp.value、q.value、rankingを結合した結果をtmpに格納。 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
解析 | 発現変動 | 2群間 | 対応なし | Welch t-test
不等分散性を仮定したt検定を用いて、2群間での発現変動遺伝子の同定を行うやり方を示します。
出力ファイルの「p.value」列がp値、「ranking」列がp値に基づく順位、「q.value」列が任意のFDR閾値を満たすものを調べるときに用いるものです。 実用上はq.value = FDRという理解で差し支えありません。例えば、「FDR < 0.05」を満たすものはq.valueが0.05未満のものに相当します。 p値を閾値とする際には有意水準5%などというという用語を用いますが、事実上「p < 0.05」などという表現を用いるのと同じです。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し、以下をコピペ
1. サンプルデータ16のsample16_log.txt(対数変換後のデータ)の場合:
クラスラベル情報ファイル(sample16_cl.txt)を利用するやり方です。
in_f1 <- "sample16_log.txt" #入力ファイル名(発現データ)を指定してin_f1に格納 in_f2 <- "sample16_cl.txt" #入力ファイル名(テンプレート情報)を指定してin_f2に格納 out_f <- "hoge1.txt" #出力ファイル名を指定してout_fに格納 #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f1, header=TRUE, row.names=1, sep="\t", quote="")#in_f1で指定したファイルの読み込み hoge <- read.table(in_f2, sep="\t", quote="")#in_f2で指定したファイルの読み込み data.cl <- hoge[,2] + 1 #テンプレートパターンベクトルhoge[,2]は0 or 1であるが、このウェブページではグループラベル情報を1 or 2で取り扱っているので、そうなるように全部に1を足した結果をdata.clに格納 #不等分散性を仮定(var.equal=F)してt.testを行い、t統計量とp-valueの値を返す関数Welch_ttestを作成。 Welch_ttest <- function(x, cl){ x.class1 <- x[(cl == 1)] #ラベルが1のものをx.class1に格納 x.class2 <- x[(cl == 2)] #ラベルが2のものをx.class2に格納 if((sd(x.class1)+sd(x.class2)) == 0){#両方の群の標準偏差が共に0の場合は計算できないので... stat <- 0 #統計量を0 pval <- 1 #p値を1 return(c(stat, pval)) #として結果を返す } else{ #G1, G2どちらかの群の標準偏差が0(上記条件以外)の場合は hoge <- t.test(x.class1, x.class2, var.equal=F)#通常のt検定を行って、 return(c(hoge$statistic, hoge$p.value))#統計量とp値を結果として返す } } #本番 out <- t(apply(data, 1, Welch_ttest, data.cl))#各(行)遺伝子についてt検定を行った結果のt統計量とp値をoutに格納 p.value <- out[,2] #p値をp.valueに格納 q.value <- p.adjust(p.value, method="BH")#q値をq.valueに格納 ranking <- rank(p.value) #p.valueでランキングした結果をrankingに格納 sum(p.value < 0.0015) #p値が0.0015未満の遺伝子数を表示 #ファイルに保存 tmp <- cbind(rownames(data), data, p.value, q.value, ranking)#入力データの右側にp.value、q.value、rankingを結合した結果をtmpに格納。 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存 tmp[order(ranking),] #rankingでソートした結果を表示
2. サンプルデータ16のsample16_log.txt(対数変換後のデータ)の場合:
クラスラベル情報ファイル(sample16_cl.txt)を利用しないやり方です。
in_f <- "sample16_log.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge2.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 6 #G1群のサンプル数を指定 param_G2 <- 5 #G2群のサンプル数を指定 #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #不等分散性を仮定(var.equal=F)してt.testを行い、t統計量とp-valueの値を返す関数Welch_ttestを作成。 Welch_ttest <- function(x, cl){ x.class1 <- x[(cl == 1)] #ラベルが1のものをx.class1に格納 x.class2 <- x[(cl == 2)] #ラベルが2のものをx.class2に格納 if((sd(x.class1)+sd(x.class2)) == 0){#両方の群の標準偏差が共に0の場合は計算できないので... stat <- 0 #統計量を0 pval <- 1 #p値を1 return(c(stat, pval)) #として結果を返す } else{ #G1, G2どちらかの群の標準偏差が0(上記条件以外)の場合は hoge <- t.test(x.class1, x.class2, var.equal=F)#通常のt検定を行って、 return(c(hoge$statistic, hoge$p.value))#統計量とp値を結果として返す } } #本番 out <- t(apply(data, 1, Welch_ttest, data.cl))#各(行)遺伝子についてt検定を行った結果のt統計量とp値をoutに格納 p.value <- out[,2] #p値をp.valueに格納 q.value <- p.adjust(p.value, method="BH")#q値をq.valueに格納 ranking <- rank(p.value) #p.valueでランキングした結果をrankingに格納 #ファイルに保存 tmp <- cbind(rownames(data), data, p.value, q.value, ranking)#入力データの右側にp.value、q.value、rankingを結合した結果をtmpに格納。 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
3. サンプルデータ22のsample22.txtの場合:
10000行×6列分の標準正規分布に従う乱数です。G1群3サンプル vs. G2群3サンプルの2群間比較として解析を行っています。 乱数を発生させただけのデータなので、発現変動遺伝子(DEG)がない全てがnon-DEGのデータです。
in_f <- "sample22.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge3.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 3 #G1群のサンプル数を指定 param_G2 <- 3 #G2群のサンプル数を指定 #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #不等分散性を仮定(var.equal=F)してt.testを行い、t統計量とp-valueの値を返す関数Welch_ttestを作成。 Welch_ttest <- function(x, cl){ x.class1 <- x[(cl == 1)] #ラベルが1のものをx.class1に格納 x.class2 <- x[(cl == 2)] #ラベルが2のものをx.class2に格納 if((sd(x.class1)+sd(x.class2)) == 0){#両方の群の標準偏差が共に0の場合は計算できないので... stat <- 0 #統計量を0 pval <- 1 #p値を1 return(c(stat, pval)) #として結果を返す } else{ #G1, G2どちらかの群の標準偏差が0(上記条件以外)の場合は hoge <- t.test(x.class1, x.class2, var.equal=F)#通常のt検定を行って、 return(c(hoge$statistic, hoge$p.value))#統計量とp値を結果として返す } } #本番 out <- t(apply(data, 1, Welch_ttest, data.cl))#各(行)遺伝子についてt検定を行った結果のt統計量とp値をoutに格納 p.value <- out[,2] #p値をp.valueに格納 q.value <- p.adjust(p.value, method="BH")#q値をq.valueに格納 ranking <- rank(p.value) #p.valueでランキングした結果をrankingに格納 #ファイルに保存 tmp <- cbind(rownames(data), data, p.value, q.value, ranking)#入力データの右側にp.value、q.value、rankingを結合した結果をtmpに格納。 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
4. 入力データがdata_Singh_RMA_3274.txtの場合1:
in_f <- "data_Singh_RMA_3274.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge4.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 50 #G1群のサンプル数を指定 param_G2 <- 52 #G2群のサンプル数を指定 #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #不等分散性を仮定(var.equal=F)してt.testを行い、t統計量とp-valueの値を返す関数Welch_ttestを作成。 Welch_ttest <- function(x, cl){ x.class1 <- x[(cl == 1)] #ラベルが1のものをx.class1に格納 x.class2 <- x[(cl == 2)] #ラベルが2のものをx.class2に格納 if((sd(x.class1)+sd(x.class2)) == 0){#両方の群の標準偏差が共に0の場合は計算できないので... stat <- 0 #統計量を0 pval <- 1 #p値を1 return(c(stat, pval)) #として結果を返す } else{ #G1, G2どちらかの群の標準偏差が0(上記条件以外)の場合は hoge <- t.test(x.class1, x.class2, var.equal=F)#通常のt検定を行って、 return(c(hoge$statistic, hoge$p.value))#統計量とp値を結果として返す } } #本番 out <- t(apply(data, 1, Welch_ttest, data.cl))#各(行)遺伝子についてt検定を行った結果のt統計量とp値をoutに格納 p.value <- out[,2] #p値をp.valueに格納 q.value <- p.adjust(p.value, method="BH")#q値をq.valueに格納 ranking <- rank(p.value) #p.valueでランキングした結果をrankingに格納 #ファイルに保存 tmp <- cbind(rownames(data), data, p.value, q.value, ranking)#入力データの右側にp.value、q.value、rankingを結合した結果をtmpに格納。 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
5. 入力データがdata_Singh_RMA_3274.txtの場合(関数の定義の部分が少し違うだけです):
in_f <- "data_Singh_RMA_3274.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge5.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 50 #G1群のサンプル数を指定 param_G2 <- 52 #G2群のサンプル数を指定 #必要な関数などをロード source("http://www.iu.a.u-tokyo.ac.jp/~kadota/R/R_functions.R")#Welch t-testを行うWelch_ttest関数を含むファイルをあらかじめ読み込む #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #本番 out <- t(apply(data, 1, Welch_ttest, data.cl))#各(行)遺伝子についてt検定を行った結果のt統計量とp値をoutに格納 p.value <- out[,2] #p値をp.valueに格納 q.value <- p.adjust(p.value, method="BH")#q値をq.valueに格納 ranking <- rank(p.value) #p.valueでランキングした結果をrankingに格納 #ファイルに保存 tmp <- cbind(rownames(data), data, p.value, q.value, ranking)#入力データの右側にp.value、q.value、rankingを結合した結果をtmpに格納。 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
解析 | 発現変動 | 2群間 | 対応なし | Mann-Whitney U-test
Mann-Whitney(マンホイットニー; MW) U検定を用いて、2群間での発現変動遺伝子の同定を行う。入力データは対数変換(log2変換)後のものを例として使用してはいますが、この方法はノンパラメトリックな方法なので、対数変換していようがいまいが同じ結果を返すので、特に気にする必要はありません。
出力ファイルの「p.value」列がp値、「ranking」列がp値に基づく順位、「q.value」列が任意のFDR閾値を満たすものを調べるときに用いるものです。 実用上はq.value = FDRという理解で差し支えありません。例えば、「FDR < 0.05」を満たすものはq.valueが0.05未満のものに相当します。 p値を閾値とする際には有意水準5%などというという用語を用いますが、事実上「p < 0.05」などという表現を用いるのと同じです。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し、以下をコピペ
1. 入力データがdata_Singh_RMA_3274.txtの場合:
in_f <- "data_Singh_RMA_3274.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge1.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 50 #G1群のサンプル数を指定 param_G2 <- 52 #G2群のサンプル数を指定 #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #MWのU検定を行い、t統計量とp-valueの値を返す関数MW_Utestを作成。 MW_Utest <- function(x, cl){ x.class1 <- x[(cl == 1)] #ラベルが1のものをx.class1に格納 x.class2 <- x[(cl == 2)] #ラベルが2のものをx.class2に格納 hoge <- wilcox.test(x.class1, x.class2)#MWのU検定を行って、 return(c(hoge$statistic, hoge$p.value))#統計量とp値を結果として返す } #本番 out <- t(apply(data, 1, MW_Utest, data.cl))#各(行)遺伝子についてMWのU検定を行った結果の統計量とp値をoutに格納 p.value <- out[,2] #p値をp.valueに格納 q.value <- p.adjust(p.value, method="BH")#q値をq.valueに格納 ranking <- rank(p.value) #p.valueでランキングした結果をrankingに格納 sum(p.value < 0.0015) #p値が0.0015未満の遺伝子数を表示 #ファイルに保存 tmp <- cbind(rownames(data), data, p.value, q.value, ranking)#入力データの右側にp.value、q.value、rankingを結合した結果をtmpに格納。 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存 head(tmp[order(ranking),]) #rankingでソートした結果(の一部)を表示
2. 入力データがdata_Singh_RMA_3274.txtの場合(関数の定義の部分が少し違うだけです):
in_f <- "data_Singh_RMA_3274.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge2.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 50 #G1群のサンプル数を指定 param_G2 <- 52 #G2群のサンプル数を指定 #必要な関数などをロード source("http://www.iu.a.u-tokyo.ac.jp/~kadota/R/R_functions.R")#Student's t-testを行うWelch_ttest関数を含むファイルをあらかじめ読み込む #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #本番 out <- t(apply(data, 1, MW_Utest, data.cl))#各(行)遺伝子についてMWのU検定を行った結果の統計量とp値をoutに格納 p.value <- out[,2] #p値をp.valueに格納 q.value <- p.adjust(p.value, method="BH")#q値をq.valueに格納 ranking <- rank(p.value) #p.valueでランキングした結果をrankingに格納 #ファイルに保存 tmp <- cbind(rownames(data), data, p.value, q.value, ranking)#入力データの右側にp.value、q.value、rankingを結合した結果をtmpに格納。 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
解析 | 発現変動 | 2群間 | 対応なし | パターンマッチング法
パターンマッチング法を用いて、2群間での発現変動遺伝子の同定を行うやり方を紹介します。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し、以下をコピペ
1. サンプルデータ16のsample16_log.txt(対数変換後のデータ)の場合:
クラスラベル情報ファイル(sample16_cl.txt)を利用するやり方です。
in_f1 <- "sample16_log.txt" #入力ファイル名を指定してin_f1に格納(発現データ) in_f2 <- "sample16_cl.txt" #入力ファイル名を指定してin_f2に格納(テンプレート情報) out_f <- "hoge1.txt" #出力ファイル名を指定してout_fに格納 param <- "pearson" #相関係数の種類を指定("pearson"または"spearman") #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f1, header=TRUE, row.names=1, sep="\t", quote="")#in_f1で指定したファイルの読み込み hoge <- read.table(in_f2, sep="\t", quote="")#in_f2で指定したファイルの読み込み data.cl <- hoge[,2] #テンプレートパターンベクトルdata.clを作成 #本番 r <- apply(data, 1, cor, y=data.cl, method=param)#各(行)遺伝子についてテンプレートパターンdata.clとの相関係数を計算した結果をrに格納 #ファイルに保存 tmp <- cbind(rownames(data), data, r) #入力データの右側に相関係数rのベクトルを結合した結果をtmpに格納。 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
2. サンプルデータ16のsample16_log.txt(対数変換後のデータ)の場合:
クラスラベル情報ファイル(sample16_cl.txt)を利用しないやり方です。
in_f <- "sample16_log.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge2.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 6 #G1群のサンプル数を指定 param_G2 <- 5 #G2群のサンプル数を指定 param <- "pearson" #相関係数の種類を指定("pearson"または"spearman") #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #本番 r <- apply(data, 1, cor, y=data.cl, method=param)#各(行)遺伝子についてテンプレートパターンdata.clとの相関係数を計算した結果をrに格納 #ファイルに保存 tmp <- cbind(rownames(data), data, r) #入力データの右側に相関係数rのベクトルを結合した結果をtmpに格納。 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
解析 | 発現変動 | 2群間 | 対応あり | について
手持ちのアレイデータが以下のような場合にこのカテゴリーに属す方法を適用します(当然比較する二群のサンプル数は同じであるべき!):
Aさんの正常サンプル
Bさんの正常サンプル
Cさんの正常サンプル
...
Aさんの癌サンプル
Bさんの癌サンプル
Cさんの癌サンプル
...
ここでは二つの方法を紹介しています。
一つは有名なSAM(Tusher et al., 2001)のやりかたです。
もう一つはSAMで得られた統計量を基本としつつ、シグナル強度が高い遺伝子を上位にランキングするように重みをかけた統計量を返すやり方です。
これはWAD統計量(Kadota et al., 2008)の重みの項だけをSAM統計量にかけた、いわばweighted SAM統計量です。
WAD統計量はAD統計量×weightで得られるものですが、the weighted SAM統計量 = SAM統計量×weightとして計算しています。
このweightの計算はいたってシンプルです。例えば計5遺伝子しかないとして、「gene1の対数変換後の平均シグナル強度が8, gene2の〜5, gene3の〜7, gene4の〜11, gene5の〜2」だったとすると、最も平均シグナル強度が高い遺伝子のweight=1, 最も低い遺伝子のweight=0のように規格化しているだけです。
つまり、
- gene1のweight = (8 - min(8, 5, 7, 11, 2))/(max(8, 5, 7, 11, 2) - min(8, 5, 7, 11, 2)) = (8 - 2)/(11 - 2) = 0.6666...
- gene2のweight = (5 - 2)/(11 - 2) = 0.3333...
- gene3のweight = (7 - 2)/(11 - 2) = 0.5555...
- gene4のweight = (11 - 2)/(11 - 2) = 1
- gene5のweight = (2 - 2)/(11 - 2) = 0
です。相対平均シグナル強度をweightとしているだけです。
ただし、G1群, G2群のサンプル数の違いを考慮する必要はあるので「平均シグナル強度= (mean(A) + mean(B))/2」です。
解析 | 発現変動 | 2群間 | 対応あり | SAM (Tusher_2001)
Significance Analysis of Microarrays (SAM)法で「対応ありの2群間比較(two-class paired)」を行う。
ここでは例題として用いた102サンプルからなるファイル(data_Singh_RMA_3274.txt)のラベル情報が以下のようになっていると仮定します:
症例 1さんの正常サンプル 症例 2さんの正常サンプル ... 症例51さんの正常サンプル 症例 1さんの腫瘍サンプル 症例 2さんの腫瘍サンプル ... 症例51さんの腫瘍サンプル
また、このファイルはすでに底が2でlog変換されているものとします(logged2=TRUE)。
「ファイル」−「ディレクトリの変更」で解析したいファイル(data_Singh_RMA_3274.txt)を置いてあるディレクトリに移動し、以下をコピペ
in_f <- "data_Singh_RMA_3274.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge.txt" #出力ファイル名を指定してout_fに格納 param1 <- 51 #症例数を指定 param_perm <- 60 #並べ替え回数を指定(数値が大きいほどより正確だがその分だけ時間がかかる。実際の解析ではサンプル数にもよるが最低でも1000以上を推奨) #必要なパッケージをロード library(samr) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(-(1:param1), 1:param1) #症例の正常と腫瘍サンプルを対にして情報を与えたベクトルdata.clを作成(症例1の正常が-1、腫瘍が1などという感じで同じ数字のプラスとマイナスで対になっていることを認識させている) #本番 data.tmp <- list(x=as.matrix(data), #SAMを実行するsamr関数の入力フォーマットに合わせたdata.tmpを作成 y=data.cl, #SAMを実行するsamr関数の入力フォーマットに合わせたdata.tmpを作成 geneid=rownames(data), #SAMを実行するsamr関数の入力フォーマットに合わせたdata.tmpを作成 genenames=rownames(data),#SAMを実行するsamr関数の入力フォーマットに合わせたdata.tmpを作成 logged2=TRUE) #SAMを実行するsamr関数の入力フォーマットに合わせたdata.tmpを作成 out <- samr(data.tmp, resp.type="Two class paired", nperms=param_perm)#samr関数を実行し、結果をoutに格納。 summary(out) #outからどのような情報が抜き出せるか調べる。 p.value <- samr.pvalues.from.perms(out$tt, out$ttstar)#p値をp.valueに格納 q.value <- p.adjust(p.value, method="BH")#q値をq.valueに格納 ranking <- rank(p.value) #p.valueでランキングした結果をrankingに格納 stat_fc <- log2(out$foldchange) #log(FC)統計量をstat_fcに格納 rank_fc <- rank(-abs(stat_fc)) #統計量の絶対値でランキングした結果をrank_fcに格納 #ファイルに保存 tmp <- cbind(rownames(data), data, p.value, q.value, ranking, stat_fc, rank_fc)#入力データの右側にp.value、q.value、ranking、log(G2/G1)、log(G2/G1)の順位を結合した結果をtmpに格納。 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
解析 | 発現変動 | 2群間 | 対応あり | SAM (Tusher_2001)+WADの重みづけ
Significance Analysis of Microarrays (SAM)法で「対応ありの2群間比較(two-class paired)」を行う。
が、WAD (Kadota_2008)を知っている人は「シグナル強度が高い遺伝子を上位に来るようにランキングしたい」と思います。そこで、上記SAM統計量にWADの重みの項(weight)をかけた統計量を返すやり方をここでは紹介しています。
下記を行って得られるhoge.txt中のweight列がWADの重みの項になります。結果として得たい統計量およびランキング結果はstat_sam_wadおよびrank_sam_wadの列になります。確かに全体としてシグナル強度が高い遺伝子が上位にランクされていることがおわかりいただけると思います。
ここでは例題として用いた102サンプルからなるファイル(data_Singh_RMA_3274.txt)のラベル情報が以下のようになっていると仮定します:
症例 1さんの正常サンプル 症例 2さんの正常サンプル ... 症例51さんの正常サンプル 症例 1さんの腫瘍サンプル 症例 2さんの腫瘍サンプル ... 症例51さんの腫瘍サンプル
また、このファイルはすでに底が2でlog変換されているものとします(logged2=TRUE)。
「ファイル」−「ディレクトリの変更」で解析したいファイル(data_Singh_RMA_3274.txt)を置いてあるディレクトリに移動し、以下をコピペ
in_f <- "data_Singh_RMA_3274.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge.txt" #出力ファイル名を指定してout_fに格納 param1 <- 51 #症例数を指定 param_perm <- 60 #並べ替え回数を指定(数値が大きいほどより正確だがその分だけ時間がかかる。実際の解析ではサンプル数にもよるが最低でも1000以上を推奨) #必要なパッケージをロード library(samr) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(-(1:param1), 1:param1) #症例の正常と腫瘍サンプルを対にして情報を与えたベクトルdata.clを作成(症例1の正常が-1、腫瘍が1などという感じで同じ数字のプラスとマイナスで対になっていることを認識させている) #本番 data.tmp = list(x=as.matrix(data), y=data.cl, geneid=rownames(data), genenames=rownames(data), logged2=TRUE)#SAMを実行するsamr関数の入力フォーマットに合わせたdata.tmpを作成 out <- samr(data.tmp, resp.type="Two class paired", nperms=param_perm)#samr関数を実行し、結果をoutに格納。 stat_sam <- out$tt #SAM統計量をstat_samに格納 rank_sam <- rank(-abs(stat_sam)) #統計量の絶対値でランキングした結果をrank_samに格納 data.cl <- c(rep(1, param1), rep(2, param1))#G1群を1、G2群を2としたベクトルdata.clを作成 tmp.class1 <- apply(data[,data.cl == 1], 1, mean)#G1群の(遺伝子ごとの)平均シグナル強度を計算 tmp.class2 <- apply(data[,data.cl == 2], 1, mean)#G2群の(遺伝子ごとの)平均シグナル強度を計算 ave_vector <- (tmp.class1 + tmp.class2)/2#全サンプルの(遺伝子ごとの)平均シグナル強度を計算しave_vectorに格納 dr <- max(ave_vector) - min(ave_vector)#全サンプルの(遺伝子ごとの)平均シグナル強度のダイナミックレンジ(最大値-最小値)を計算しdrに格納 weight <- (ave_vector - min(ave_vector))/dr#WADの重みの項を計算しweightに格納 stat_sam_wad <- stat_sam*weight #SAM統計量にWADの重みの項をかけたもの(stat_sam*weight)を計算しstat_sam_wadに格納 rank_sam_wad <- rank(-abs(stat_sam_wad))#the weighted SAM統計量(stat_sam_wad)の絶対値でランキングした結果をrank_sam_wadに格納 #ファイルに保存 tmp <- cbind(rownames(data), data, stat_sam, rank_sam, weight, stat_sam_wad, rank_sam_wad)#入力データの右側に「SAM統計量」「その順位」「weight」「weighted SAM統計量(=SAM*weitht)」「その順位」を結合した結果をtmpに格納。 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
解析 | 発現変動 | 2群間 | 対応あり | 時系列 | について
手持ちのアレイデータが以下のような場合にこのカテゴリーに属す方法を適用します:
サンプルAの薬剤投与0h後 サンプルAの薬剤投与2h後 サンプルAの薬剤投与4h後 サンプルBの薬剤投与0h後 サンプルBの薬剤投与2h後 サンプルBの薬剤投与4h後
2013年6月に調査した結果をリストアップします。
解析 | 発現変動 | 時系列 | についてにリストアップした方法の中にも、このカテゴリーに属する解析が可能なものがあるかもしれません:
解析 | 発現変動 | 2群間 | 対応あり | 時系列 | maSigPro (Conesa_2006)
maSigProパッケージ(Conesa et al., 2006)を用いて
時系列データの中から統計的に有意な発現の異なるプロファイルを検出します。おそらく以下のコマンドで抽出するやり方でいいと思います。
サンプルデータで示すような「Control (A)の時系列データ」と
「Cold (B)の時系列データ」が手元にあり、「A vs. Bで発現の異なる遺伝子」を検出したいときに利用します。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し、以下をコピペ
1. サンプルデータのsample10_2groups.txtと実験デザインファイル(sample10_2groups_cl.txt)の場合:
in_f1 <- "sample10_2groups.txt" #入力ファイル名(発現データファイル)を指定してin_f1に格納 in_f2 <- "sample10_2groups_cl.txt" #入力ファイル名(実験デザインファイル)を指定してin_f2に格納 out_f <- "hoge.txt" #出力ファイル名を指定してout_fに格納 param_FDR <- 0.05 #false discovery rate (FDR)閾値を指定 #必要なパッケージをロード library(maSigPro) #パッケージの読み込み #データファイルの読み込み data <- read.table(in_f1, header=TRUE, row.names=1, sep="\t", quote="")#in_f1で指定したファイルの読み込み edesign <- read.table(in_f2, header=TRUE, row.names=1, sep="\t", quote="")#in_f2で指定したファイルの読み込み #本番(発現変動遺伝子検出; ANOVAみたいなところ) design <- make.design.matrix(edesign, degree=2,#実験デザイン行列の作成。degree=2は、2次の回帰モデルで考えることを意味する time.col=1, #time.col=1の1は、1列目がtime情報であることを示す repl.col=2, #repl.col=2の2は、2列目がreplicates情報であることを示す group.cols=c(3:ncol(edesign)))#group.cols=c(3:ncol(edesign)))の3は、3列目以降の情報がgroup情報であることを示す fit <- p.vector(data, design, Q=param_FDR)#回帰モデルの作成 fit$i #指定したFDR閾値を満たす発現変動遺伝子(DEG)数を表示 fit$BH.alfa #指定したFDR閾値に相当するp-valueを表示 fit$SELEC #DEGとされたものの発現情報を表示(DEG数が多い場合には画面が一気に流れる) #本番(発現変動パターン検出; post-hoc testみたいなところ) hoge <- T.fit(fit, alfa=param_FDR) #geneごとに最もよい回帰モデルを選択した結果をhogeに格納 hoge$sol #結果のsummaryを表示。p-value列がANOVA p-value。右のほうのがpost-hoc testのどのモデルで違いがあったかを調べるためのp-value。 out <- get.siggenes(hoge, rsq=0.7, vars="groups")#回帰モデルのRsquaredの値が0.7(この値がデフォルト)よりも大きいものを抽出し、outに格納 gene_id <- out$summary$BvsA[1:out$sig.genes$BvsA$g]#発現変動遺伝子のIDをgene_idに格納。 gene_profile <- out$sig.genes$BvsA$sig.profiles#発現変動遺伝子の発現プロファイルをgene_profileに格納。 p.value <- out$sig.genes$BvsA$sig.pvalues[,1]#p値をp.valueに格納。 ranking <- rank(abs(p.value)) #p値の順位をrankingに格納。 #ファイルに保存 tmp <- cbind(gene_id, gene_profile, p.value, ranking)#保存したい情報をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存 #以下は(こんなこともできますという)おまけ #発現変動の度合いでソートした結果を得たい場合: out_f2 <- "hoge2.txt" #出力ファイル名を指定してout_fに格納 tmp2 <- tmp[order(ranking),] #順位(ranking)でソートした結果をtmp2に格納 write.table(tmp2, out_f2, sep="\t", append=F, quote=F, row.names=F)#tmp2の中身を指定したファイル名で保存
解析 | 発現変動 | 3群間 | 対応なし |について
手持ちのアレイデータが以下のような場合にこのカテゴリーに属す方法を適用します:
AさんのControlサンプル BさんのControlサンプル CさんのControlサンプル Dさんの薬剤X刺激後サンプル Eさんの薬剤X刺激後サンプル Fさんの薬剤X刺激後サンプル Gさんの薬剤X刺激後サンプル Hさんの薬剤Y刺激後サンプル Iさんの薬剤Y刺激後サンプル Jさんの薬剤Y刺激後サンプル
R用:
R以外:
解析 | 発現変動 | 3群間 | 対応なし | Mulcom (Isella_2011)
Mulcomパッケージを用いて3群間比較を行うやり方を示します。とりあえず項目のみ。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し、以下をコピペ
1. :
in_f <- "sample2_log.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge1.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 3 #G1群のサンプル数を指定 param_G2 <- 3 #G2群のサンプル数を指定 param_G3 <- 5 #G3群のサンプル数を指定 #必要なパッケージをロード library(Mulcom) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2), rep(3, param_G3))#G1群を1、G2群を2、G3群を3としたベクトルdata.clを作成
解析 | 発現変動 | 3群間 | 対応なし | 基礎 | limma (Ritchie_2015)
limmaパッケージを用いて3群間比較を行うやり方を示します。 ここでやっていることはANOVAのような「どこかの群間で発現に差がある遺伝子を検出」です。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し、以下をコピペ
1. サンプルデータ25の10,000 genes×9 samplesのsample25.txtの場合:
シミュレーションデータ(G1群3サンプル vs. G2群3サンプル vs. G3群3サンプル)です。 gene_1〜gene_3000までがDEG (gene_1〜gene_1000がG1群で高発現、gene_1001〜gene_2000がG2群で高発現、gene_001〜gene_3000がG3群で高発現) gene_3001〜gene_10000までがnon-DEGであることが既知です。 FDR閾値を満たす遺伝子数は、5%で2,892個、1%で2,450個と妥当な結果が得られています。
in_f <- "sample25.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge1.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 3 #G1群のサンプル数を指定 param_G2 <- 3 #G2群のサンプル数を指定 param_G3 <- 3 #G3群のサンプル数を指定 #必要なパッケージをロード library(limma) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2), rep(3, param_G3))#G1群を1、G2群を2、G3群を3としたベクトルdata.clを作成 #本番(DEG検出) design <- model.matrix(~ as.factor(data.cl))#デザイン行列を作成した結果をdesignに格納 fit <- lmFit(data, design) #モデル構築 out <- eBayes(fit) #検定(経験ベイズ) hoge <- topTable(out, coef=2:3, n=nrow(data), sort.by="none")#解析結果を抽出してhogeに格納 p.value <- hoge$P.Value #p値をp.valueに格納 q.value <- hoge$adj.P.Val #q値をq.valueに格納 ranking <- rank(p.value) #p.valueでランキングした結果をrankingに格納 #ファイルに保存 tmp <- cbind(rownames(data), data, p.value, q.value, ranking)#入力データの右側にp.value、q.value、rankingを結合した結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
2. サンプルデータ20の31,099 probesets×24 samplesのRMA-preprocessedデータ(data_rma_2.txt)の場合:
Affymetrix Rat Genome 230 2.0 Arrayを用いて得られたNakai et al., BBB, 2008のデータです。 8 褐色脂肪(BAT) vs. 8 白色脂肪(WAT) vs. 8 肝臓(LIV)の3群間比較用データとして取り扱います。 FDR 1%閾値を満たす遺伝子数は19,485個と非常に多いことが分かります。
in_f <- "data_rma_2.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge2.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 8 #G1群のサンプル数を指定 param_G2 <- 8 #G2群のサンプル数を指定 param_G3 <- 8 #G3群のサンプル数を指定 #必要なパッケージをロード library(limma) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2), rep(3, param_G3))#G1群を1、G2群を2、G3群を3としたベクトルdata.clを作成 #本番(DEG検出) design <- model.matrix(~ as.factor(data.cl))#デザイン行列を作成した結果をdesignに格納 fit <- lmFit(data, design) #モデル構築 out <- eBayes(fit) #検定(経験ベイズ) hoge <- topTable(out, coef=2:3, n=nrow(data), sort.by="none")#解析結果を抽出してhogeに格納 p.value <- hoge$P.Value #p値をp.valueに格納 q.value <- hoge$adj.P.Val #q値をq.valueに格納 ranking <- rank(p.value) #p.valueでランキングした結果をrankingに格納 #ファイルに保存 tmp <- cbind(rownames(data), data, p.value, q.value, ranking)#入力データの右側にp.value、q.value、rankingを結合した結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
解析 | 発現変動 | 3群間 | 対応なし | 応用1 | limma (Ritchie_2015)
limmaパッケージを用いて3群間比較を行うやり方を示します。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し、以下をコピペ
1. サンプルデータ25の10,000 genes×9 samplesのsample25.txtの場合:
シミュレーションデータ(G1群3サンプル vs. G2群3サンプル vs. G3群3サンプル)です。 gene_1〜gene_3000までがDEG (gene_1〜gene_1000がG1群で高発現、gene_1001〜gene_2000がG2群で高発現、gene_001〜gene_3000がG3群で高発現) gene_3001〜gene_10000までがnon-DEGであることが既知です。 ANOVAと同じく、どこかの群間で発現変動しているものを検出するやり方(帰無仮説: G1 = G2 = G3)です。 出力ファイルのq.value列を眺めると、DEGに相当する最初の1行目から3000行目のところのほとんどのq.valueが0.1程度未満、 それ以外の3001から10000行のほとんどのq.valueが比較的大きな数値なっていることからparam_coefでの指定方法が妥当であることが分かります。
in_f <- "sample25.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge1.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 3 #G1群のサンプル数を指定 param_G2 <- 3 #G2群のサンプル数を指定 param_G3 <- 3 #G3群のサンプル数を指定 param_coef <- c(2, 3) #デザイン行列中の除きたい列を指定 #必要なパッケージをロード library(limma) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2), rep(3, param_G3))#G1群を1、G2群を2、G3群を3としたベクトルdata.clを作成 #本番(DEG検出) design <- model.matrix(~ as.factor(data.cl))#デザイン行列を作成した結果をdesignに格納 fit <- lmFit(data, design) #モデル構築 out <- eBayes(fit) #検定(経験ベイズ) hoge <- topTable(out, coef=param_coef, n=nrow(data), sort.by="none")#解析結果を抽出してhogeに格納 p.value <- hoge$P.Value #p値をp.valueに格納 q.value <- hoge$adj.P.Val #q値をq.valueに格納 ranking <- rank(p.value) #p.valueでランキングした結果をrankingに格納 #ファイルに保存 tmp <- cbind(rownames(data), data, p.value, q.value, ranking)#入力データの右側にp.value、q.value、rankingを結合した結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
2. サンプルデータ25の10,000 genes×9 samplesのsample25.txtの場合:
「G1群 vs. G2群」の比較を行いたいときの指定方法(帰無仮説: G1 = G2)です。 出力ファイルのq.value列を眺めると、DEGに相当する最初の1行目から2000行目のところのほとんどのq.valueが0.1程度未満、 それ以外の2001から10000行のほとんどのq.valueが比較的大きな数値なっていることからparam_coefでの指定方法が妥当であることが分かります。 「full modelに相当するデザイン行列designの2列目のパラメータを除いたものをreduced modelとする」という指定に相当します。
in_f <- "sample25.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge2.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 3 #G1群のサンプル数を指定 param_G2 <- 3 #G2群のサンプル数を指定 param_G3 <- 3 #G3群のサンプル数を指定 param_coef <- 2 #デザイン行列中の除きたい列を指定 #必要なパッケージをロード library(limma) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2), rep(3, param_G3))#G1群を1、G2群を2、G3群を3としたベクトルdata.clを作成 #本番(DEG検出) design <- model.matrix(~ as.factor(data.cl))#デザイン行列を作成した結果をdesignに格納 fit <- lmFit(data, design) #モデル構築 out <- eBayes(fit) #検定(経験ベイズ) hoge <- topTable(out, coef=param_coef, n=nrow(data), sort.by="none")#解析結果を抽出してhogeに格納 p.value <- hoge$P.Value #p値をp.valueに格納 q.value <- hoge$adj.P.Val #q値をq.valueに格納 ranking <- rank(p.value) #p.valueでランキングした結果をrankingに格納 #ファイルに保存 tmp <- cbind(rownames(data), data, p.value, q.value, ranking)#入力データの右側にp.value、q.value、rankingを結合した結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
3. サンプルデータ25の10,000 genes×9 samplesのsample25.txtの場合:
「G1群 vs. G3群」の比較を行いたいときの指定方法(帰無仮説: G1 = G3)です。 出力ファイルのq.value列を眺めると、DEGに相当する最初の1-1000行目および2001-3000行目のところのほとんどのq.valueが0.1程度未満、 G2群で高発現DEGの1001から2000行目のほとんどのq.valueが比較的大きな数値になっていることからparam_coefでの指定方法が妥当であることが分かります。 「full modelに相当するデザイン行列designの3列目のパラメータを除いたものをreduced modelとする」という指定に相当します。
in_f <- "sample25.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge3.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 3 #G1群のサンプル数を指定 param_G2 <- 3 #G2群のサンプル数を指定 param_G3 <- 3 #G3群のサンプル数を指定 param_coef <- 3 #デザイン行列中の除きたい列を指定 #必要なパッケージをロード library(limma) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2), rep(3, param_G3))#G1群を1、G2群を2、G3群を3としたベクトルdata.clを作成 #本番(DEG検出) design <- model.matrix(~ as.factor(data.cl))#デザイン行列を作成した結果をdesignに格納 fit <- lmFit(data, design) #モデル構築 out <- eBayes(fit) #検定(経験ベイズ) hoge <- topTable(out, coef=param_coef, n=nrow(data), sort.by="none")#解析結果を抽出してhogeに格納 p.value <- hoge$P.Value #p値をp.valueに格納 q.value <- hoge$adj.P.Val #q値をq.valueに格納 ranking <- rank(p.value) #p.valueでランキングした結果をrankingに格納 #ファイルに保存 tmp <- cbind(rownames(data), data, p.value, q.value, ranking)#入力データの右側にp.value、q.value、rankingを結合した結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
4. サンプルデータ25の10,000 genes×9 samplesのsample25.txtの場合:
「G2群 vs. G3群」の比較を行いたいときの指定方法(帰無仮説: G2 = G3)です。 出力ファイルのq.value列を眺めると、DEGに相当する最初の1001-3000行目のところのほとんどのq.valueが0.1程度未満である一方、 G1群で高発現DEGの1から1000行目のほとんどq.valueが比較的大きな数値となっていることから、param_contrastでの指定方法が妥当であることが分かります。 1-3.のようにparam_coefの枠組みではうまくG2 vs. G3をうまく表現できないので、コントラストという別の枠組みで指定しています。 思考回路としては、「a1*G1 + a2*G2 + a3*G3 = 0」として、この場合の目的である「G2 = G3という帰無仮説」を作成できるように、係数a1, a2, a3に適切な数値を代入することです。 ここではa1 = 0、a2 = -1, a3 = 1にすることで目的の帰無仮説を作成できます。 以下ではc(0, -1, 1)と指定していますが、 c(0, 1, -1)でも構いません。 理由はどちらでもG2 = G3を表現できているからです。 尚、full modelに相当するデザイン行列の作成手順も若干異なります。具体的には、model.matrix関数実行時に「0 + 」を追加しています。 これによって、最初の1列目が全て1になるようなG1群を基準にして作成したデザイン行列ではなく、各群が各列になるようにしています。
in_f <- "sample25.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge4.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 3 #G1群のサンプル数を指定 param_G2 <- 3 #G2群のサンプル数を指定 param_G3 <- 3 #G3群のサンプル数を指定 param_contrast <- c(0, -1, 1) #コントラスト情報を指定(reduced model作成用) #必要なパッケージをロード library(limma) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2), rep(3, param_G3))#G1群を1、G2群を2、G3群を3としたベクトルdata.clを作成 #本番(DEG検出) design <- model.matrix(~ 0 + as.factor(data.cl))#デザイン行列を作成した結果をdesignに格納 fit <- lmFit(data, design) #モデル構築 fit2 <- contrasts.fit(fit, contrasts=param_contrast)#コントラスト情報を与えている out <- eBayes(fit2) #検定(経験ベイズ) hoge <- topTable(out, n=nrow(data), sort.by="none")#解析結果を抽出してhogeに格納 p.value <- hoge$P.Value #p値をp.valueに格納 q.value <- hoge$adj.P.Val #q値をq.valueに格納 ranking <- rank(p.value) #p.valueでランキングした結果をrankingに格納 #ファイルに保存 tmp <- cbind(rownames(data), data, p.value, q.value, ranking)#入力データの右側にp.value、q.value、rankingを結合した結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
5. サンプルデータ25の10,000 genes×9 samplesのsample25.txtの場合:
「G1群 vs. G2群」の比較を行いたいときの指定方法(帰無仮説: G1 = G2)です。 出力ファイルのq.value列を眺めると、DEGに相当する最初の1-2000行目のところのほとんどのq.valueが0.1程度未満である一方、 G3群で高発現DEGの2001から3000行目のほとんどq.valueが比較的大きな数値となっていることから、param_contrastでの指定方法が妥当であることが分かります。 1-3.のようにparam_coefの枠組みではうまくG2 vs. G3をうまく表現できないので、コントラストという別の枠組みで指定しています。 思考回路としては、「a1*G1 + a2*G2 + a3*G3 = 0」として、この場合の目的である「G1 = G2という帰無仮説」を作成できるように、係数a1, a2, a3に適切な数値を代入することです。 ここではa1 = 1、a2 = -1, a3 = 0にすることで目的の帰無仮説を作成できます。 以下ではc(1, -1, 0)と指定していますが、 c(-1, 1, 0)でも構いません。理由はどちらでもG1 = G2を表現できているからです。
in_f <- "sample25.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge5.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 3 #G1群のサンプル数を指定 param_G2 <- 3 #G2群のサンプル数を指定 param_G3 <- 3 #G3群のサンプル数を指定 param_contrast <- c(1, -1, 0) #コントラスト情報を指定(reduced model作成用) #必要なパッケージをロード library(limma) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2), rep(3, param_G3))#G1群を1、G2群を2、G3群を3としたベクトルdata.clを作成 #本番(DEG検出) design <- model.matrix(~ 0 + as.factor(data.cl))#デザイン行列を作成した結果をdesignに格納 fit <- lmFit(data, design) #モデル構築 fit2 <- contrasts.fit(fit, contrasts=param_contrast)#コントラスト情報を与えている out <- eBayes(fit2) #検定(経験ベイズ) hoge <- topTable(out, n=nrow(data), sort.by="none")#解析結果を抽出してhogeに格納 p.value <- hoge$P.Value #p値をp.valueに格納 q.value <- hoge$adj.P.Val #q値をq.valueに格納 ranking <- rank(p.value) #p.valueでランキングした結果をrankingに格納 #ファイルに保存 tmp <- cbind(rownames(data), data, p.value, q.value, ranking)#入力データの右側にp.value、q.value、rankingを結合した結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
6. サンプルデータ25の10,000 genes×9 samplesのsample25.txtの場合:
「G1群 vs. G3群」の比較を行いたいときの指定方法(帰無仮説: G1 = G3)です。 出力ファイルのq.value列を眺めると、DEGに相当する最初の1-1000行目および2001-3000行目のところのほとんどのq.valueが0.1程度未満である一方、 G2群で高発現DEGの1001から2000行目のほとんどq.valueが比較的大きな数値となっていることから、param_contrastでの指定方法が妥当であることが分かります。 1-3.のようにparam_coefの枠組みではうまくG2 vs. G3をうまく表現できないので、コントラストという別の枠組みで指定しています。 思考回路としては、「a1*G1 + a2*G2 + a3*G3 = 0」として、この場合の目的である「G1 = G3という帰無仮説」を作成できるように、係数a1, a2, a3に適切な数値を代入することです。 ここではa1 = 1、a2 = 0, a3 = -1にすることで目的の帰無仮説を作成できます。 以下ではc(1, 0, -1)と指定していますが、 c(-1, 0, 1)でも構いません。理由はどちらでもG1 = G3を表現できているからです。
in_f <- "sample25.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge6.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 3 #G1群のサンプル数を指定 param_G2 <- 3 #G2群のサンプル数を指定 param_G3 <- 3 #G3群のサンプル数を指定 param_contrast <- c(1, 0, -1) #コントラスト情報を指定(reduced model作成用) #必要なパッケージをロード library(limma) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2), rep(3, param_G3))#G1群を1、G2群を2、G3群を3としたベクトルdata.clを作成 #本番(DEG検出) design <- model.matrix(~ 0 + as.factor(data.cl))#デザイン行列を作成した結果をdesignに格納 fit <- lmFit(data, design) #モデル構築 fit2 <- contrasts.fit(fit, contrasts=param_contrast)#コントラスト情報を与えている out <- eBayes(fit2) #検定(経験ベイズ) hoge <- topTable(out, n=nrow(data), sort.by="none")#解析結果を抽出してhogeに格納 p.value <- hoge$P.Value #p値をp.valueに格納 q.value <- hoge$adj.P.Val #q値をq.valueに格納 ranking <- rank(p.value) #p.valueでランキングした結果をrankingに格納 #ファイルに保存 tmp <- cbind(rownames(data), data, p.value, q.value, ranking)#入力データの右側にp.value、q.value、rankingを結合した結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
解析 | 発現変動 | 3群間 | 対応なし | 応用2 | limma (Smyth_2004)
limmaパッケージを用いて3群間比較用データで、 総当たりの2群間比較を一気に行うやり方を示します。 トランスクリプトーム解析本の4.2.2節の記述形式に準拠しています。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し、以下をコピペ
1. サンプルデータ24の31,099 probesets×10 samplesのdata_GSE30533_rma.txtの場合:
Affymetrix Rat Genome 230 2.0 Array (GPL1355)を用いて得られた、 2群間比較用のデータGSE30533 (Kamei et al., PLoS One, 2013)です。
オリジナルは「G1群5サンプル vs. G2群5サンプル」ですが、ここでは、「G1群4サンプル vs. G2群3サンプル vs. G3群3サンプル」とみなして、 全ての組合せ(G1vsG2, G1vsG3, and G2vsG3)の2群間比較を一気に行い、それらのp値(3列分)、q値(3列分)、および順位情報(3列分)を出力するやり方です。
in_f <- "data_GSE30533_rma.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge1.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 4 #G1群のサンプル数を指定 param_G2 <- 3 #G2群のサンプル数を指定 param_G3 <- 3 #G3群のサンプル数を指定 #必要なパッケージをロード library(limma) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み cl <- as.factor(c(rep("G1",param_G1), rep("G2",param_G2), rep("G3",param_G3)))#グループラベル情報をclに格納 #本番(DEG検出) design <- model.matrix(~ 0 + cl) #デザイン行列を作成した結果をdesignに格納 colnames(design) <- levels(cl) #デザイン行列の列名を付与 fit <- lmFit(data, design) #モデル構築(ばらつきの程度を見積もっている) contrast <- makeContrasts( #比較したい2群の情報を作成 G1vsG2 = G1 - G2, #比較したい2群の情報を作成 G1vsG3 = G1 - G3, #比較したい2群の情報を作成 G2vsG3 = G2 - G3, #比較したい2群の情報を作成 levels = design) #比較したい2群の情報を作成 fit2 <- contrasts.fit(fit, contrast) #モデル構築 out <- eBayes(fit2) #検定(経験ベイズ) p.value <- out$p.value #p値をp.valueに格納 q.value <- apply(p.value, MARGIN=2, p.adjust, method="BH")#q値をq.valueに格納 ranking <- apply(p.value, MARGIN=2, rank)#p.valueでランキングした結果をrankingに格納 #ファイルに保存 tmp <- cbind(rownames(data), data, p.value, q.value, ranking)#入力データの右側にp.value、q.value、rankingを結合した結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
2. サンプルデータ24の31,099 probesets×10 samplesのdata_GSE30533_rma.txtの場合:
Affymetrix Rat Genome 230 2.0 Array (GPL1355)を用いて得られた、 2群間比較用のデータGSE30533 (Kamei et al., PLoS One, 2013)です。
オリジナルは「G1群5サンプル vs. G2群5サンプル」ですが、ここでは、「G1群4サンプル vs. G2群3サンプル vs. G3群3サンプル」とみなして、 全ての組合せ(G1vsG2, G1vsG3, and G2vsG3)の2群間比較を一気に行い、それらのp値(3列分)、q値(3列分)、および順位情報(3列分)を出力するやり方です。
上記に加え、param_FDRで指定した閾値を満たす遺伝子数を数えあげ、重なり具合をベン図で描画しています。
in_f <- "data_GSE30533_rma.txt" #入力ファイル名を指定してin_fに格納 out_f1 <- "hoge2.txt" #出力ファイル名を指定してout_f1に格納 out_f2 <- "hoge2.png" #出力ファイル名を指定してout_f2に格納 param_G1 <- 4 #G1群のサンプル数を指定 param_G2 <- 3 #G2群のサンプル数を指定 param_G3 <- 3 #G3群のサンプル数を指定 param_fig <- c(600, 400) #ファイル出力時の横幅と縦幅を指定(単位はピクセル) param_FDR <- 0.20 #false discovery rate (FDR)閾値を指定 #必要なパッケージをロード library(limma) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み cl <- as.factor(c(rep("G1",param_G1), rep("G2",param_G2), rep("G3",param_G3)))#グループラベル情報をclに格納 #本番(DEG検出) design <- model.matrix(~ 0 + cl) #デザイン行列を作成した結果をdesignに格納 colnames(design) <- levels(cl) #デザイン行列の列名を付与 fit <- lmFit(data, design) #モデル構築(ばらつきの程度を見積もっている) contrast <- makeContrasts( #比較したい2群の情報を作成 G1vsG2 = G1 - G2, #比較したい2群の情報を作成 G1vsG3 = G1 - G3, #比較したい2群の情報を作成 G2vsG3 = G2 - G3, #比較したい2群の情報を作成 levels = design) #比較したい2群の情報を作成 fit2 <- contrasts.fit(fit, contrast) #モデル構築 out <- eBayes(fit2) #検定(経験ベイズ) p.value <- out$p.value #p値をp.valueに格納 q.value <- apply(p.value, MARGIN=2, p.adjust, method="BH")#q値をq.valueに格納 ranking <- apply(p.value, MARGIN=2, rank)#p.valueでランキングした結果をrankingに格納 #ファイルに保存(テキストファイル) tmp <- cbind(rownames(data), data, p.value, q.value, ranking)#入力データの右側にp.value、q.value、rankingを結合した結果をtmpに格納 write.table(tmp, out_f1, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存 #ファイルに保存(ベン図) png(out_f2, pointsize=13, width=param_fig[1], height=param_fig[2])#出力ファイルの各種パラメータを指定 vennDiagram(decideTests(out, adjust.method="BH", p.value=param_FDR))#ベン図を作成 dev.off() #おまじない
解析 | 発現変動 | 3群間 | 対応なし | 一元配置分散分析(One-way ANOVA)
一元配置分散分析(One-way ANOVA)を用いて、多群間での発現変動遺伝子の同定を行う。ここでは対応のない3群(G1, G2, G3群)の解析例を示しています。が、この解析結果を受けて「”どこかの群間で差がある”とされた遺伝子に対して、ではどの群間で発現に差があるのか?」を調べるpost-hoc test(ポストホック検定;)を行うのは大変そうですね。 ちなみに一元配置分散分析に対するポストホック検定として用いられるのは「Tukey検定(総当り比較の場合)」や「Dunnet検定(コントロール群のみとの比較の場合)」らしいです。 マイクロアレイの場合、普通は「”どこかの群間で差がある”として絞り込まれた遺伝子群」に対して行う”その後の解析”はクラスタリングだろうと思っていましたが、結構真面目にpost hoc testをやっている人もいますね。
例えばNorris et al., 2005では、ANOVA p-value < 0.01でoverall statistical testをやっておいて、その後の検定(post hoc test)としてScheffe's post hoc testでp-value < 0.05を満たす、という基準を用いています(Mougeot et al., 2006も同じ流れ)。 また、Wu et al., 2007では、ANOVA p-value < 0.05でoverall statistical testをやっておいて、その後の検定(post hoc test)としてTukey’s multiple comparison procedure を採用しています。 その後の解析でクラスタリングを行っている論文としてはYagil et al., 2005やPoulsen et al., 2005(これらは2-way ANOVAですが...)が挙げられます。
ここでは例題として用いた「G1群6サンプル、G2群5サンプル」の計11サンプルからなる対数変換(log2変換)後のファイル(sample2_log.txt)のラベル情報が「G1群3サンプル、G2群3サンプル、G3群5サンプル」になっていると仮定します:
「ファイル」−「ディレクトリの変更」で解析したいファイル(sample2_log.txt)を置いてあるディレクトリに移動し、以下をコピペ
1. やり方1:
in_f <- "sample2_log.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 3 #G1群のサンプル数を指定 param_G2 <- 3 #G2群のサンプル数を指定 param_G3 <- 5 #G3群のサンプル数を指定 #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2), rep(3, param_G3))#G1群を1、G2群を2、G3群を3としたベクトルdata.clを作成 #Oneway ANOVAを行い、F統計量とp値を返す関数Oneway_anovaを作成 Oneway_anova <- function(x, cl){ hoge <- oneway.test(x ~ cl, var=T) #Oneway ANOVA (一元配置分散分析)を行って、 return(c(hoge$statistic, hoge$p.value))#統計量とp値を結果として返す } #本番 out <- t(apply(data, 1, Oneway_anova, data.cl))#各(行)遺伝子についてOneway ANOVAを行った結果の統計量とp値をoutに格納 stat_f <- out[,1] #統計量をstat_fに格納 rank_f <- rank(-abs(stat_f)) #統計量の順位をrank_fに格納 p_f <- out[,2] #p値をp_fに格納 #ファイルに保存 tmp <- cbind(rownames(data), data, stat_f, p_f, rank_f)#入力データの右側に統計量、p値、その順位を結合した結果をtmpに格納。 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存 #以下は(こんなこともできますという)おまけ #Oneway ANOVA (一元配置分散分析)でp<0.05を満たす遺伝子群のみを抽出したい場合: param4 <- 0.05 #閾値を指定 out_f2 <- "hoge2.txt" #出力ファイル名を指定してout_fに格納 sum(p_f < param4) #条件を満たす遺伝子がいくつあったかを表示 tmp2 <- tmp[p_f < param4,] #条件を満たす遺伝子群の発現データをtmp2に格納 write.table(tmp2, out_f2, sep="\t", append=F, quote=F, row.names=F)#tmp2の中身を指定したファイル名で保存 #発現変動の度合いでソートした結果を得たい場合: out_f3 <- "hoge3.txt" #出力ファイル名を指定してout_fに格納 tmp2 <- tmp[order(rank_f),] #順位(rank_f)でソートした結果をtmp2に格納 write.table(tmp2, out_f3, sep="\t", append=F, quote=F, row.names=F)#tmp2の中身を指定したファイル名で保存
2. やり方2(関数の定義の部分が少し違うだけです):
in_f <- "sample2_log.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 3 #G1群のサンプル数を指定 param_G2 <- 3 #G2群のサンプル数を指定 param_G3 <- 5 #G3群のサンプル数を指定 #必要な関数などをロード source("http://www.iu.a.u-tokyo.ac.jp/~kadota/R/R_functions.R")#Oneway ANOVAを行い、F統計量とp値を返す関数Oneway_anova関数を含むファイルをあらかじめ読み込む #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2), rep(3, param_G3))#G1群を1、G2群を2、G3群を3としたベクトルdata.clを作成 #本番 out <- t(apply(data, 1, Oneway_anova, data.cl))#各(行)遺伝子についてOneway ANOVAを行った結果の統計量とp値をoutに格納 stat_f <- out[,1] #統計量をstat_fに格納 rank_f <- rank(-abs(stat_f)) #統計量の順位をrank_fに格納 p_f <- out[,2] #p値をp_fに格納 #ファイルに保存 tmp <- cbind(rownames(data), data, stat_f, p_f, rank_f)#入力データの右側に統計量、p値、その順位を結合した結果をtmpに格納。 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存 #以下は(こんなこともできますという)おまけ #Oneway ANOVA (一元配置分散分析)でp<0.05を満たす遺伝子群のみを抽出したい場合: param4 <- 0.05 #閾値を指定 out_f2 <- "hoge2.txt" #出力ファイル名を指定してout_fに格納 sum(p_f < param4) #条件を満たす遺伝子がいくつあったかを表示 tmp2 <- tmp[p_f < param4,] #条件を満たす遺伝子群の発現データをtmp2に格納 write.table(tmp2, out_f2, sep="\t", append=F, quote=F, row.names=F)#tmp2の中身を指定したファイル名で保存 #発現変動の度合いでソートした結果を得たい場合: out_f3 <- "hoge3.txt" #出力ファイル名を指定してout_fに格納 tmp2 <- tmp[order(rank_f),] #順位(rank_f)でソートした結果をtmp2に格納 write.table(tmp2, out_f3, sep="\t", append=F, quote=F, row.names=F)#tmp2の中身を指定したファイル名で保存
解析 | 発現変動 | 3群間 | 対応なし | Kruskal-Wallis(クラスカル-ウォリス)検定
Kruskal-Wallis (KW)検定を用いて、多群間での発現変動遺伝子の同定を行う。ここでは対応のない3群(G1, G2, G3群)の解析例を示しています。が、この解析結果を受けて「”どこかの群間で差がある”とされた遺伝子に対して、ではどの群間で発現に差があるのか?」を調べるpost-hoc test(ポストホック検定;)を行うのは大変そうですね。ちなみにKruskal-Wallis検定に対するポストホック検定として用いられるのは「Nemenyi検定」や「ボンフェローニ補正Mann-Whitney検定」らしいです。この方法はPubMedで調べても、実際にはほとんど使われていないようですね。ANOVAのほうは非常に頻繁に用いられるようですが...。
ここでは例題として用いた「G1群6サンプル、G2群5サンプル」の計11サンプルからなる対数変換(log2変換)後のファイル(sample2_log.txt)のラベル情報が「G1群3サンプル、G2群3サンプル、G3群5サンプル」になっていると仮定します:
「ファイル」−「ディレクトリの変更」で解析したいファイル(sample2_log.txt)を置いてあるディレクトリに移動し、以下をコピペ
1. やり方1:
in_f <- "sample2_log.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 3 #G1群のサンプル数を指定 param_G2 <- 3 #G2群のサンプル数を指定 param_G3 <- 5 #G3群のサンプル数を指定 #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2), rep(3, param_G3))#G1群を1、G2群を2、G3群を3としたベクトルdata.clを作成 #KW検定を行い、統計量とp値を返す関数Kruskal_wallisを作成。 Kruskal_wallis <- function(x, cl){ hoge <- kruskal.test(x ~ cl) #KW検定を行って、 return(c(hoge$statistic, hoge$p.value))#統計量とp値を結果として返す } #本番 out <- t(apply(data, 1, Kruskal_wallis, data.cl))#各(行)遺伝子についてKW検定検定を行った結果の統計量とp値をoutに格納 stat_kw <- out[,1] #統計量をstat_kwに格納 rank_kw <- rank(-abs(stat_kw)) #統計量の順位をrank_kwに格納 p_kw <- out[,2] #p値をp_kwに格納 #ファイルに保存 tmp <- cbind(rownames(data), data, stat_kw, p_kw, rank_kw)#入力データの右側に統計量、p値、その順位を結合した結果をtmpに格納。 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存 #以下は(こんなこともできますという)おまけ #KW検定でp<0.05を満たす遺伝子群のみを抽出したい場合: param4 <- 0.05 #閾値を指定 out_f2 <- "hoge2.txt" #出力ファイル名を指定してout_fに格納 sum(p_kw < param4) #条件を満たす遺伝子がいくつあったかを表示 tmp2 <- tmp[p_kw < param4,] #条件を満たす遺伝子群の発現データをtmp2に格納 write.table(tmp2, out_f2, sep="\t", append=F, quote=F, row.names=F)#tmp2の中身を指定したファイル名で保存 #発現変動の度合いでソートした結果を得たい場合: out_f3 <- "hoge3.txt" #出力ファイル名を指定してout_fに格納 tmp2 <- tmp[order(rank_kw),] #順位(rank_kw)でソートした結果をtmp2に格納 write.table(tmp2, out_f3, sep="\t", append=F, quote=F, row.names=F)#tmp2の中身を指定したファイル名で保存
2. やり方2(関数の定義の部分が少し違うだけです):
in_f <- "sample2_log.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 3 #G1群のサンプル数を指定 param_G2 <- 3 #G2群のサンプル数を指定 param_G3 <- 5 #G3群のサンプル数を指定 #必要な関数などをロード source("http://www.iu.a.u-tokyo.ac.jp/~kadota/R/R_functions.R")#KW検定を行い、統計量とp値を返す関数Kruskal_wallis関数を含むファイルをあらかじめ読み込む #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2), rep(3, param_G3))#G1群を1、G2群を2、G3群を3としたベクトルdata.clを作成 #本番 out <- t(apply(data, 1, Kruskal_wallis, data.cl))#各(行)遺伝子についてKW検定検定を行った結果の統計量とp値をoutに格納 stat_kw <- out[,1] #統計量をstat_kwに格納 rank_kw <- rank(-abs(stat_kw)) #統計量の順位をrank_kwに格納 p_kw <- out[,2] #p値をp_kwに格納 #ファイルに保存 tmp <- cbind(rownames(data), data, stat_kw, p_kw, rank_kw)#入力データの右側に統計量、p値、その順位を結合した結果をtmpに格納。 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存 #以下は(こんなこともできますという)おまけ #KW検定でp<0.05を満たす遺伝子群のみを抽出したい場合: param4 <- 0.05 #閾値を指定 out_f2 <- "hoge2.txt" #出力ファイル名を指定してout_fに格納 sum(p_kw < param4) #条件を満たす遺伝子がいくつあったかを表示 tmp2 <- tmp[p_kw < param4,] #条件を満たす遺伝子群の発現データをtmp2に格納 write.table(tmp2, out_f2, sep="\t", append=F, quote=F, row.names=F)#tmp2の中身を指定したファイル名で保存 #発現変動の度合いでソートした結果を得たい場合: out_f3 <- "hoge3.txt" #出力ファイル名を指定してout_fに格納 tmp2 <- tmp[order(rank_kw),] #順位(rank_kw)でソートした結果をtmp2に格納 write.table(tmp2, out_f3, sep="\t", append=F, quote=F, row.names=F)#tmp2の中身を指定したファイル名で保存
解析 | 発現変動 | 多群間 | について
手持ちのアレイデータが以下のような場合にこのカテゴリーに属す方法を適用します(色々な種類のサンプルが沢山ある場合):
サンプルA サンプルB サンプルC サンプルD サンプルE サンプルF サンプルG サンプルH サンプルI サンプルJ サンプルK サンプルL サンプルM ...
2013年6月に調査した結果をリストアップします。最近のものではBayesianIUTとSpeCondなどがR上で利用可能です。
- Dixon test:Greller and Tobin, Genome Res., 1999
- Pattern matching:Pavlidis and Noble, Genome Biol., 2001
- Ueda's AIC:Kadota et al., Physiol Genomics, 2003
- Tissue specificity index:Yanai et al., Bioinformatics, 2005
- Entropy:Schug et al., Genome Biol., 2005
- Sprent's non-parametric method:Ge et al., Genomics, 2005
- Tukey-Kramer’s HSD test:Liang et al., Physiol. Genomics, 2006
- ROKU:Kadota et al., BMC Bioinformatics, 2006
- BayesianIUT:Van Deun et al., Bioinformatics, 2009
- QDMR:Zhang et al., Nucleic Acids Res., 2011
- SpeCond:Cavalli et al., Genome Biol., 2011
- DSA:Zhong et al., BMC Bioinformatics, 2013
以下はROKU法に関する昔書いた記述です。
ROKUは二つの方法を組み合わせたものです。
- 「全体的な組織特異性の度合い」で遺伝子をランキング(エントロピーの低いものほどより組織特異的)
このとき、予めデータ変換したものに対してエントロピーを計算することで、組織特異的高発現だけでなく、 特異的低発現パターンなども検出可能という点でデータ変換せずにそのままエントロピーを計算するSchug's H(x) statisticよりも優れていることが>ROKU(Kadota et al., 2006)論文中で示されています。 - 「特異的なパターンを示す組織の検出」のために赤池情報量規準(AIC)に基づく方法で、特異的組織を外れ値として検出
単にエントロピーでランキングしただけでは、どこかの組織で特異的な遺伝子が上位にランキングされるだけで、どの組織で特異的なのかという情報は与えてくれません。そのために2番目の手順が必要になります。
ROKU論文中では単に「ここではAICに基づく方法を用いる」と書いており、同じ枠組みで結果を返す他の方法(Sprent's non-parametric method)が優れている可能性がROKU(Kadota et al., 2006)論文発表時にはまだ残されていました。
しかし、両者の比較解析論文(Kadota et al., 2007)で、「AICに基づく方法」が「Sprent's non-parametric method」よりも優れていることを結論づけています。
それゆえ→最初の文章に戻る
しかし、この方法にも欠点があります。
一つは「遺伝子ごとにROKU法によって得られたエントロピー値を計算してるが、全体のダイナミックレンジを考慮していない」です。
これは例えば10000genes×10samplesの遺伝子発現行列データがあったとして、その中の数値の最大値が23000, 最小値が1だったとします。
ある遺伝子の発現ベクトル(1,1,1,1,1,2,1,1,1,1)のエントロピーはROKU法では0となり、左から6番目の組織特異的高発現という判断が下され(てしまい)ますが、同じエントロピーが0の遺伝子ベクトルでも例えば(10000,5,5,5,5,5,5,5,5,5)のほうがより確からしいですよね。
もう一つは、ROKU法では、単にエントロピーの低い順にランキングするだけで、どの程度低ければいいのか?という指標は与えられていません...。
(組織特異的遺伝子検出を目的としたものではありませんが...)QDMR法 (Zhang et al., Nucleic Acids Res., 2011)という方法が最近提案されています。論文自体は、ゲノム中のサンプル間でDNAメチル化の程度が異なる領域(differentially methylated regions; DMRs)を定量化しようという試みの論文ですが、 regionをgeneと読み替えれば、組織特異的遺伝子検出法ROKUの改良版そのもの、ですよね?!
解析 | 発現変動 | 多群間 | SpeCond (Cavalli_2011)
SpeCondパッケージを用いて組織特異的発現遺伝子検出を行います。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し、以下をコピペ
1. ...の場合:
#必要なパッケージをロード library(SpeCond) #パッケージの読み込み
解析 | 発現変動 | 多群間 | ROKU (Kadota_2006)
TCCパッケージで提供しているROKU法(Kadota et al., 2006)を用いて、遺伝子発現行列中の遺伝子を全体的な組織特異性の度合いでランキングします。 出力ファイル中の"modH"列の数値は、「ROKU論文中のAdditional file 1(Suppl.xls)の"H(x')"列の数値」と対応しています。つまり、データ変換後のエントロピー値です。 "ranking"列は、modHの値でランキングした結果です。"ranking"列で昇順にソートすることで、全体的な組織特異性の度合いでランキングしていることになります。 つまり、上位が「(どの組織で特異的かはこのスコアだけでは分からないが)組織特異性が高い遺伝子」ということになります。 残りの結果は「1:特異的高発現、-1:特異的低発現、0:その他」からなる「外れ値行列」です。 例えば、組織AとBで1, それ以外の組織で0を示す遺伝子(群)は「AとB特異的高発現遺伝子」と判断します。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し、以下をコピペ
1. サンプルデータ21のsample21.txtの場合:
log2変換後のデータであるという前提です。
in_f <- "sample21.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge1.txt" #出力ファイル名を指定してout_fに格納 #必要なパッケージをロード library(TCC) #パッケージの読み込み #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 hoge <- ROKU(data) #ROKUを実行した結果をhogeに格納 outlier <- hoge$outlier #外れ値行列をoutlierに格納 modH <- hoge$modH #データ変換後のエントロピー値をmodHに格納(原著論文のH(x')の値に相当) ranking <- hoge$rank #modHでランキングした結果をrankingに格納 #ファイルに保存 tmp <- cbind(rownames(data), outlier, modH, ranking)#左端の列が遺伝子ID, 次にサンプル数分だけの列からなる「外れ値行列」、「modH」、「ranking」を結合してtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
2. サンプルデータ5のsample5.txtの場合:
おまけのところで、「心臓特異的発現パターン」を示す遺伝子群を抽出するための"理想的なパターン(テンプレート)"
を含むファイル(GDS1096_cl_heart.txt)を読み込んでいます。
in_f <- "sample5.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge2.txt" #出力ファイル名を指定してout_fに格納 #必要な関数などをロード source("http://www.iu.a.u-tokyo.ac.jp/~kadota/R/R_functions.R")#ROKUを実行するkadota_2006_bmc_bioinformatics関数を含むファイルをあらかじめ読み込む library(affy) #Tukey's Biweightを計算するためのtukey.biweight関数が含まれているパッケージの読み込み library(som) #各遺伝子発現ベクトルを正規化(平均=0, 標準偏差=1)するためのnormalize関数が含まれているパッケージの読み込み #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 data.z <- normalize(data, byrow=TRUE) #正規化を実行し、結果をdata.zに格納 out <- t(apply(data.z, 1, kadota_2003_physiol_genomics_0.25))#各遺伝子発現ベクトルについて、Ueda's AIC-based methodを適用し、「特異的高発現=1, 低発現=-1, それ以外=0」の三状態の結果を返す colnames(out) <- colnames(data) #列名を付与 entropy_score <- apply(data, 1, kadota_2006_bmc_bioinformatics)#一行(一遺伝子)づつ、遺伝子発現ベクトルxを変換(x' = |x - Tbw|> )してからエントロピーH(x')を計算し、entropy_scoreに格納 #ファイルに保存 tmp <- cbind(rownames(data), out, entropy_score)#左端の列が遺伝子ID, 次にサンプル数分だけの列からなる「外れ値行列情報」、そして最後の列にエントロピー値H(x')からなる行列としてtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存 #以下は(こんなこともできますという)おまけ #心臓特異的高発現遺伝子群のみのサブセットをentropy_scoreの低い順に得たい場合: in_f2 <- "GDS1096_cl_heart.txt" #入力ファイル名2(心臓で1、それ以外で0のテンプレートパターンファイル)を指定 out_f2 <- "hoge2.txt" #出力ファイル名を指定してout_fに格納 library(genefilter) #似た発現パターンを示す遺伝子をランキングするためのgenefinder関数が含まれているパッケージの読み込み data_cl <- read.table(in_f2, sep="\t", quote="")#入力ファイル2を読み込んでdata_clに格納 template <- data_cl[,2] #バイナリ(0 or 1)情報(2列目)のみ抽出し、templateに格納 tmp <- rbind(out, template) #templateというテンプレートパターンを得られたはずれ値行列outの最後の行に追加した結果をtmpに格納 closeg <- genefinder(tmp, nrow(out)+1, nrow(out))#特異的発現の度合いでランキングされた結果をclosegに格納 obj <- closeg[[1]]$indices[closeg[[1]]$dists == 0]#テンプレートと完全に同じ遺伝子の行番号情報をobjに格納 length(obj) #目的の特異的発現遺伝子がいくつあったかを表示 tmp <- cbind(rownames(data), data, entropy_score)#入力データの右側にエントロピー値H(x')を結合した結果をtmpに格納 tmp2 <- tmp[obj,] #行列tmpの中からobjで示された行番号に相当する行のみ抽出してtmp2に格納 tmp3 <- tmp2[order(tmp2$entropy_score),]#目的の特異的発現遺伝子群をエントロピーの低い順にソートしてtmp3に格納 write.table(tmp3, out_f2, sep="\t", append=F, quote=F, row.names=F)#tmp3の中身を指定したファイル名で保存 #全遺伝子をentropy_scoreの低い順にソートした結果を得たい場合: out_f3 <- "hoge3.txt" #出力ファイル名を指定してout_f3に格納 tmp <- cbind(rownames(data), out, entropy_score)#左端の列が遺伝子ID, 次にサンプル数分だけの列からなる「外れ値行列情報」、そして最後の列にエントロピー値H(x')からなる行列としてtmpに格納 tmp2 <- tmp[order(entropy_score),] #順位(entropy_score)でソートした結果をtmp2に格納 write.table(tmp2, out_f3, sep="\t", append=F, quote=F, row.names=F)#tmp2の中身を指定したファイル名で保存
おまけまでやって得られるhoge2.txtをエクセルなどで開くと、心臓特異的高発現遺伝子が231個検出されていることがわかります。ここまで(231個のうちのどれが一番特異的な遺伝子かなどはわからないということ)しかできなかったのがUeda's AIC-based methodですが、ROKUではエントロピーH(x')も計算するので、得られたサブセット内のランキング(hoge.txt中の“最後の列”H(x')の低い順にソート)が可能になりました。
解析 | 発現変動 | 多群間 | Sprent's non-parametric method
Ge et al., Genomics, 86(2), 127-141, 2005で用いられた方法です。一つ一つの遺伝子の発現パターン(遺伝子発現ベクトルx)に対して、特異的高(and/or 低)発現組織の有無を一意的に返してくれるという点でUeda's AIC-based methodと同じです。ちなみにこの方法よりもUeda's AIC-based methodのほうが優れていることが参考文献1で示されています。
やっていることは非常にシンプルで、
- 各遺伝子発現ベクトルを独立に中央値を=0、MAD=1になるようにスケーリング
- データ変換後の値の絶対値がXより大きい組織を"特異的組織"とする
を行っているだけです。
ちなみにこのやり方を採用した原著論文(Ge et al., Genomics, 2005)ではX=5としているので、ここではX=5とした場合の解析例を示します。
以下を実行して得られるファイル(hoge.txt)中の結果は「1:特異的高発現、-1:特異的低発現、0:その他」からなる「外れ値行列」なので、
例えば、組織A and Bで1, それ以外の組織で0を示す遺伝子(群)は「AとB特異的高発現遺伝子」ということになります。
「ファイル」−「ディレクトリの変更」で解析したいファイル(遺伝子発現データ:sample5.txt、テンプレートパターン:GDS1096_cl_heart.txt)を置いてあるディレクトリに移動し、以下をコピペ
1. ...の場合:
in_f <- "sample5.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge.txt" #出力ファイル名を指定してout_fに格納 param1 <- 5 #Xの値を指定 #データファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 data.t <- t(data) #行列の転置(この後に使うscale関数が列ごとの操作を行うため、scale関数をそのまま使えるように予め行列を入れ替えておく必要があるため) data.t.m.mad <- scale(data.t, apply(data.t, 2, median), apply(data.t, 2, mad, constant=1))#各列のmedian=0, MAD=1になるようにスケーリングし、結果をdata.t.m.madに格納 data.m.mad <- t(data.t.m.mad) #scale関数の適用が終わったので、もう一度行列の転置を行って元に戻し、結果をdata.m.madに格納 out <- data.m.mad #out.m.madをoutにコピー out[(out <= param1) & (out >= -param1)] <- 0#スケーリング後の値で"-param1"以上"param1"以下の値を0に置換 out[out < -param1] <- -1 #スケーリング後の値で-param1未満の値を-1に置換 out[out > param1] <- 1 #スケーリング後の値でparam1より大きい値を1に置換 colnames(out) <- colnames(data) #列名を付与 #ファイルに保存 tmp <- cbind(rownames(data), out) #遺伝子IDの右側に, サンプル数分だけの「外れ値行列」を結合した結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存 #以下は(こんなこともできますという)おまけ #心臓特異的高発現遺伝子群のみのサブセットを得たい場合: in_f2 <- "GDS1096_cl_heart.txt" #入力ファイル名2(心臓で1、それ以外で0のテンプレートパターンファイル)を指定 out_f2 <- "hoge2.txt" #出力ファイル名を指定してout_f2に格納 library(genefilter) #似た発現パターンを示す遺伝子をランキングするためのgenefinder関数が含まれているパッケージの読み込み data_cl <- read.table(in_f2, sep="\t", quote="")#入力ファイル2を読み込んでdata_clに格納 template <- data_cl[,2] #バイナリ(0 or 1)情報(2列目)のみ抽出し、templateに格納 tmp <- rbind(out, template) #templateというテンプレートパターンを得られたはずれ値行列outの最後の行に追加した結果をtmpに格納 closeg <- genefinder(tmp, nrow(out)+1, nrow(out))#特異的発現の度合いでランキングされた結果をclosegに格納 obj <- closeg[[1]]$indices[closeg[[1]]$dists == 0]#テンプレートと完全に同じ遺伝子の行番号情報をobjに格納 length(obj) #目的の特異的発現遺伝子がいくつあったかを表示 tmp <- cbind(rownames(data[obj,]), data[obj,])#dataの中からobjで示された行番号に相当する行のみの遺伝子IDと発現データを結合してtmpに格納 write.table(tmp, out_f2, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
解析 | 発現変動 | 多群間 | Schug's H(x) statistic
一つ一つの遺伝子の発現パターン(遺伝子発現ベクトルx)に対して、そのエントロピーH(x)を計算します。エントロピーが低い(最小値は0)ほど、その遺伝子の組織特異性の度合いが高いことを意味します。また逆に、エントロピーが高い(最大値はlog2(組織数); 例えば解析組織数が16の場合はlog2(16)=4が最大値となる)ほど、その遺伝子の組織特異性の度合いが低いことを意味します。
したがって、ここでは各遺伝子についてエントロピーH(x)を計算したのち、H(x)で昇順にソートした結果を出力するところまで行います。但し、エントロピーが低いからといって、どの組織で特異的発現を示すかまでは教えてくれないという弱点があるため、目的組織を指定することは原理的(数式的)に不可能です。
使い方としては、様々な実験条件のデータが手元にあった場合などで、「どの条件でもいいから特異的な発現パターンを示す遺伝子を上位からソートしたい」ような場合に使えますが、この方法の改良版ROKUのほうが、“組織特異的低発現パターンなど様々な特異的発現パターンを統一的にランキング可能である”という点において理論的にも実際上も優れているので、この目的においてはROKUを利用することをお勧めします。
「ファイル」−「ディレクトリの変更」で解析したい遺伝子発現行列のファイルを置いてあるディレクトリに移動し、以下をコピペ
1. 入力ファイルがsample5.txtの場合:
in_f <- "sample5.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge.txt" #出力ファイル名を指定してout_fに格納 #必要な関数などをロード source("http://www.iu.a.u-tokyo.ac.jp/~kadota/R/R_functions.R")#エントロピーを計算するshannon.entropy関数を含むファイルをあらかじめ読み込む #データファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 entropy_score <- apply(data, 1, shannon.entropy)#エントロピーを計算した結果をentropy_scoreに格納 #ファイルに保存 tmp <- cbind(rownames(data), data, entropy_score)#入力データの右側に計算したentropy_scoreを結合した結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存 #以下は(こんなこともできますという)おまけ #全遺伝子をentropy_scoreの低い順にソートした結果を得たい場合: out_f2 <- "hoge2.txt" #出力ファイル名を指定してout_f2に格納 tmp2 <- tmp[order(entropy_score),] #順位(entropy_score)でソートした結果をtmp2に格納 write.table(tmp2, out_f2, sep="\t", append=F, quote=F, row.names=F)#tmp2の中身を指定したファイル名で保存
2. 入力ファイルがsample15.txtの場合:
in_f <- "sample15.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge.txt" #出力ファイル名を指定してout_fに格納 #必要な関数などをロード source("http://www.iu.a.u-tokyo.ac.jp/~kadota/R/R_functions.R")#エントロピーを計算するshannon.entropy関数を含むファイルをあらかじめ読み込む #データファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 entropy_score <- apply(data, 1, shannon.entropy)#エントロピーを計算した結果をentropy_scoreに格納 #ファイルに保存 tmp <- cbind(rownames(data), data, entropy_score)#入力データの右側に計算したentropy_scoreを結合した結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存 #以下は(こんなこともできますという)おまけ #全遺伝子をentropy_scoreの低い順にソートした結果を得たい場合: out_f2 <- "hoge2.txt" #出力ファイル名を指定してout_fに格納 tmp2 <- tmp[order(entropy_score),] #順位(entropy_score)でソートした結果をtmp2に格納 write.table(tmp2, out_f2, sep="\t", append=F, quote=F, row.names=F)#tmp2の中身を指定したファイル名で保存
解析 | 発現変動 | 多群間 | Schug's Q statistic
Schugらの方法(Entropy-based Q-statistic)を用いて、任意の1組織(と他の少数の組織)で特異的に発現している遺伝子をランキングします。Schug's H(x) statisticの方法は「どの組織で特異的発現を示すかまでは教えてくれない」という弱点がありました。その1つの解決策としてSchugらが提案している「指定した目的組織(と他の少数の組織)」で特異的な発現パターンを示す遺伝子を上位からランキングする統計量Qを計算します。
最終的に得られるhoge.txtファイルをエクセルなどで開いて、目的組織に相当するカラムでQ-statisticを昇順にソートすれば、目的組織特異的遺伝子をランキングすることができます。
しかし、この方法は目的組織以外の組織でも発現しているようなパターンが上位に来てしまう場合があるという弱点があります。この弱点を改善した方法がROKUです。
「ファイル」−「ディレクトリの変更」で解析したい遺伝子発現行列のファイル(sample5.txt)を置いてあるディレクトリに移動し、以下をコピペ
1. 入力ファイルがsample5.txtの場合:
in_f <- "sample5.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge.txt" #出力ファイル名を指定してout_fに格納 #必要な関数などをロード source("http://www.iu.a.u-tokyo.ac.jp/~kadota/R/R_functions.R")#Schug's Q statisticを計算するshannon.entropy.q関数を含むファイルをあらかじめ読み込む #データファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 entropy_score <- apply(data, 1, shannon.entropy)#エントロピーを計算した結果をentropy_scoreに格納 q_score <- t(apply(data, 1, shannon.entropy.q))#Schug's Q statisticを計算した結果をq_scoreに格納 #ファイルに保存 tmp <- cbind(rownames(data), q_score, entropy_score)#遺伝子IDの右側に計算したQスコアの行列とentropy_scoreを結合した結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存 #以下は(こんなこともできますという)おまけ #入力データの左からX番目の組織について特異性の度合いの高い順(その列のQスコアの低い順)にソートした結果を得たい場合: #(X=2の場合は"Amygdala"に相当します) out_f2 <- "hoge2.txt" #出力ファイル名を指定してout_f2に格納 param1 <- 2 #Xの値を指定 tmp2 <- tmp[order(q_score[,param1]),] #行列q_scoreを"param1"列でソートした結果をtmp2に格納 write.table(tmp2, out_f2, sep="\t", append=F, quote=F, row.names=F)#tmp2の中身を指定したファイル名で保存
解析 | 発現変動 | 多群間 | Ueda's AIC-based method
Kadota et al., Physiol. Genomics, 12(3), 251-259, 2003で提案された方法です。一つ一つの遺伝子の発現パターン(遺伝子発現ベクトルx)に対して、特異的高(and/or 低)発現組織の有無を一意的に返してくれます。この方法は、ROKUの要素技術として使われており、実際の解析にはROKUの利用をお勧めします。尚、用いている関数("kadota_2003_physiol_genomics_0.50" for Ueda's AIC-based method; "kadota_2003_physiol_genomics_0.25" for ROKU)が両者で微妙に違いますが、これは論文との整合性(Kadota et al., Physiol. Genomics, 12(3), 251-259, 2003論文中では探索する最大外れ値候補数を全サンプル数の50%に設定;ROKU(Kadota et al., BMC Bioinformatics, 7, 294, 2006)論文中では25%に設定)をとっているためです。
競合する方法にSprent's non-parametric methodがありますが、それよりも優れていることが参考文献1で示されています。
以下を実行して得られるファイル(hoge.txt)中の結果は「1:特異的高発現、-1:特異的低発現、0:その他」からなる「外れ値行列」なので、
例えば、組織A and Bで1, それ以外の組織で0を示す遺伝子(群)は「AとB特異的高発現遺伝子」ということになります。
「ファイル」−「ディレクトリの変更」で解析したいファイル(遺伝子発現データ:sample5.txt、テンプレートパターン:GDS1096_cl_heart.txt)を置いてあるディレクトリに移動し、以下をコピペ
1. 入力ファイルがsample5.txtの場合:
in_f <- "sample5.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge.txt" #出力ファイル名を指定してout_fに格納 #必要な関数などをロード source("http://www.iu.a.u-tokyo.ac.jp/~kadota/R/R_functions.R")#Ueda's AIC-based methodを実行するkadota_2003_physiol_genomics_0.50関数を含むファイルをあらかじめ読み込む library(som) #各遺伝子発現ベクトルを正規化(平均=0, 標準偏差=1)するためのnormalize関数が含まれているパッケージの読み込み #データファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 data.z <- normalize(data, byrow=TRUE) #正規化を実行し、結果をdata.zに格納 out <- t(apply(data.z, 1, kadota_2003_physiol_genomics_0.50))#各遺伝子発現ベクトルについて、Ueda's AIC-based methodを適用し、「特異的高発現=1, 低発現=-1, それ以外=0」の三状態の結果を返す colnames(out) <- colnames(data) #列名を付与 #ファイルに保存 tmp <- cbind(rownames(data), out) #左端の列が遺伝子IDとサンプル数分だけの列からなる「外れ値行列」を結合してtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存 #以下は(こんなこともできますという)おまけ #心臓特異的高発現遺伝子群のみのサブセットを得たい場合: in_f2 <- "GDS1096_cl_heart.txt" #入力ファイル名2(心臓で1、それ以外で0のテンプレートパターンファイル)を指定 out_f2 <- "hoge2.txt" #出力ファイル名を指定してout_f2に格納 library(genefilter) #似た発現パターンを示す遺伝子をランキングするためのgenefinder関数が含まれているパッケージの読み込み data_cl <- read.table(in_f2, sep="\t", quote="")#入力ファイル2を読み込んでdata_clに格納 template <- data_cl[,2] #バイナリ(0 or 1)情報(2列目)のみ抽出し、templateに格納 tmp <- rbind(out, template) #templateというテンプレートパターンを得られたはずれ値行列outの最後の行に追加した結果をtmpに格納 closeg <- genefinder(tmp, nrow(out)+1, nrow(out))#特異的発現の度合いでランキングされた結果をclosegに格納 obj <- closeg[[1]]$indices[closeg[[1]]$dists == 0]#テンプレートと完全に同じ遺伝子の行番号情報をobjに格納 length(obj) #目的の特異的発現遺伝子がいくつあったかを表示 tmp <- cbind(rownames(data[obj,]), data[obj,])#dataの中からobjで示された行番号に相当する行のみの遺伝子IDと発現データを結合してtmpに格納 write.table(tmp, out_f2, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
解析 | 発現変動 | 多群間 | パターンマッチング法(テンプレートマッチング法)
(基本的には、解析 | 似た発現パターンを持つ遺伝子の同定をご覧ください。)
パターンマッチング法を用いて、指定した理想的なパターンとの類似度が高い遺伝子の同定を行うやり方を紹介します。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し、以下をコピペ
1. サンプルデータのsample15.txtとテンプレートパターンファイル(sample15_cl.txt)を用いる場合(基本形):
in_f1 <- "sample15.txt" #入力ファイル名(発現データ)を指定してin_f1に格納 in_f2 <- "sample15_cl.txt" #入力ファイル名(テンプレート情報)を指定してin_f2に格納 out_f <- "hoge1.txt" #出力ファイル名を指定してout_fに格納 #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f1, header=TRUE, row.names=1, sep="\t", quote="")#in_f1で指定したファイルの読み込み hoge <- read.table(in_f2, sep="\t", quote="")#in_f2で指定したファイルの読み込み data.cl <- hoge[,2] #テンプレートパターンベクトルdata.clを作成 #本番 r <- apply(data, 1, cor, y=data.cl) #各(行)遺伝子についてテンプレートパターンdata.clとの相関係数を計算した結果をrに格納 #ファイルに保存 tmp <- cbind(rownames(data), data, r) #入力データの右側に相関係数rのベクトルを結合した結果をtmpに格納。 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
2. 相関係数の高い順(降順)にソートしたい場合:
in_f1 <- "sample15.txt" #入力ファイル名(発現データ)を指定してin_f1に格納 in_f2 <- "sample15_cl.txt" #入力ファイル名(テンプレート情報)を指定してin_f2に格納 out_f <- "hoge2.txt" #出力ファイル名を指定してout_fに格納 #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f1, header=TRUE, row.names=1, sep="\t", quote="")#in_f1で指定したファイルの読み込み hoge <- read.table(in_f2, sep="\t", quote="")#in_f2で指定したファイルの読み込み data.cl <- hoge[,2] #テンプレートパターンベクトルdata.clを作成 #本番 r <- apply(data, 1, cor, y=data.cl) #各(行)遺伝子についてテンプレートパターンdata.clとの相関係数を計算した結果をrに格納 #ファイルに保存 tmp <- cbind(rownames(data), data, r) #入力データの右側に相関係数rのベクトルを結合した結果をtmpに格納。tmp2 <- tmp[order(r, decreasing=TRUE),]#相関係数で降順にソート結果をtmp2に格納。 write.table(tmp2, out_f, sep="\t", append=F, quote=F, row.names=F)#tmp2の中身を指定したファイル名で保存
3. 相関係数の低い順(昇順)にソートしたい場合:
in_f1 <- "sample15.txt" #入力ファイル名(発現データ)を指定してin_f1に格納 in_f2 <- "sample15_cl.txt" #入力ファイル名(テンプレート情報)を指定してin_f2に格納 out_f <- "hoge3.txt" #出力ファイル名を指定してout_fに格納 #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f1, header=TRUE, row.names=1, sep="\t", quote="")#in_f1で指定したファイルの読み込み hoge <- read.table(in_f2, sep="\t", quote="")#in_f2で指定したファイルの読み込み data.cl <- hoge[,2] #テンプレートパターンベクトルdata.clを作成 #本番 r <- apply(data, 1, cor, y=data.cl) #各(行)遺伝子についてテンプレートパターンdata.clとの相関係数を計算した結果をrに格納 #ファイルに保存 tmp <- cbind(rownames(data), data, r) #入力データの右側に相関係数rのベクトルを結合した結果をtmpに格納。tmp2 <- tmp[order(r, decreasing=FALSE),]#相関係数で昇順にソート結果をtmp2に格納。 write.table(tmp2, out_f, sep="\t", append=F, quote=F, row.names=F)#tmp2の中身を指定したファイル名で保存
解析 | 発現変動 | 時系列 | について
手持ちのアレイデータが以下のような場合には「non-periodic genes」のカテゴリーに属す方法を適用し(いわゆる「経時変化遺伝子」を検出したいとき)、 24時間周期のような周期的に発現変動する遺伝子(circadian gene)を検出することが目的の場合には「Periodic genes」のカテゴリーに属す方法を適用します。
サンプルAの刺激後 0Hのデータ サンプルAの刺激後 1Hのデータ サンプルAの刺激後 6Hのデータ サンプルAの刺激後24Hのデータ
2013年6月に調査した結果をリストアップします。Rで利用可能なのはGeneCycle, EMMIX-WIRE。
Periodic gene検出用
- Wichert's method (GeneCycleパッケージ):Wichert et al., Bioinformatics, 2004
- A model-based method:Luan and Li, Bioinformatics, 2004
- Fourier-score-based algorithm:de Lichtenberg et al, Bioinformatics, 2005
- Ahdesmaki's method (GeneCycleパッケージ):Ahdesmaki et al., BMC Bioinformatics, 2005
- Lomb-Scargle periodgram:Glynn et al., Bioinformatics, 2006
- C&G procedure:Chen J., BMC Bioinformatics, 2005
- Liew's method:Liew et al., BMC Bioinformatics, 2007
- M-estimator(GeneCycleパッケージ):Ahdesmaki et al., BMC Bioinformatics, 2007
- Laplace periodogram(MATLAB; リンク切れ):Liang and Wang, BMC Bioinformatics, 2009
- An empirical Bayes procedure (MATLAB):Chudova et al., Bioinformatics, 2009
- A permutation-based method (リンク切れ):Sohn et al., BMC Bioinformatics, 2009
- ARSER(BioClockというweb serverでも利用可能):Yang and Su, Bioinformatics, 2010
- SCM:Junier et al., Algorithms Mol. Biol., 2010
- LSPR(MATLAB; BioClockというweb serverでも利用可能):Yang et al., Bioinformatics, 2011
- Principal-oscillation-pattern:Wang et al., PLoS One, 2012
- EMMIX-WIRE(著者にメール):Wang et al., BMC Bioinformatics, 2012
- FPCA:Wu and Wu, BMC Bioinformatics, 2013
Non-periodic gene検出用
- samr:Tusher et al., PNAS, 2001
- maSigPro:Conesa et al., Bioinformatics, 2006
- ICA:Frigyesi et al., BMC Bioinformatics, 2006
- Ahnert's method:Ahnert et al., Bioinformatics, 2006
- Di Camillo's method:Di Camillo et al., BMC Bioinformatics, 2007
- TimeClust:Magni et al., Bioinformatics, 2008
- BATS (英語じゃないので何を書いてるのか不明...):Angelini et al., BMC Bioinformatics, 2008
- betr:Aryee et al., BMC Bioinformatics, 2009
- SEA (web tool):Nueda et al., Nucleic Acids Res., 2010
- PESTS (web tool):Sinha and Markatou, BMC Bioinformatics, 2011
- Gaussian processes (gptkパッケージ):Kalaitzis and Lawrence, BMC Bioinformatics, 2011
- BHC:Cooke et al., BMC Bioinformatics, 2011
- IPCA (mixOmicsパッケージ):Yao et al., BMC Bioinformatics, 2012
- Di Camillo's method:Di Camillo et al., PLoS One, 2012
- randomized BHC:Darkins et al., PLoS One, 2013
解析 | 発現変動 | 時系列 | Periodic genes | M-estimator (Ahdesmaki_2007)
参考文献1, 2の方法を実装したものです。
「ファイル」−「ディレクトリの変更」で解析したいファイル(sample12.txt)を置いてあるディレクトリに移動し、以下をコピペ
1. サンプルデータのsample12.txtの場合:
「0, 15, 30, 45, 60, 75, 90, 105, 120, 135, 150minの計11 time points×1,444 genes (ORFs)からなる時系列データです。
in_f <- "sample12.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge1.txt" #出力ファイル名を指定してout_fに格納 #必要なパッケージをロード library(GeneCycle) #パッケージの読み込み #データファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #本番 out1 <- avgp(t(data)) #平均のピリオドグラムを計算し周波数(frequency)成分ごとの平均パワースペクトル密度(average power spectral density)の結果をout1に格納 out2 <- t(dominant.freqs(t(data),3)) #dominantな周波数(frequency)成分の上位3つをout2に格納 tmp_p <- fisher.g.test(t(data)) #Fisher’s Exact g Testを行って得たp値をtmp_pに格納 tmp_fdr <- fdrtool(tmp_p, statistic="pvalue")#False Discovery Rate (FDR)を計算した結果をtmp_fdrに格納 tmp_robust_p <- robust.g.test(robust.spectrum(t(data)))#Fisher’s Exact g Testのa robust nonparametric versionでp値を計算した結果をtmp_robust_pに格納 p_gc <- tmp_fdr$pval #p値をp_gcに格納 lfdr_gc <- tmp_fdr$lfdr #local FDR値をlfdr_gcに格納 #ファイルに保存 tmp <- cbind(rownames(data), data, p_gc, lfdr_gc)#入力データの右側にp値、local FDRを結合した結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存 #以下は(こんなこともできますという)おまけ #(local)FDRがX未満(たとえば0.1を指定するとこの閾値を満たす遺伝子数のうち本当は発現変動遺伝子でないものが含まれる割合を0.1)の遺伝子数を表示したい場合: param_FDR <- 0.1 #false discovery rate (FDR)閾値を指定 sum(fdr_gc$lfdr < param_FDR) #条件を満たす遺伝子数を表示 #平均のピリオドグラムを得たい場合: avgp(t(data)) #平均のピリオドグラムを計算し周波数(frequency)成分ごとの平均パワースペクトル密度(average power spectral density)の結果をout1に格納 #dominantな周波数(frequency)成分の上位3つを得たい場合: out2 <- t(dominant.freqs(t(data),3)) #dominantな周波数(frequency)成分の上位3つをout2に格納 dim(out2) #out2の行数と列数を表示(1441遺伝子の一つにつき上位3つの周波数成分が格納されているので1441行3列になる)
解析 | 発現変動 | 時系列 | Periodic genes | Lomb-Scargle periodogram (Glynn_2006)
周期性解析によく用いられる方法としてはFast Fourier Transform (FFT) アルゴリズムがありますが、この方法は1) time-pointの間隔が等しくなければいけない, 2) 欠損値があってはいけない、という制約がありました。
Lomb-Scargle periodogram(Glynn et al., Bioinformatics, 2006)を用いることで上記2つの条件を満たさない場合でもうまく取り扱ってくれるようです。もちろん、False Discovery Rate (FDR)をコントロールして有意なperiodicな発現パターンを検出してくれます。
- LombScargle.zipファイルをデスクトップにダウンロード
- R上ではなく(つまり、「パッケージ」-「ローカルにあるzipファイルからのパッケージのインストール」ではない!!ということ)、普通にLombScargle.zipファイルを解凍
- Step-by-Step Instructionsを参考にしながら、自分の時系列データを解析
解析 | 発現変動 | 時系列 | non-periodic genes | randomized BHC (Darkins_2013)
BHCパッケージで利用可能なrandomized BHC法を用いて時系列データの中から統計的に有意な発現の異なるプロファイルを検出します。
「ファイル」−「ディレクトリの変更」で解析したい時系列遺伝子発現データのファイルとその実験デザイン情報に関するファイルを置いてあるディレクトリに移動し、以下をコピペ
#必要なパッケージをロード library(BHC) #パッケージの読み込み
解析 | 発現変動 | 時系列 | non-periodic genes | IPCA (Yao_2012)
mixOmicsパッケージで利用可能なIPCA法を用いて時系列データの中から統計的に有意な発現の異なるプロファイルを検出します。
「ファイル」−「ディレクトリの変更」で解析したい時系列遺伝子発現データのファイルとその実験デザイン情報に関するファイルを置いてあるディレクトリに移動し、以下をコピペ
#必要なパッケージをロード library(mixOmics) #パッケージの読み込み
解析 | 発現変動 | 時系列 | non-periodic genes | gptk (Kalaitzis_2011)
gptkパッケージを用いて時系列データの中から統計的に有意な発現の異なるプロファイルを検出します。
「ファイル」−「ディレクトリの変更」で解析したい時系列遺伝子発現データのファイルとその実験デザイン情報に関するファイルを置いてあるディレクトリに移動し、以下をコピペ
#必要なパッケージをロード library(gptk) #パッケージの読み込み
解析 | 発現変動 | 時系列 | non-periodic genes | betr (Aryee_2009)
betrパッケージを用いて時系列データの中から統計的に有意な発現の異なるプロファイルを検出します。
「ファイル」−「ディレクトリの変更」で解析したい時系列遺伝子発現データのファイルとその実験デザイン情報に関するファイルを置いてあるディレクトリに移動し、以下をコピペ
#必要なパッケージをロード library(betr) #パッケージの読み込み
解析 | 発現変動 | 時系列 | non-periodic genes | maSigPro (Conesa_2006)
maSigPro(Conesa et al., 2006)パッケージを用いて時系列データの中から統計的に有意な発現の異なるプロファイルを検出します。
サンプルデータで示すような「あるサンプル(A)に刺激を与えて3h, 9h, and 27h後に測定した時系列データ」が手元にあり、 「経時的に発現の異なる遺伝子」を検出したい場合に行います。 ここではFDR("発現変動している"としたもののうち"本当は発現変動していない"ものが含まれる割合; 0 < FDR <= 1)を0.5として計算した結果を示してありますが、 その閾値を満たす遺伝子数があまりにも少なくて困るような場合には最大で1.0まで設定することが可能です。もちろん最初からFDRを1.0に設定しておいて、(解析可能な)全遺伝子の結 果を眺めるという戦略でもいいと思います。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し、以下をコピペ
1. サンプルデータのsample10_1group.txtとその実験デザインファイル(sample10_1group_cl.txt)の場合:
in_f1 <- "sample10_1group.txt" #入力ファイル名(発現データファイル)を指定してin_f1に格納 in_f2 <- "sample10_1group_cl.txt" #入力ファイル名(実験デザインファイル)を指定してin_f2に格納 out_f <- "hoge1.txt" #出力ファイル名を指定してout_fに格納 param_FDR <- 0.5 #false discovery rate (FDR)閾値を指定 #必要なパッケージをロード library(maSigPro) #パッケージの読み込み #データファイルの読み込み data <- read.table(in_f1, header=TRUE, row.names=1, sep="\t", quote="")#in_f1で指定したファイルの読み込み edesign <- read.table(in_f2, header=TRUE, row.names=1, sep="\t", quote="")#in_f2で指定したファイルの読み込み #本番 design <- make.design.matrix(edesign, degree=2)#実験デザイン行列の作成。degree=2は、2次の回帰モデルで考えることを意味する fit <- p.vector(data, design, Q=param_FDR)#回帰モデルの作成/span> tstep <- T.fit(fit) #得られた発現変動遺伝子群の各々について最もよい回帰モデルを決める gene_profile <- tstep$sig.profiles #発現変動遺伝子の発現プロファイルをgene_profileに格納。 gene_id <- rownames(gene_profile) #発現変動遺伝子のIDをgene_idに格納。 p.value <- tstep$sol[,1] #p値をp.valueに格納。 ranking <- rank(abs(p.value)) #p値の順位をrankingに格納。 #ファイルに保存 tmp <- cbind(gene_id, gene_profile, p.value, ranking)#発現変動遺伝子についてのみ、その遺伝子ID、発現データ、p値、その順位を結合した結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存 #以下は(こんなこともできますという)おまけ #発現変動の度合いでソートした結果を得たい場合: out_f2 <- "hoge2.txt" #出力ファイル名を指定してout_fに格納 tmp2 <- tmp[order(ranking),] #順位(rank_masigpro)でソートした結果をtmp2に格納 write.table(tmp2, out_f2, sep="\t", append=F, quote=F, row.names=F)#tmp2の中身を指定したファイル名で保存
2. サンプルデータのsample11_1group.txtとその実験デザインファイル(sample11_1group_cl.txt)の場合:
in_f1 <- "sample11_1group.txt" #入力ファイル名(発現データファイル)を指定してin_f1に格納 in_f2 <- "sample11_1group_cl.txt" #入力ファイル名(実験デザインファイル)を指定してin_f2に格納 out_f <- "hoge2.txt" #出力ファイル名を指定してout_fに格納 param_FDR <- 0.5 #false discovery rate (FDR)閾値を指定 #必要なパッケージをロード library(maSigPro) #パッケージの読み込み #データファイルの読み込み data <- read.table(in_f1, header=TRUE, row.names=1, sep="\t", quote="")#in_f1で指定したファイルの読み込み edesign <- read.table(in_f2, header=TRUE, row.names=1, sep="\t", quote="")#in_f2で指定したファイルの読み込み #本番 design <- make.design.matrix(edesign, degree=2)#実験デザイン行列の作成。degree=2は、2次の回帰モデルで考えることを意味する fit <- p.vector(data, design, Q=param_FDR)#回帰モデルの作成 tstep <- T.fit(fit) #得られた発現変動遺伝子群の各々について最もよい回帰モデルを決める gene_profile <- tstep$sig.profiles #発現変動遺伝子の発現プロファイルをgene_profileに格納。 gene_id <- rownames(gene_profile) #発現変動遺伝子のIDをgene_idに格納。 p.value <- tstep$sol[,1] #p値をp.valueに格納。 ranking <- rank(abs(p.value)) #p値の順位をrankingに格納。 #ファイルに保存 tmp <- cbind(gene_id, gene_profile, p.value, ranking)#発現変動遺伝子についてのみ、その遺伝子ID、発現データ、p値、その順位を結合した結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存 #以下は(こんなこともできますという)おまけ #発現変動の度合いでソートした結果を得たい場合: out_f2 <- "hoge2.txt" #出力ファイル名を指定してout_f2に格納 tmp2 <- tmp[order(ranking),] #順位(rank_masigpro)でソートした結果をtmp2に格納 write.table(tmp2, out_f2, sep="\t", append=F, quote=F, row.names=F)#tmp2の中身を指定したファイル名で保存
解析 | 発現変動 | 時系列 | non-periodic genes | SAM (Tusher_2001)
Significance Analysis of Microarrays (SAM)法で「経時的に発現の変化する遺伝子」のランキングを行う。
注意点:例で用いているsample11_1group.txtの一行目のラベル情報(すなわち、"Time0.5","Time2","Time5","Time12.3","Time24")と同じ形式にしてください。"T_0.5"とか"Time_0.5"などとしてはいけません!
「ファイル」−「ディレクトリの変更」で解析したい対数変換(log2変換)後のファイルを置いてあるディレクトリに移動し、以下をコピペ
1. サンプルデータのsample10_1group.txtの場合:
in_f <- "sample10_1group.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge1.txt" #出力ファイル名を指定してout_fに格納 #必要なパッケージをロード library(samr) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data <- as.matrix(data) #データの型を変換 cl.tmp <- strsplit(colnames(data), "_")#ラベル情報を"One class timecourse"用に変更1 data.cl <- NULL #ラベル情報を"One class timecourse"用に変更2 for(i in 1:ncol(data)){ data.cl[i] <- cl.tmp[[i]][1] }#ラベル情報を"One class timecourse"用に変更3 data.cl <- paste(1, data.cl, sep="") #ラベル情報を"One class timecourse"用に変更4 data.cl[1] <- paste(data.cl[1], "Start", sep="")#ラベル情報を"One class timecourse"用に変更5 data.cl[ncol(data)] <- paste(data.cl[ncol(data)], "End", sep="")#ラベル情報を"One class timecourse"用に変更6 #本番 data.tmp <- list(x=data, y=data.cl, geneid=rownames(data), genenames=rownames(data), logged2=TRUE)#SAMを実行するsamr関数の入力フォーマットに合わせたdata.tmpという入力データを作成 out <- samr(data.tmp, resp.type="One class timecourse", nperms=30, time.summary.type="slope")#samr関数を実行し、結果をsamr.objに格納。 stat_sam <- out$tt #統計量をstat_samに格納。 rank_sam <- rank(-abs(stat_sam)) #統計量の絶対値でランキングした結果をrank_samに格納。 delta.table <- samr.compute.delta.table(out, min.foldchange=0, dels=NULL, nvals=100)#FDRの計算1 out2 <- samr.compute.siggenes.table(out, del, data.tmp, delta.table, min.foldchange=0, all.genes=T)#FDRの計算2 fdr.tmp <- as.numeric(c(out2$genes.up[,7], out2$genes.lo[,7]))#up-regulated側とdown-regulated側の%FDR値をfdr.tmpに格納 fdr.tmp <- fdr.tmp/100 #%FDR値を100で割る names(fdr.tmp) <- c(out2$genes.up[,2], out2$genes.lo[,2])#fdr.tmpはup側とdown側で発現変動の度合いでランキングされているので、遺伝子名との対応づけを行っている fdr_sam <- fdr.tmp[rownames(data)] #もとの入力データの遺伝子名の並びに変更した結果をfdr_samに格納 #ファイルに保存 tmp <- cbind(rownames(data), data, stat_sam, rank_sam, fdr_sam)#読み込んだ元データの右側に統計量、その順位、FDRを追加してtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存 #以下は(こんなこともできますという)おまけ #発現変動の度合いでソートした結果を得たい場合: out_f2 <- "hoge2.txt" #出力ファイル名を指定してout_f2に格納 tmp2 <- tmp[order(rank_sam),] #順位(rank_sam)でソートした結果をtmp2に格納 write.table(tmp2, out_f2, sep="\t", append=F, quote=F, row.names=F)#tmp2の中身を指定したファイル名で保存
2. 発現データファイル: sample11_1group.txt, 実験デザインファイル: sample11_1group_cl.txtの場合:
ここは修正すべし!
in_f1 <- "sample11_1group.txt" #入力ファイル名(発現データファイル)を指定してin_f1に格納 in_f2 <- "sample11_1group_cl.txt" #入力ファイル名(発現デザインファイル)を指定してin_f2に格納 out_f <- "hoge2.txt" #出力ファイル名を指定してout_fに格納 #必要なパッケージをロード library(samr) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f1, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data <- as.matrix(data) #データの型を変換 data.cl <- paste(1, colnames(data), sep="")#ラベル情報を"One class timecourse"用に変更1 data.cl[1] <- paste(data.cl[1], "Start", sep="")#ラベル情報を"One class timecourse"用に変更2 data.cl[ncol(data)] <- paste(data.cl[ncol(data)], "End", sep="")#ラベル情報を"One class timecourse"用に変更3 #本番 data.tmp <- list(x=data, y=data.cl, geneid=rownames(data), genenames=rownames(data), logged2=TRUE)#SAMを実行するsamr関数の入力フォーマットに合わせたdata.tmpという入力データを作成 out <- samr(data.tmp, resp.type="One class timecourse", nperms=30, time.summary.type="slope")#samr関数を実行し、結果をsamr.objに格納。 stat_sam <- out$tt #統計量をstat_samに格納。 rank_sam <- rank(-abs(stat_sam)) #統計量の絶対値でランキングした結果をrank_samに格納。 delta.table <- samr.compute.delta.table(out, min.foldchange=0, dels=NULL, nvals=100)#FDRの計算1 out2 <- samr.compute.siggenes.table(out, del, data.tmp, delta.table, min.foldchange=0, all.genes=T)#FDRの計算2 fdr.tmp <- as.numeric(c(out2$genes.up[,7], out2$genes.lo[,7]))#up-regulated側とdown-regulated側の%FDR値をfdr.tmpに格納 fdr.tmp <- fdr.tmp/100 #%FDR値を100で割る names(fdr.tmp) <- c(out2$genes.up[,2], out2$genes.lo[,2])#fdr.tmpはup側とdown側で発現変動の度合いでランキングされているので、遺伝子名との対応づけを行っている fdr_sam <- fdr.tmp[rownames(data)] #もとの入力データの遺伝子名の並びに変更した結果をfdr_samに格納 #ファイルに保存 tmp <- cbind(rownames(data), data, stat_sam, rank_sam, fdr_sam)#読み込んだ元データの右側に統計量、その順位、FDRを追加してtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存 #以下は(こんなこともできますという)おまけ #発現変動の度合いでソートした結果を得たい場合: out_f2 <- "hoge2.txt" #出力ファイル名を指定してout_f2に格納 tmp2 <- tmp[order(rank_sam),] #順位(rank_sam)でソートした結果をtmp2に格納 write.table(tmp2, out_f2, sep="\t", append=F, quote=F, row.names=F)#tmp2の中身を指定したファイル名で保存
sample11の解析結果のhoge2.txtにおいて、rank_samのランキング結果とFDR値(fdr_sam)の対応がちゃんととれていないのは、up-regulated側とdown-regulated側がごちゃまぜになっているためです。
例えば、stat_sam列でソートすると、FDR値の分布がきれい?!になります。fdr_sam列でソートすると、例えばFDR <=0.33...を満たすのは上位3個(gene713, 781, and 492)ですが、このうちの33.3...%(i.e., 3分の1個)は"偽物"という風に解釈します。
解析 | 機能解析 | 遺伝子オントロジー(GO)解析 | について
機能解析の実体は遺伝子セット解析です。遺伝子セット解析としてGO termを利用するのがGO解析です。
R用:
- globaltest:Goeman et al., Bioinformatics, 2004
- SAFE:Barry et al., Bioinformatics, 2005
- topGO:Alexa et al., Bioinformatics, 2006
- pcot2:Kong et al., Bioinformatics, 2006
- Category:Jiang et al., Bioinformatics, 2007
- GSA (作者のGSAウェブページ):Efron and Tibshirani, Ann. Appl. Stat., 2007
- dCoxS:Cho et al., BMC Bioinformatics, 2009
- GAGE:Luo et al., BMC Bioinformatics, 2009
- GOSemSim:Yu et al., Bioinformatics, 2010
- Camera (limmaの一部, 分かりづらい):We et al., Nucleic Acids Res., 2012
- RamiGO:Schröder et al., Bioinformatics, 2013
- LCT:Dinu et al., BMC Bioinformatics, 2013
- GSNCA法(GSARで提供されている):Rahmatallah et al., Bioinformatics, 2014
- TcGSA(時系列データ解析用):Hejblum et al., PLoS Comput Biol., 2015
- CompGO:Waardenberg et al., BMC Bioinformatics, 2015
- EnrichmentBrowser:Geistlinger et al., BMC Bioinformatics, 2016
- GOexpress:Rue-Albrecht et al., BMC Bioinformatics, 2016
- GSAR:Rahmatallah et al., BMC Bioinformatics, 2017
R以外:
- GSEA:Subramanian et al., PNAS, 2005
- GSEAのユーザーガイド
- 名前とプログラムなし:Jiang and Gentleman, Bioinformatics, 2007
- GeneTrail:Backes et al., NAR, 2007
- SAM-GS (Excel Add-Inらしい):Dinu et al., BMC Bioinformatics, 2007
- GSEA-P:Subramanian et al., Bioinformatics, 2007
- MR-GSE (プログラム自体は公開していない模様):Michaud et al., BMC Genomics, 2008
- GeneTrailExpress:Keller et al., BMC Bioinformatics, 2008
- QuickGO:Binns et al., Bioinformatics, 2009
- EnrichNet:Glaab et al., Bioinformatics, 2012
- JEPETTO:Winterhalter et al., Bioinformatics, 2014
- EDDY:Jung et al., Nucleic Acids Res., 2014
- MMGSA (プログラム公開の有無は不明):Khodakarim et al., Gene, 2014
Review、ガイドライン、パイプライン系:
遺伝子セットDB系:
GSEAに代表される発現変動遺伝子セット解析は、基本的にGSEAの開発者らが作成した様々な遺伝子セット情報を収めた Molecular Signatures Database (MSigDB)からダウンロードした.gmt形式ファイルを読み込んで解析を行います。 それゆえ、自分がどの遺伝子セットについて機能解析を行いたいのかを予め決めておく必要がありますが、GO解析の場合はbiological process (BP)が一般的なようです。 2015/06/07時点は ver. 5.0、2017/03/08時点はver. 5.2です。 gmt形式ファイルの基本的なダウンロード方法は以下の通りです:
- Molecular Signatures Database (MSigDB)の
「register」のページで登録し、遺伝子セットをダウンロード可能な状態にする。 - Molecular Signatures Database (MSigDB)の
「Download gene sets」の"Download"のところをクリックし、Loginページで登録したe-mail addressを入力。 - これでMSigDBのダウンロードページに行けるので、目的に応じたgmtファイルをダウンロードしておく。
「c5: gene ontology gene sets」の「bp: biological process」を解析する場合:c5.bp.v5.0.symbols.gmt
「c5: gene ontology gene sets」の「cc: cellular components」を解析する場合:c5.cc.v5.0.symbols.gmt
「c5: gene ontology gene sets」の「mf: molecular functions」を解析する場合:c5.mf.v5.0.symbols.gmt
解析 | 機能解析 | 遺伝子オントロジー(GO)解析 | GSAR (Rahmatallah_2017)
GSARパッケージを用いた解析のやり方を示します。 GSARは、様々なプログラム群からなるパッケージです。 ここでは、GSARで提供されているGene Sets Net Correlations Analysis法(GSNCA; Rahmatallah et al., 2014)を実行するやり方を示します。 オリジナルのprobeset IDからgene symbolにID変換がなされた発現データファイルを入力としています。 これは、「イントロ | アノテーション情報取得 | GEOquery(Davis_2007)」 で入手したprobeset IDとgene symbolの対応表のファイル、およびオリジナルのprobeset IDごとの発現データファイルを用いて 「前処理 | ID変換 | probe ID --> gene symbol」 でID変換したものです。gmtファイルは、MSigDB (Subramanian et al., PNAS, 2005)から任意のものをダウンロードしてください。 尚、gmtファイルの読み込みにはGSAパッケージ (Efron and Tibshirani, 2007)中のGSA.read.gmt関数を利用しています。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し以下をコピペ。
1.data_mas_EN_symbol.txtの場合:
14,132 genes×24 samplesのデータです。BAT_fed vs. BAT_fastedの2群間比較を行うべく、それらの位置情報を指定しています。 「解析 | 機能解析 | パスウェイ(Pathway)解析 | GSAR (Rahmatallah_2017)」の例題7と 「解析 | 機能解析 | 遺伝子オントロジー(GO)解析 | GSA (Efron_2007)」の例題3を合わせたものです。 ここでは、"STEROID_BIOSYNTHETIC_PROCESS"という遺伝子セットのネットワーク図をpngファイルに出力させています。
in_f1 <- "data_mas_EN_symbol.txt" #入力ファイル名を指定してin_f1に格納(発現データファイル) in_f2 <- "c5.bp.v5.0.symbols.gmt" #入力ファイル名を指定してin_f2に格納(gmtファイル) out_f <- "hoge1.png" #出力ファイル名を指定してout_fに格納 param_G1 <- 4 #G1群のサンプル数を指定 param_G2 <- 4 #G2群のサンプル数を指定 param_FDR <- 0.1 #false discovery rate (FDR)閾値を指定 param_posi <- c(1:4, 5:8) #G1群およびG2群の位置情報を指定 param <- "STEROID_BIOSYNTHETIC_PROCESS"#解析したい遺伝子セット名を指定 param_fig <- c(700, 650) #ファイル出力時の横幅と縦幅を指定(単位はピクセル) #必要なパッケージをロード library(GSAR) #パッケージの読み込み library(GSA) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成、そしてサブセットの作成 data <- read.table(in_f1, header=TRUE, row.names=1, sep="\t", quote="")#in_f1で指定したファイルの読み込み rownames(data) <- toupper(rownames(data))#IDを大文字に変換している(gmtファイルに合わせるため) data <- as.matrix(data) #型変換(TestGeneSets関数が要求しているため) data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 data <- data[,param_posi] #サブセットを抽出 colnames(data) #確認してるだけです hoge <- GSA.read.gmt(in_f2) #in_f2で指定したファイルの読み込み(不完全な最終行が見つかりました、となっても気にしない) gmt <- hoge$genesets #フォーマット変換 names(gmt) <- hoge$geneset.names #フォーマット変換 #GSAR本番(正確にはGSARから提供されているGSNCA法の実行) set.seed(1053) #おまじない(同じ乱数になるようにするため) hoge <- gmt[[param]] #解析したい遺伝子セット情報をhogeに格納 length(hoge) #遺伝子数を表示(gmtファイル) obj <- is.element(rownames(data), hoge)#条件判定 sum(obj) #遺伝子数を表示(発現データ中に存在するものに限定) p.value <- GSNCAtest(data[obj, ], data.cl)#GSNCAを実行 p.value #p-valueを表示 #ファイルに保存(相関ネットワーク(correlation network)図) png(out_f, pointsize=13, width=param_fig[1], height=param_fig[2])#出力ファイルの各種パラメータを指定 plotMST2.pathway(object=data[obj, ], #相関ネットワーク(correlation network)図の作成 group=data.cl, name=param, #相関ネットワーク(correlation network)図の作成 legend.size=1.2, leg.x=-1.2, #相関ネットワーク(correlation network)図の作成 leg.y=2, label.size=1, #相関ネットワーク(correlation network)図の作成 label.dist=0.8, cor.method="pearson")#相関ネットワーク(correlation network)図の作成 dev.off() #おまじない
2.サンプルデータ20のdata_rma_2_nr.txtの場合:
14,132 genes×24 samplesのデータです。BAT_fed vs. BAT_fastedの2群間比較を行うべく、それらの位置情報を指定しています。 「解析 | 機能解析 | パスウェイ(Pathway)解析 | GSAR (Rahmatallah_2017)」の例題7と 「解析 | 機能解析 | 遺伝子オントロジー(GO)解析 | GSA (Efron_2007)」の例題3を合わせたものです。 ここでは、"STEROID_BIOSYNTHETIC_PROCESS"という遺伝子セットのネットワーク図をpngファイルに出力させています。
in_f1 <- "data_rma_2_nr.txt" #入力ファイル名を指定してin_f1に格納(発現データファイル) in_f2 <- "c5.bp.v5.0.symbols.gmt" #入力ファイル名を指定してin_f2に格納(gmtファイル) out_f <- "hoge2.png" #出力ファイル名を指定してout_fに格納 param_G1 <- 4 #G1群のサンプル数を指定 param_G2 <- 4 #G2群のサンプル数を指定 param_FDR <- 0.1 #false discovery rate (FDR)閾値を指定 param_posi <- c(1:4, 5:8) #G1群およびG2群の位置情報を指定 param <- "STEROID_BIOSYNTHETIC_PROCESS"#解析したい遺伝子セット名を指定 param_fig <- c(700, 650) #ファイル出力時の横幅と縦幅を指定(単位はピクセル) #必要なパッケージをロード library(GSAR) #パッケージの読み込み library(GSA) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成、そしてサブセットの作成 data <- read.table(in_f1, header=TRUE, row.names=1, sep="\t", quote="")#in_f1で指定したファイルの読み込み rownames(data) <- toupper(rownames(data))#IDを大文字に変換している(gmtファイルに合わせるため) data <- as.matrix(data) #型変換(TestGeneSets関数が要求しているため) data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 data <- data[,param_posi] #サブセットを抽出 colnames(data) #確認してるだけです hoge <- GSA.read.gmt(in_f2) #in_f2で指定したファイルの読み込み(不完全な最終行が見つかりました、となっても気にしない) gmt <- hoge$genesets #フォーマット変換 names(gmt) <- hoge$geneset.names #フォーマット変換 #GSAR本番(正確にはGSARから提供されているGSNCA法の実行) set.seed(1053) #おまじない(同じ乱数になるようにするため) hoge <- gmt[[param]] #解析したい遺伝子セット情報をhogeに格納 length(hoge) #遺伝子数を表示(gmtファイル) obj <- is.element(rownames(data), hoge)#条件判定 sum(obj) #遺伝子数を表示(発現データ中に存在するものに限定) p.value <- GSNCAtest(data[obj, ], data.cl)#GSNCAを実行 p.value #p-valueを表示 #ファイルに保存(相関ネットワーク(correlation network)図) png(out_f, pointsize=13, width=param_fig[1], height=param_fig[2])#出力ファイルの各種パラメータを指定 plotMST2.pathway(object=data[obj, ], #相関ネットワーク(correlation network)図の作成 group=data.cl, name=param, #相関ネットワーク(correlation network)図の作成 legend.size=1.2, leg.x=-1.2, #相関ネットワーク(correlation network)図の作成 leg.y=2, label.size=1, #相関ネットワーク(correlation network)図の作成 label.dist=0.8, cor.method="pearson")#相関ネットワーク(correlation network)図の作成 dev.off() #おまじない
解析 | 機能解析 | 遺伝子オントロジー(GO)解析 | GAGE (Luo_2009)
gageパッケージを用いた解析のやり方を示します。 原著論文では方法名はGAGEですが、Rパッケージ名はgageです。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し以下をコピペ。
1. ...の場合:
library(gage) #パッケージの読み込み
解析 | 機能解析 | 遺伝子オントロジー(GO)解析 | GSA (Efron_2007)
GSAパッケージを用いた解析のやり方を示します。 オリジナルのprobeset IDからgene symbolにID変換がなされた発現データファイルを入力としています。 これは、「イントロ | アノテーション情報取得 | GEOquery(Davis_2007)」 で入手したprobeset IDとgene symbolの対応表のファイル、およびオリジナルのprobeset IDごとの発現データファイルを用いて 「前処理 | ID変換 | probe ID --> gene symbol」 でID変換したものです。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し以下をコピペ。
1.サンプルデータ20のdata_rma_2_nr_LIV.txtの場合:
肝臓のみからなる14,132 genes×8 samplesのデータです。LIV_fed vs. LIV_fastedの2群間比較です。
in_f1 <- "data_rma_2_nr_LIV.txt" #入力ファイル名を指定してin_f1に格納(発現データファイル) in_f2 <- "c5.bp.v5.0.symbols.gmt" #入力ファイル名を指定してin_f2に格納(gmtファイル) out_f1 <- "hoge1_G1.txt" #出力ファイル名を指定してout_f1に格納(G1群で高発現の遺伝子セットリスト) out_f2 <- "hoge1_G2.txt" #出力ファイル名を指定してout_f2に格納(G2群で高発現の遺伝子セットリスト) param_G1 <- 4 #G1群のサンプル数を指定 param_G2 <- 4 #G2群のサンプル数を指定 param_FDR <- 0.1 #false discovery rate (FDR)閾値を指定 #必要なパッケージをロード library(GSA) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成 gmt <- GSA.read.gmt(in_f2) #in_f2で指定したファイルの読み込み(不完全な最終行が見つかりました、となっても気にしない) data <- read.table(in_f1, header=TRUE, row.names=1, sep="\t", quote="")#in_f1で指定したファイルの読み込み rownames(data) <- toupper(rownames(data))#gene symbolを大文字に変換している(gmtファイルに合わせるため) data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #GSA本番 out <- GSA(data, data.cl, #GSAを実行し、結果をoutに格納 genesets=gmt$genesets, #GSAを実行し、結果をoutに格納 genenames=rownames(data), #GSAを実行し、結果をoutに格納 resp.type="Two class unpaired")#GSAを実行し、結果をoutに格納 tmp <- GSA.listsets(out, #param_FDRで指定したFDR閾値を満たす遺伝子セットのみリストアップした結果をtmpに格納 geneset.names=gmt$geneset.names,#param_FDRで指定したFDR閾値を満たす遺伝子セットのみリストアップした結果をtmpに格納 maxchar=max(nchar(gmt$geneset.names)),#param_FDRで指定したFDR閾値を満たす遺伝子セットのみリストアップした結果をtmpに格納 FDRcut=param_FDR) #param_FDRで指定したFDR閾値を満たす遺伝子セットのみリストアップした結果をtmpに格納 #ファイルに保存 write.table(tmp$negative, out_f1, sep="\t", append=F, quote=F, row.names=F)#tmp$negativeの中身を指定したファイル名で保存 write.table(tmp$positive, out_f2, sep="\t", append=F, quote=F, row.names=F)#tmp$positiveの中身を指定したファイル名で保存
2.サンプルデータ20のdata_rma_2_nr.txtの場合:
14,132 genes×24 samplesのデータです。 LIV_fed vs. LIV_fastedの2群間比較を行うべく、それらの位置情報を指定しています。
in_f1 <- "data_rma_2_nr.txt" #入力ファイル名を指定してin_f1に格納(発現データファイル) in_f2 <- "c5.bp.v5.0.symbols.gmt" #入力ファイル名を指定してin_f2に格納(gmtファイル) out_f1 <- "hoge2_G1.txt" #出力ファイル名を指定してout_f1に格納(G1群で高発現の遺伝子セットリスト) out_f2 <- "hoge2_G2.txt" #出力ファイル名を指定してout_f2に格納(G2群で高発現の遺伝子セットリスト) param_G1 <- 4 #G1群のサンプル数を指定 param_G2 <- 4 #G2群のサンプル数を指定 param_FDR <- 0.1 #false discovery rate (FDR)閾値を指定 param_posi <- c(17:20, 21:24) #G1群およびG2群の位置情報を指定 #必要なパッケージをロード library(GSA) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成、そしてサブセットの作成 gmt <- GSA.read.gmt(in_f2) #in_f2で指定したファイルの読み込み(不完全な最終行が見つかりました、となっても気にしない) data <- read.table(in_f1, header=TRUE, row.names=1, sep="\t", quote="")#in_f1で指定したファイルの読み込み rownames(data) <- toupper(rownames(data))#IDを大文字に変換している(gmtファイルに合わせるため) data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 data <- data[,param_posi] #サブセットを抽出 colnames(data) #確認してるだけです #GSA本番 out <- GSA(data, data.cl, #GSAを実行し、結果をoutに格納 genesets=gmt$genesets, #GSAを実行し、結果をoutに格納 genenames=rownames(data), #GSAを実行し、結果をoutに格納 resp.type="Two class unpaired")#GSAを実行し、結果をoutに格納 tmp <- GSA.listsets(out, #param_FDRで指定したFDR閾値を満たす遺伝子セットのみリストアップした結果をtmpに格納 geneset.names=gmt$geneset.names,#param_FDRで指定したFDR閾値を満たす遺伝子セットのみリストアップした結果をtmpに格納 maxchar=max(nchar(gmt$geneset.names)),#param_FDRで指定したFDR閾値を満たす遺伝子セットのみリストアップした結果をtmpに格納 FDRcut=param_FDR) #param_FDRで指定したFDR閾値を満たす遺伝子セットのみリストアップした結果をtmpに格納 #ファイルに保存 write.table(tmp$negative, out_f1, sep="\t", append=F, quote=F, row.names=F)#tmp$negativeの中身を指定したファイル名で保存 write.table(tmp$positive, out_f2, sep="\t", append=F, quote=F, row.names=F)#tmp$positiveの中身を指定したファイル名で保存
3.サンプルデータ20のdata_rma_2_nr.txtの場合:
14,132 genes×24 samplesのデータです。BAT_fed vs. BAT_fastedの2群間比較を行うべく、それらの位置情報を指定しています。
in_f1 <- "data_rma_2_nr.txt" #入力ファイル名を指定してin_f1に格納(発現データファイル) in_f2 <- "c5.bp.v5.0.symbols.gmt" #入力ファイル名を指定してin_f2に格納(gmtファイル) out_f1 <- "hoge3_G1.txt" #出力ファイル名を指定してout_f1に格納(G1群で高発現の遺伝子セットリスト) out_f2 <- "hoge3_G2.txt" #出力ファイル名を指定してout_f2に格納(G2群で高発現の遺伝子セットリスト) param_G1 <- 4 #G1群のサンプル数を指定 param_G2 <- 4 #G2群のサンプル数を指定 param_FDR <- 0.1 #false discovery rate (FDR)閾値を指定 param_posi <- c(1:4, 5:8) #G1群およびG2群の位置情報を指定 #必要なパッケージをロード library(GSA) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成、そしてサブセットの作成 gmt <- GSA.read.gmt(in_f2) #in_f2で指定したファイルの読み込み(不完全な最終行が見つかりました、となっても気にしない) data <- read.table(in_f1, header=TRUE, row.names=1, sep="\t", quote="")#in_f1で指定したファイルの読み込み rownames(data) <- toupper(rownames(data))#IDを大文字に変換している(gmtファイルに合わせるため) data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 data <- data[,param_posi] #サブセットを抽出 colnames(data) #確認してるだけです #GSA本番 out <- GSA(data, data.cl, #GSAを実行し、結果をoutに格納 genesets=gmt$genesets, #GSAを実行し、結果をoutに格納 genenames=rownames(data), #GSAを実行し、結果をoutに格納 resp.type="Two class unpaired")#GSAを実行し、結果をoutに格納 tmp <- GSA.listsets(out, #param_FDRで指定したFDR閾値を満たす遺伝子セットのみリストアップした結果をtmpに格納 geneset.names=gmt$geneset.names,#param_FDRで指定したFDR閾値を満たす遺伝子セットのみリストアップした結果をtmpに格納 maxchar=max(nchar(gmt$geneset.names)),#param_FDRで指定したFDR閾値を満たす遺伝子セットのみリストアップした結果をtmpに格納 FDRcut=param_FDR) #param_FDRで指定したFDR閾値を満たす遺伝子セットのみリストアップした結果をtmpに格納 #ファイルに保存 write.table(tmp$negative, out_f1, sep="\t", append=F, quote=F, row.names=F)#tmp$negativeの中身を指定したファイル名で保存 write.table(tmp$positive, out_f2, sep="\t", append=F, quote=F, row.names=F)#tmp$positiveの中身を指定したファイル名で保存
4.サンプルデータ20のdata_rma_2_nr.txtの場合:
3.と基本的に同じですが、並べ替え検定時の並べ替え回数(nperms;デフォルトは200)を自在に変更するやり方です。
in_f1 <- "data_rma_2_nr.txt" #入力ファイル名を指定してin_f1に格納(発現データファイル) in_f2 <- "c5.bp.v5.0.symbols.gmt" #入力ファイル名を指定してin_f2に格納(gmtファイル) out_f1 <- "hoge4_G1.txt" #出力ファイル名を指定してout_f1に格納(G1群で高発現の遺伝子セットリスト) out_f2 <- "hoge4_G2.txt" #出力ファイル名を指定してout_f2に格納(G2群で高発現の遺伝子セットリスト) param_G1 <- 4 #G1群のサンプル数を指定 param_G2 <- 4 #G2群のサンプル数を指定 param_FDR <- 0.1 #false discovery rate (FDR)閾値を指定 param_posi <- c(1:4, 5:8) #G1群およびG2群の位置情報を指定 param_perm <- 100 #並べ替え回数を指定(数値が大きいほどより正確だがその分だけ時間がかかる。実際の解析ではサンプル数にもよるが最低でも1000以上を推奨) #必要なパッケージをロード library(GSA) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成、そしてサブセットの作成 gmt <- GSA.read.gmt(in_f2) #in_f2で指定したファイルの読み込み(不完全な最終行が見つかりました、となっても気にしない) data <- read.table(in_f1, header=TRUE, row.names=1, sep="\t", quote="")#in_f1で指定したファイルの読み込み rownames(data) <- toupper(rownames(data))#IDを大文字に変換している(gmtファイルに合わせるため) data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 data <- data[,param_posi] #サブセットを抽出 colnames(data) #確認してるだけです #GSA本番 out <- GSA(data, data.cl, #GSAを実行し、結果をoutに格納 genesets=gmt$genesets, #GSAを実行し、結果をoutに格納 genenames=rownames(data), #GSAを実行し、結果をoutに格納 resp.type="Two class unpaired",#GSAを実行し、結果をoutに格納 nperms=param_perm) #GSAを実行し、結果をoutに格納 tmp <- GSA.listsets(out, #param_FDRで指定したFDR閾値を満たす遺伝子セットのみリストアップした結果をtmpに格納 geneset.names=gmt$geneset.names,#param_FDRで指定したFDR閾値を満たす遺伝子セットのみリストアップした結果をtmpに格納 maxchar=max(nchar(gmt$geneset.names)),#param_FDRで指定したFDR閾値を満たす遺伝子セットのみリストアップした結果をtmpに格納 FDRcut=param_FDR) #param_FDRで指定したFDR閾値を満たす遺伝子セットのみリストアップした結果をtmpに格納 #ファイルに保存 write.table(tmp$negative, out_f1, sep="\t", append=F, quote=F, row.names=F)#tmp$negativeの中身を指定したファイル名で保存 write.table(tmp$positive, out_f2, sep="\t", append=F, quote=F, row.names=F)#tmp$positiveの中身を指定したファイル名で保存
解析 | 機能解析 | 遺伝子オントロジー(GO)解析 | Category (Jiang_2007)
Categoryパッケージを用いた解析のやり方を示します。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し以下をコピペ。
1. ...の場合:
library(Category) #パッケージの読み込み
解析 | 機能解析 | 遺伝子オントロジー(GO)解析 | pcot2 (Kong_2006)
pcot2パッケージを用いた解析のやり方を示します。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し以下をコピペ。
1. ...の場合:
library(pcot2) #パッケージの読み込み
解析 | 機能解析 | 遺伝子オントロジー(GO)解析 | topGO (Alexa_2006)
globaltestパッケージを用いた解析のやり方を示します。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し以下をコピペ。
1. ...の場合:
library(topGO) #パッケージの読み込み
解析 | 機能解析 | 遺伝子オントロジー(GO)解析 | SAFE (Barry_2005)
SAFEパッケージを用いた解析のやり方を示します。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し以下をコピペ。
1. ...の場合:
library(SAFE) #パッケージの読み込み
解析 | 機能解析 | 遺伝子オントロジー(GO)解析 | globaltest (Goeman_2004)
globaltestパッケージを用いた解析のやり方を示します。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し以下をコピペ。
1. ...の場合:
library(globaltest) #パッケージの読み込み
解析 | 機能解析 | パスウェイ(Pathway)解析 | について
機能解析の実体は遺伝子セット解析です。遺伝子セット解析としてKEGGなどのパスウェイ情報を利用するのがパスウェイ解析です。
R用:
- GSA (作者のGSAウェブページ):Efron and Tibshirani, Ann. Appl. Stat., 2007
- SPIA:Tarca et al., Bioinformatics, 2009
- dCoxS:Cho et al., BMC Bioinformatics, 2009
- GAGE:Luo et al., BMC Bioinformatics, 2009
- PADOG:Tarca et al., BMC Bioinformatics, 2012
- Pathview:Luo et al., Bioinformatics, 2013
- GSNCA法(GSARで提供されている):Rahmatallah et al., Bioinformatics, 2014
- TcGSA(時系列データ解析用):Hejblum et al., PLoS Comput Biol., 2015
- EnrichmentBrowser:Geistlinger et al., BMC Bioinformatics, 2016
- GSAR:Rahmatallah et al., BMC Bioinformatics, 2017
R以外:
- PLAGE(リンク切れ):Tomfohr et al., BMC Bioinformatics, 2005
- GSEA:Subramanian et al., PNAS, 2005
- GSEAのユーザーガイド
- ToppGene Suite(loginも要求なし; webtool):Chen et al., Nucleic Acids Res., 2009
- PINTA(loginも要求なし; webtool):Nitsch et al., Nucleic Acids Res., 2011
- FIDEA(loginも要求なし; webtool):D'Andrea et al., Nucleic Acids Res., 2013
Review、ガイドライン、パイプライン系:
遺伝子セットDB系:
GSEAに代表される発現変動遺伝子セット解析は、基本的にGSEAの開発者らが作成した様々な遺伝子セット情報を収めた Molecular Signatures Database (MSigDB)からダウンロードした.gmt形式ファイルを読み込んで解析を行います。 それゆえ、自分がどの遺伝子セットについて機能解析を行いたいのかを予め決めておく必要がありますが、 パスウェイ解析の場合はc2のBioCarta, KEGG, Reactomeあたりを解析するのでしょう。 2015/06/07時点は ver. 5.0、2017/03/08時点はver. 5.2です。 gmt形式ファイルの基本的なダウンロード方法は以下の通りです:
- Molecular Signatures Database (MSigDB)の
「register」のページで登録し、遺伝子セットをダウンロード可能な状態にする。 - Molecular Signatures Database (MSigDB)の
「Download gene sets」の"Download"のところをクリックし、Loginページで登録したe-mail addressを入力。 - これでMSigDBのダウンロードページに行けるので、目的に応じたgmtファイルをダウンロード。
「c2: curated gene sets」の「all canonical pathways, gene symbols」を解析する場合:c2.cp.v5.0.symbols.gmt
「c2: curated gene sets」の「BioCarta gene sets, gene symbols」を解析する場合:c2.cp.biocarta.v5.0.symbols.gmt
「c2: curated gene sets」の「KEGG gene sets, gene symbols」を解析する場合:c2.cp.kegg.v5.0.symbols.gmt
「c2: curated gene sets」の「Reactome gene sets, gene symbols」を解析する場合:c2.cp.reactome.v5.0.symbols.gmt
解析 | 機能解析 | パスウェイ(Pathway)解析 | GSAR (Rahmatallah_2017)
GSARパッケージを用いた解析のやり方を示します。 GSARは、様々なプログラム群からなるパッケージです。 ここでは、GSARで提供されているGene Sets Net Correlations Analysis法(GSNCA; Rahmatallah et al., 2014)を実行するやり方を示します。 オリジナルのprobeset IDからgene symbolにID変換がなされた発現データファイルを入力としています。 これは、「イントロ | アノテーション情報取得 | GEOquery(Davis_2007)」 で入手したprobeset IDとgene symbolの対応表のファイル、およびオリジナルのprobeset IDごとの発現データファイルを用いて 「前処理 | ID変換 | probe ID --> gene symbol」 でID変換したものです。gmtファイルは、MSigDB (Subramanian et al., PNAS, 2005)から任意のものをダウンロードしてください。 尚、gmtファイルの読み込みにはGSAパッケージ (Efron and Tibshirani, 2007)中のGSA.read.gmt関数を利用しています。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し以下をコピペ。
1. GSARの解析例として示されているp53 datasetの場合:
p53DataSetという名前の8,655 genes×50 samplesのデータです。 17 wild-type (WT) samples vs. 33 mutant (MUT) samplesの2群間比較です。 gmtファイルは、MSigDB (ver. 5.2)の C2: curated gene sets中の 全データファイル(c2.all.v5.2.symbols.gmt)を利用しています。 この中に解析例で取り扱っている遺伝子セット("LU_TUMOR_VASCULATURE_UP")が含まれています。 ここでは、"LU_TUMOR_VASCULATURE_UP"を構成する遺伝子群(29 genes)の中から、 発現データ中に存在するもの(22 genes)に対してGSNCA法を適用した結果のp-value (= 0.02797)を出力するところまでを示します。 p-value = 0.02797という結果は、比較する2群間(WT vs. MUT)でこの遺伝子セットの発現の相関に差がない(帰無仮説)確率が2.797%しかないことを意味します。 1つの判断基準として、(建前上)有意水準α = 0.05を設定していたのなら、帰無仮説が本当は正しいが間違って棄却してしまう確率を5%に設定したことに相当し、 この場合はp-value < 0.05なので帰無仮説を棄却し対立仮説(差がある)を採択することになります。
in_f <- "c2.all.v5.2.symbols.gmt" #入力ファイル名を指定してin_fに格納(gmtファイル) param_G1 <- 17 #G1群のサンプル数を指定 param_G2 <- 33 #G2群のサンプル数を指定 param <- "LU_TUMOR_VASCULATURE_UP" #解析したい遺伝子セット名を指定 #必要なパッケージをロード library(GSAR) #パッケージの読み込み library(GSA) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成 hoge <- GSA.read.gmt(in_f) #in_fで指定したファイルの読み込み(不完全な最終行が見つかりました、となっても気にしない) gmt <- hoge$genesets #フォーマット変換 names(gmt) <- hoge$geneset.names #フォーマット変換 data(p53DataSet) #GSARパッケージ中のp53DataSetオブジェクトの呼び出し data <- p53DataSet #オブジェクト名の変更(dataとして取り扱う) rownames(data) <- toupper(rownames(data))#gene symbolを大文字に変換している(gmtファイルに合わせるため) dim(data) #確認してるだけです data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #GSAR本番(正確にはGSARから提供されているGSNCA法の実行) set.seed(1053) #おまじない(同じ乱数になるようにするため) hoge <- gmt[[param]] #解析したい遺伝子セット情報をhogeに格納 length(hoge) #遺伝子数を表示(gmtファイル) obj <- is.element(rownames(data), hoge)#条件判定 sum(obj) #遺伝子数を表示(発現データ中に存在するものに限定) p.value <- GSNCAtest(data[obj, ], data.cl)#GSNCAを実行 p.value #p-valueを表示
2. GSARの解析例として示されているp53 datasetの場合:
1.と基本的に同じですが、さらに相関ネットワーク(correlation network)図も描いています。 グループごとに独立にネットワークが描画され、Group1(WT)の相関ネットワークが左側に、 そしてGroup2(MUT)の相関ネットワークが右側に描画されます。 p-value = 0.02797の遺伝子セットの相関ネットワークなので、差がある(i.e., あまりにも似ていない)ことがわかっています。 図の上のほうに、グループごとの最有力遺伝子(most influential genes or hub genes)が示されています。 この場合は、Group1(WT)がTNFAIP6、そしてGroup2(MUT)がVCANとなっていることがわかります。 この図自体はp-valueの大小に関わらず描くことができます。
in_f <- "c2.all.v5.2.symbols.gmt" #入力ファイル名を指定してin_fに格納(gmtファイル) param_G1 <- 17 #G1群のサンプル数を指定 param_G2 <- 33 #G2群のサンプル数を指定 param <- "LU_TUMOR_VASCULATURE_UP" #解析したい遺伝子セット名を指定 #必要なパッケージをロード library(GSAR) #パッケージの読み込み library(GSA) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成 hoge <- GSA.read.gmt(in_f) #in_fで指定したファイルの読み込み(不完全な最終行が見つかりました、となっても気にしない) gmt <- hoge$genesets #フォーマット変換 names(gmt) <- hoge$geneset.names #フォーマット変換 data(p53DataSet) #GSARパッケージ中のp53DataSetオブジェクトの呼び出し data <- p53DataSet #オブジェクト名の変更(dataとして取り扱う) rownames(data) <- toupper(rownames(data))#gene symbolを大文字に変換している(gmtファイルに合わせるため) dim(data) #確認してるだけです data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #GSAR本番(正確にはGSARから提供されているGSNCA法の実行) set.seed(1053) #おまじない(同じ乱数になるようにするため) hoge <- gmt[[param]] #解析したい遺伝子セット情報をhogeに格納 length(hoge) #遺伝子数を表示(gmtファイル) obj <- is.element(rownames(data), hoge)#条件判定 sum(obj) #遺伝子数を表示(発現データ中に存在するものに限定) p.value <- GSNCAtest(data[obj, ], data.cl)#GSNCAを実行 p.value #p-valueを表示 #作図(相関ネットワーク(correlation network)) plotMST2.pathway(object=data[obj, ], #相関ネットワーク(correlation network)図の作成 group=data.cl, name=param, #相関ネットワーク(correlation network)図の作成 legend.size=1.2, leg.x=-1.2, #相関ネットワーク(correlation network)図の作成 leg.y=2, label.size=1, #相関ネットワーク(correlation network)図の作成 label.dist=0.8, cor.method="pearson")#相関ネットワーク(correlation network)図の作成
3. GSARの解析例として示されているp53 datasetの場合:
2.と基本的に同じですが、相関ネットワーク(correlation network)図をpngファイルに保存しています。
in_f <- "c2.all.v5.2.symbols.gmt" #入力ファイル名を指定してin_fに格納(gmtファイル) out_f <- "hoge3.png" #出力ファイル名を指定してout_fに格納 param_G1 <- 17 #G1群のサンプル数を指定 param_G2 <- 33 #G2群のサンプル数を指定 param <- "LU_TUMOR_VASCULATURE_UP" #解析したい遺伝子セット名を指定 param_fig <- c(700, 650) #ファイル出力時の横幅と縦幅を指定(単位はピクセル) #必要なパッケージをロード library(GSAR) #パッケージの読み込み library(GSA) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成 hoge <- GSA.read.gmt(in_f) #in_fで指定したファイルの読み込み(不完全な最終行が見つかりました、となっても気にしない) gmt <- hoge$genesets #フォーマット変換 names(gmt) <- hoge$geneset.names #フォーマット変換 data(p53DataSet) #GSARパッケージ中のp53DataSetオブジェクトの呼び出し data <- p53DataSet #オブジェクト名の変更(dataとして取り扱う) rownames(data) <- toupper(rownames(data))#gene symbolを大文字に変換している(gmtファイルに合わせるため) dim(data) #確認してるだけです data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #GSAR本番(正確にはGSARから提供されているGSNCA法の実行) set.seed(1053) #おまじない(同じ乱数になるようにするため) hoge <- gmt[[param]] #解析したい遺伝子セット情報をhogeに格納 length(hoge) #遺伝子数を表示(gmtファイル) obj <- is.element(rownames(data), hoge)#条件判定 sum(obj) #遺伝子数を表示(発現データ中に存在するものに限定) p.value <- GSNCAtest(data[obj, ], data.cl)#GSNCAを実行 p.value #p-valueを表示 #ファイルに保存(相関ネットワーク(correlation network)図) png(out_f, pointsize=13, width=param_fig[1], height=param_fig[2])#出力ファイルの各種パラメータを指定 plotMST2.pathway(object=data[obj, ], #相関ネットワーク(correlation network)図の作成 group=data.cl, name=param, #相関ネットワーク(correlation network)図の作成 legend.size=1.2, leg.x=-1.2, #相関ネットワーク(correlation network)図の作成 leg.y=2, label.size=1, #相関ネットワーク(correlation network)図の作成 label.dist=0.8, cor.method="pearson")#相関ネットワーク(correlation network)図の作成 dev.off() #おまじない
4. GSARの解析例として示されているp53 datasetの場合:
gmtファイル中の遺伝子セット全体に対して、GSNCA法を遺伝子セットごとに適用するやり方です。 遺伝子セット中の遺伝子リストを発現データ中に含まれるものに限定したのち(前処理)、 遺伝子数が18以上40以下の遺伝子セットに限定して GSNCA法を適用しています。1,324遺伝子セットの計算で約80分。 実際の局面では、10以上500以下くらいでやるといいと思います(それでも約5000遺伝子セットで約2時間)。 出力結果はhoge4.txtと同じような感じになると思います。 1列目が遺伝子セット名、2列目が遺伝子数、3列目がGSNCA法実行結果のp-valueです。 尚、2列目の遺伝子数は、発現データ中に含まれる遺伝子セットを構成する遺伝子数であり、入力のgmtファイル中の遺伝子数と同じかそれよりも少ない数になります。
in_f <- "c2.all.v5.2.symbols.gmt" #入力ファイル名を指定してin_fに格納(gmtファイル) out_f <- "hoge4.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 17 #G1群のサンプル数を指定 param_G2 <- 33 #G2群のサンプル数を指定 param_min <- 18 #最小遺伝子数を指定 param_max <- 40 #最大遺伝子数を指定 #必要なパッケージをロード library(GSAR) #パッケージの読み込み library(GSA) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成 hoge <- GSA.read.gmt(in_f) #in_fで指定したファイルの読み込み(不完全な最終行が見つかりました、となっても気にしない) gmt <- hoge$genesets #フォーマット変換 names(gmt) <- hoge$geneset.names #フォーマット変換 data(p53DataSet) #GSARパッケージ中のp53DataSetオブジェクトの呼び出し data <- p53DataSet #オブジェクト名の変更(dataとして取り扱う) rownames(data) <- toupper(rownames(data))#gene symbolを大文字に変換している(gmtファイルに合わせるため) dim(data) #確認してるだけです data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #前処理(遺伝子セット中の遺伝子リストを発現データ中に含まれるものに限定) obj <- lapply(gmt, is.element, rownames(data))#発現データ中に含まれるgene symbolsをTRUE、そうでないものをFALSEとしている gmt2 <- list() #プレースホルダの作成(空のリストを作成してるだけ) for(i in 1:length(gmt)){ #遺伝子セットの数だけループを回す uge <- obj[[i]] #i番目の遺伝子セット中の発現データ中に含まれるか否かの論理値ベクトルをugeに格納 gmt2 <- append(gmt2, list(gmt[[i]][uge]))#gmt2に情報をどんどん追加 } #遺伝子セットの数だけループを回す names(gmt2) <- names(gmt) #gmtの遺伝子セット名情報をgmt2にコピー #GSAR本番(正確にはGSARから提供されているGSNCA法の実行) set.seed(1053) #おまじない(同じ乱数になるようにするため) p.value <- TestGeneSets(object=data, group=data.cl,#GSNCAを実行 geneSets=gmt2, min.size=param_min, #GSNCAを実行 max.size=param_max, test="GSNCAtest")#GSNCAを実行 #ファイルに保存 tmp <- cbind(names(p.value), sapply(gmt2[names(p.value)], length), p.value)#保存したい情報をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
5. サンプルデータ27の8,655 genes×50 samplesのアレイデータ(sample27.txt; 約7.3MB)の場合:
4.と基本的に同じで、発現データをファイルから読み込んでいるだけです。出力ファイルは、p-valueで昇順(低い -> 高い)にソートしています。 ファイル出力直前のソートは、このページの通常の書き方と異なっています。tmp[order(unlist(p.value)),]のunlist(p.value)の部分です。 このページでは通常tmp[order(tmp$p.value),]のようにtmp$p.valueのような書き方をしますが、これだとエラーが出るからです。 尚、5.と6.は同じ結果になりますが、計算時間は5.は約80分で6.は約40分と2倍ほど高速ですので6.のほうがおススメです。
in_f1 <- "sample27.txt" #入力ファイル名を指定してin_f1に格納(発現データ) in_f2 <- "c2.all.v5.2.symbols.gmt" #入力ファイル名を指定してin_f2に格納(gmtファイル) out_f <- "hoge5.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 17 #G1群のサンプル数を指定 param_G2 <- 33 #G2群のサンプル数を指定 param_min <- 18 #最小遺伝子数を指定 param_max <- 40 #最大遺伝子数を指定 #必要なパッケージをロード library(GSAR) #パッケージの読み込み library(GSA) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f1, header=TRUE, row.names=1, sep="\t", quote="")#in_f1で指定したファイルの読み込み rownames(data) <- toupper(rownames(data))#gene symbolを大文字に変換している(gmtファイルに合わせるため) data <- as.matrix(data) #型変換(TestGeneSets関数が要求しているため) dim(data) #確認してるだけです hoge <- GSA.read.gmt(in_f2) #in_f2で指定したファイルの読み込み(不完全な最終行が見つかりました、となっても気にしない) gmt <- hoge$genesets #フォーマット変換 names(gmt) <- hoge$geneset.names #フォーマット変換 data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #前処理(遺伝子セット中の遺伝子リストを発現データ中に含まれるものに限定) obj <- lapply(gmt, is.element, rownames(data))#発現データ中に含まれるgene symbolsをTRUE、そうでないものをFALSEとしている gmt2 <- list() #プレースホルダの作成(空のリストを作成してるだけ) for(i in 1:length(gmt)){ #遺伝子セットの数だけループを回す uge <- obj[[i]] #i番目の遺伝子セット中の発現データ中に含まれるか否かの論理値ベクトルをugeに格納 gmt2 <- append(gmt2, list(gmt[[i]][uge]))#gmt2に情報をどんどん追加 } #遺伝子セットの数だけループを回す names(gmt2) <- names(gmt) #gmtの遺伝子セット名情報をgmt2にコピー #GSAR本番(正確にはGSARから提供されているGSNCA法の実行) set.seed(1053) #おまじない(同じ乱数になるようにするため) p.value <- TestGeneSets(object=data, group=data.cl,#GSNCAを実行 geneSets=gmt2, min.size=param_min, #GSNCAを実行 max.size=param_max, test="GSNCAtest")#GSNCAを実行 #ファイルに保存 tmp <- cbind(names(p.value), sapply(gmt2[names(p.value)], length), p.value)#保存したい情報をtmpに格納 tmp <- tmp[order(unlist(p.value)), ] #p-value順にソートした結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
6. サンプルデータ27の8,655 genes×50 samplesのアレイデータ(sample27.txt; 約7.3MB)の場合:
5.と同じですが、遺伝子数が18以上40以下の遺伝子セットに限定するのを TestGeneSets関数を実行する前に独立にやっています。GSARのマニュアルとは異なりますが、6.のほうが高速です。
in_f1 <- "sample27.txt" #入力ファイル名を指定してin_f1に格納(発現データ) in_f2 <- "c2.all.v5.2.symbols.gmt" #入力ファイル名を指定してin_f2に格納(gmtファイル) out_f <- "hoge6.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 17 #G1群のサンプル数を指定 param_G2 <- 33 #G2群のサンプル数を指定 param_min <- 18 #最小遺伝子数を指定 param_max <- 40 #最大遺伝子数を指定 #必要なパッケージをロード library(GSAR) #パッケージの読み込み library(GSA) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f1, header=TRUE, row.names=1, sep="\t", quote="")#in_f1で指定したファイルの読み込み rownames(data) <- toupper(rownames(data))#gene symbolを大文字に変換している(gmtファイルに合わせるため) data <- as.matrix(data) #型変換(TestGeneSets関数が要求しているため) dim(data) #確認してるだけです hoge <- GSA.read.gmt(in_f2) #in_f2で指定したファイルの読み込み(不完全な最終行が見つかりました、となっても気にしない) gmt <- hoge$genesets #フォーマット変換 names(gmt) <- hoge$geneset.names #フォーマット変換 data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #前処理1(遺伝子セット中の遺伝子リストを発現データ中に含まれるものに限定) obj <- lapply(gmt, is.element, rownames(data))#発現データ中に含まれるgene symbolsをTRUE、そうでないものをFALSEとしている gmt2 <- list() #プレースホルダの作成(空のリストを作成してるだけ) for(i in 1:length(gmt)){ #遺伝子セットの数だけループを回す uge <- obj[[i]] #i番目の遺伝子セット中の発現データ中に含まれるか否かの論理値ベクトルをugeに格納 gmt2 <- append(gmt2, list(gmt[[i]][uge]))#gmt2に情報をどんどん追加 } #遺伝子セットの数だけループを回す names(gmt2) <- names(gmt) #gmtの遺伝子セット名情報をgmt2にコピー #前処理2(遺伝子数が指定した条件を満たす遺伝子セットに限定) obj <- (sapply(gmt2, length) >= param_min)#発現データ中に含まれるgene symbolsをTRUE、そうでないものをFALSEとしている gmt3 <- gmt2[obj] #プレースホルダの作成(空のリストを作成してるだけ) obj <- (sapply(gmt3, length) <= param_max)#発現データ中に含まれるgene symbolsをTRUE、そうでないものをFALSEとしている gmt3 <- gmt3[obj] #プレースホルダの作成(空のリストを作成してるだけ) length(gmt3) #確認してるだけです #GSAR本番(正確にはGSARから提供されているGSNCA法の実行) set.seed(1053) #おまじない(同じ乱数になるようにするため) p.value <- TestGeneSets(object=data, group=data.cl,#GSNCAを実行 geneSets=gmt2, min.size=param_min, #GSNCAを実行 max.size=param_max, test="GSNCAtest")#GSNCAを実行 #ファイルに保存 tmp <- cbind(names(p.value), sapply(gmt2[names(p.value)], length), p.value)#保存したい情報をtmpに格納 tmp <- tmp[order(unlist(p.value)), ] #p-value順にソートした結果をtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存
7. サンプルデータ27の8,655 genes×50 samplesのアレイデータ(sample27.txt; 約7.3MB)の場合:
3.と基本的に同じですが、発現データファイルを読み込ませている点が異なります。 また、set.seed(1053)として、乱数を発生させる際のタネ番号を3.と同じにしているので、結果が全く同じになるはずですが、 ネットワーク図が若干異なっている現象は確認済みです。どなたか理由が分かった方は教えてくださいm(_ _)m
in_f1 <- "sample27.txt" #入力ファイル名を指定してin_f1に格納(発現データ) in_f2 <- "c2.all.v5.2.symbols.gmt" #入力ファイル名を指定してin_f2に格納(gmtファイル) out_f <- "hoge7.png" #出力ファイル名を指定してout_fに格納 param_G1 <- 17 #G1群のサンプル数を指定 param_G2 <- 33 #G2群のサンプル数を指定 param <- "LU_TUMOR_VASCULATURE_UP" #解析したい遺伝子セット名を指定 param_fig <- c(700, 650) #ファイル出力時の横幅と縦幅を指定(単位はピクセル) #必要なパッケージをロード library(GSAR) #パッケージの読み込み library(GSA) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f1, header=TRUE, row.names=1, sep="\t", quote="")#in_f1で指定したファイルの読み込み rownames(data) <- toupper(rownames(data))#gene symbolを大文字に変換している(gmtファイルに合わせるため) data <- as.matrix(data) #型変換(TestGeneSets関数が要求しているため) dim(data) #確認してるだけです hoge <- GSA.read.gmt(in_f2) #in_f2で指定したファイルの読み込み(不完全な最終行が見つかりました、となっても気にしない) gmt <- hoge$genesets #フォーマット変換 names(gmt) <- hoge$geneset.names #フォーマット変換 data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #GSAR本番(正確にはGSARから提供されているGSNCA法の実行) set.seed(1053) #おまじない(同じ乱数になるようにするため) hoge <- gmt[[param]] #解析したい遺伝子セット情報をhogeに格納 length(hoge) #遺伝子数を表示(gmtファイル) obj <- is.element(rownames(data), hoge)#条件判定 sum(obj) #遺伝子数を表示(発現データ中に存在するものに限定) p.value <- GSNCAtest(data[obj, ], data.cl)#GSNCAを実行 p.value #p-valueを表示 #ファイルに保存(相関ネットワーク(correlation network)図) png(out_f, pointsize=13, width=param_fig[1], height=param_fig[2])#出力ファイルの各種パラメータを指定 plotMST2.pathway(object=data[obj, ], #相関ネットワーク(correlation network)図の作成 group=data.cl, name=param, #相関ネットワーク(correlation network)図の作成 legend.size=1.2, leg.x=-1.2, #相関ネットワーク(correlation network)図の作成 leg.y=2, label.size=1, #相関ネットワーク(correlation network)図の作成 label.dist=0.8, cor.method="pearson")#相関ネットワーク(correlation network)図の作成 dev.off() #おまじない
解析 | 機能解析 | パスウェイ(Pathway)解析 | Pathview (Luo_2013)
Pathviewパッケージを用いた解析のやり方を示します。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し以下をコピペ。
1. ...の場合:
library(Pathview) #パッケージの読み込み
解析 | 機能解析 | パスウェイ(Pathway)解析 | GAGE (Luo_2009)
gageパッケージを用いた解析のやり方を示します。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し以下をコピペ。
1. ...の場合:
library(gage) #パッケージの読み込み
解析 | 機能解析 | パスウェイ(Pathway)解析 | SPIA (Tarca_2009)
SPIAパッケージを用いた解析のやり方を示します。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し以下をコピペ。
1. ...の場合:
library(SPIA) #パッケージの読み込み
解析 | 機能解析 | パスウェイ(Pathway)解析 | GSA (Efron_2007)
GSAパッケージを用いた解析のやり方を示します。 オリジナルのprobeset IDからgene symbolにID変換がなされた発現データファイルを入力としています。 これは、「イントロ | アノテーション情報取得 | GEOquery(Davis_2007)」 で入手したprobeset IDとgene symbolの対応表のファイル、およびオリジナルのprobeset IDごとの発現データファイルを用いて 「前処理 | ID変換 | probe ID --> gene symbol」 でID変換したものです。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し以下をコピペ。
1.サンプルデータ20のdata_rma_2_nr_LIV.txtの場合:
肝臓のみからなる14,132 genes×8 samplesのデータです。LIV_fed vs. LIV_fastedの2群間比較です。
in_f1 <- "data_rma_2_nr_LIV.txt" #入力ファイル名を指定してin_f1に格納(発現データファイル) in_f2 <- "c2.cp.kegg.v5.0.symbols.gmt" #入力ファイル名を指定してin_f2に格納(gmtファイル) out_f1 <- "hoge1_G1.txt" #出力ファイル名を指定してout_f1に格納(G1群で高発現の遺伝子セットリスト) out_f2 <- "hoge1_G2.txt" #出力ファイル名を指定してout_f2に格納(G2群で高発現の遺伝子セットリスト) param_G1 <- 4 #G1群のサンプル数を指定 param_G2 <- 4 #G2群のサンプル数を指定 param_FDR <- 0.1 #false discovery rate (FDR)閾値を指定 #必要なパッケージをロード library(GSA) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成 gmt <- GSA.read.gmt(in_f2) #in_f2で指定したファイルの読み込み(不完全な最終行が見つかりました、となっても気にしない) data <- read.table(in_f1, header=TRUE, row.names=1, sep="\t", quote="")#in_f1で指定したファイルの読み込み rownames(data) <- toupper(rownames(data))#gene symbolを大文字に変換している(gmtファイルに合わせるため) data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #GSA本番 out <- GSA(data, data.cl, #GSAを実行し、結果をoutに格納 genesets=gmt$genesets, #GSAを実行し、結果をoutに格納 genenames=rownames(data), #GSAを実行し、結果をoutに格納 resp.type="Two class unpaired")#GSAを実行し、結果をoutに格納 tmp <- GSA.listsets(out, #param_FDRで指定したFDR閾値を満たす遺伝子セットのみリストアップした結果をtmpに格納 geneset.names=gmt$geneset.names,#param_FDRで指定したFDR閾値を満たす遺伝子セットのみリストアップした結果をtmpに格納 maxchar=max(nchar(gmt$geneset.names)),#param_FDRで指定したFDR閾値を満たす遺伝子セットのみリストアップした結果をtmpに格納 FDRcut=param_FDR) #param_FDRで指定したFDR閾値を満たす遺伝子セットのみリストアップした結果をtmpに格納 #ファイルに保存 write.table(tmp$negative, out_f1, sep="\t", append=F, quote=F, row.names=F)#tmp$negativeの中身を指定したファイル名で保存 write.table(tmp$positive, out_f2, sep="\t", append=F, quote=F, row.names=F)#tmp$positiveの中身を指定したファイル名で保存
2.サンプルデータ20のdata_rma_2_nr.txtの場合:
14,132 genes×24 samplesのデータです。 LIV_fed vs. LIV_fastedの2群間比較を行うべく、それらの位置情報を指定しています。
in_f1 <- "data_rma_2_nr.txt" #入力ファイル名を指定してin_f1に格納(発現データファイル) in_f2 <- "c2.cp.kegg.v5.0.symbols.gmt" #入力ファイル名を指定してin_f2に格納(gmtファイル) out_f1 <- "hoge2_G1.txt" #出力ファイル名を指定してout_f1に格納(G1群で高発現の遺伝子セットリスト) out_f2 <- "hoge2_G2.txt" #出力ファイル名を指定してout_f2に格納(G2群で高発現の遺伝子セットリスト) param_G1 <- 4 #G1群のサンプル数を指定 param_G2 <- 4 #G2群のサンプル数を指定 param_FDR <- 0.1 #false discovery rate (FDR)閾値を指定 param_posi <- c(17:20, 21:24) #G1群およびG2群の位置情報を指定 #必要なパッケージをロード library(GSA) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成、そしてサブセットの作成 gmt <- GSA.read.gmt(in_f2) #in_f2で指定したファイルの読み込み(不完全な最終行が見つかりました、となっても気にしない) data <- read.table(in_f1, header=TRUE, row.names=1, sep="\t", quote="")#in_f1で指定したファイルの読み込み rownames(data) <- toupper(rownames(data))#IDを大文字に変換している(gmtファイルに合わせるため) data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 data <- data[,param_posi] #サブセットを抽出 colnames(data) #確認してるだけです #GSA本番 out <- GSA(data, data.cl, #GSAを実行し、結果をoutに格納 genesets=gmt$genesets, #GSAを実行し、結果をoutに格納 genenames=rownames(data), #GSAを実行し、結果をoutに格納 resp.type="Two class unpaired")#GSAを実行し、結果をoutに格納 tmp <- GSA.listsets(out, #param_FDRで指定したFDR閾値を満たす遺伝子セットのみリストアップした結果をtmpに格納 geneset.names=gmt$geneset.names,#param_FDRで指定したFDR閾値を満たす遺伝子セットのみリストアップした結果をtmpに格納 maxchar=max(nchar(gmt$geneset.names)),#param_FDRで指定したFDR閾値を満たす遺伝子セットのみリストアップした結果をtmpに格納 FDRcut=param_FDR) #param_FDRで指定したFDR閾値を満たす遺伝子セットのみリストアップした結果をtmpに格納 #ファイルに保存 write.table(tmp$negative, out_f1, sep="\t", append=F, quote=F, row.names=F)#tmp$negativeの中身を指定したファイル名で保存 write.table(tmp$positive, out_f2, sep="\t", append=F, quote=F, row.names=F)#tmp$positiveの中身を指定したファイル名で保存
3.サンプルデータ20のdata_rma_2_nr.txtの場合:
14,132 genes×24 samplesのデータです。BAT_fed vs. BAT_fastedの2群間比較を行うべく、それらの位置情報を指定しています。
in_f1 <- "data_rma_2_nr.txt" #入力ファイル名を指定してin_f1に格納(発現データファイル) in_f2 <- "c2.cp.kegg.v5.0.symbols.gmt" #入力ファイル名を指定してin_f2に格納(gmtファイル) out_f1 <- "hoge3_G1.txt" #出力ファイル名を指定してout_f1に格納(G1群で高発現の遺伝子セットリスト) out_f2 <- "hoge3_G2.txt" #出力ファイル名を指定してout_f2に格納(G2群で高発現の遺伝子セットリスト) param_G1 <- 4 #G1群のサンプル数を指定 param_G2 <- 4 #G2群のサンプル数を指定 param_FDR <- 0.1 #false discovery rate (FDR)閾値を指定 param_posi <- c(1:4, 5:8) #G1群およびG2群の位置情報を指定 #必要なパッケージをロード library(GSA) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成、そしてサブセットの作成 gmt <- GSA.read.gmt(in_f2) #in_f2で指定したファイルの読み込み(不完全な最終行が見つかりました、となっても気にしない) data <- read.table(in_f1, header=TRUE, row.names=1, sep="\t", quote="")#in_f1で指定したファイルの読み込み rownames(data) <- toupper(rownames(data))#IDを大文字に変換している(gmtファイルに合わせるため) data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 data <- data[,param_posi] #サブセットを抽出 colnames(data) #確認してるだけです #GSA本番 out <- GSA(data, data.cl, #GSAを実行し、結果をoutに格納 genesets=gmt$genesets, #GSAを実行し、結果をoutに格納 genenames=rownames(data), #GSAを実行し、結果をoutに格納 resp.type="Two class unpaired")#GSAを実行し、結果をoutに格納 tmp <- GSA.listsets(out, #param_FDRで指定したFDR閾値を満たす遺伝子セットのみリストアップした結果をtmpに格納 geneset.names=gmt$geneset.names,#param_FDRで指定したFDR閾値を満たす遺伝子セットのみリストアップした結果をtmpに格納 maxchar=max(nchar(gmt$geneset.names)),#param_FDRで指定したFDR閾値を満たす遺伝子セットのみリストアップした結果をtmpに格納 FDRcut=param_FDR) #param_FDRで指定したFDR閾値を満たす遺伝子セットのみリストアップした結果をtmpに格納 #ファイルに保存 write.table(tmp$negative, out_f1, sep="\t", append=F, quote=F, row.names=F)#tmp$negativeの中身を指定したファイル名で保存 write.table(tmp$positive, out_f2, sep="\t", append=F, quote=F, row.names=F)#tmp$positiveの中身を指定したファイル名で保存
解析 | 機能解析 | パスウェイ(Pathway)解析 | sigPathway (Tian_2005)
sigPathwayパッケージを用いた解析のやり方を示します。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し以下をコピペ。
1. ...の場合:
library(sigPathway) #パッケージの読み込み
解析 | 機能解析(GSEA周辺)について(以下は再編予定)
記述内容が相当古くなっているため、再編予定です。。。
ある程度遺伝子機能が分かっている生物種に対して行う解析手段です。GSEAはGene Set Enrichment Analysisの略です。
基本的に”2群間比較データ”用の解析なのかも...。
例えば、従来の2群間比較(例. 癌 vs. 正常)のような場合で発現変動遺伝子を検出したい場合には、発現変動の度合いで全遺伝子をランキングし、FDRやp値の閾値を満たす上位x個を抽出してそれらがどのような機能をもつものが多いか(例えば「pathway関連遺伝子群が多い」など)などを調べて論文にしていました。
最近では、「代謝パスウェイに関連している遺伝子セット」や「同じGene Ontologyカテゴリに属する遺伝子セット」などが予め(a priori)分かっている場合が多いので、その情報を用いてFold changeやt統計量などの手段で発現変動の度合いで全遺伝子をランキングした結果に対して、例えば「代謝パスウェイに関連している遺伝子セット」が比較しているサンプル間で”動いている”かどうかを偏りの程度から判断するのがGSEA(遺伝子セットの濃縮度解析?!)の基本的な考え方です。
当然a priori defined setの偏りの程度を調べるための手段はいくらでも多くのやり方が考えられるので、GSEA法(Subramanian et al., PNAS, 2005)が出て以来、様々な改良版が報告されています。
実際、Rプログラムが提供されているものだけでも、以下の方法が提案されています:
- PAGE(Kim and Volsky, BMC Bioinformatics, 2005):この論文中に書かれている方法を門田が自作してみたもの。
- PGSEA(Kim and Volsky, BMC Bioinformatics, 2005):PAGEのR版だと書いてはいるが、原著論文に書かれているやり方とは違うと思います...。
- GSEA(Subramanian et al., PNAS, 2005):GSEAのR版ということだが、初心者には非常に扱いづらいので、JAVA版をお勧めします...。
- GSA(Efron and Tibshirani, Ann. Appl. Stat., 2007):20120612に一通り使えるようになりました。
他にも
- GeneTrail(Backes et al., NAR, 2007)
- Jiang and Gentlemanらによる拡張法 (Bioinformatics, 2007)
- SAM-GS (Dinu et al., BMC Bioinformatics, 2007)
- GSEA-P (Subramanian et al., Bioinformatics, 2007)
など様々な手法が提案されているようです。
これは、入力となる(log2変換後の)遺伝子発現データが与えられてから以下の多くのステップを経てGSEA系解析を行うわけですが、各ステップで様々な選択肢があるためです:
- step1(2群間比較用の様々な統計量の中から一つを選択;gene-level statistics)
- t統計量、WAD、SAM、Rank productsなど
- step2(得られた統計量の変換;transformation)
- 変換なし、統計量をrankに変換、統計量の絶対値に変換、統計量の二乗に変換など
- step3(遺伝子セットの統計量;gene-set statistics)
- (特定の遺伝子セットに含まれる遺伝子群の変換後の統計量の)平均(mean)、中央値(median)、Wilcoxonの順位和統計量、改良版Kolmogorov-Smirnov統計量など
- step4(帰無仮説;Null hypothesis)
-
- Q1(競合帰無仮説;competitive null hypothesis):「特定の遺伝子セットに含まれる遺伝子群のgene-set statistic」と「その遺伝子群の以外のgene-set statistic」は同じ
- Q1(完全帰無仮説;complete null hypothesis):「特定の遺伝子セットに含まれる遺伝子群のgene-set statistic」と「(その遺伝子群を含む)全遺伝子セットに含まれる遺伝子のgene-set statistic」は同じ
- Q2(自己充足型帰無仮説;self-contained null hypothesis):「特定の遺伝子セットに含まれる遺伝子群のgene-set statistic」と「sample label permutation(ランダムなラベル情報という意味)によって得られた特定の遺伝子セットに含まれる遺伝子群のgene-set statistic」は同じ
- Q2(グローバル帰無仮説;global null hypothesis):発現変動遺伝子はない、と仮定
この中で、特にstep2での選択は結果に大きな影響を与える(Ackermann and Strimmer, BMC Bioinformatics, 2009)ので違いをよく認識したうえで利用することをお勧めします。
例えばオリジナルのPAGE法(Kim_2005)は、「step1:AD統計量(Average Difference)、step2:変換なし、step3:mean、step4:Q1?!」ですので、
ある遺伝子セットに含まれる遺伝子メンバーの半分がG1群>>G2群、もう半分がG1群<<G2群(遺伝子セットAとする)だったとすると、step3でそれらのAD統計量の平均値を計算するとgene-set statisticは0付近の値をとることになります。
PAGE法ではこの平均値の絶対値が大きいものほど有意だと判定されるので、結果としてその遺伝子セットが明らかに2群間で変動していたとしてもその検出は原理的に不可能です。
ゆえに下記の三つのやり方はオリジナルのPAGE法(Kim_2005)に基づいたものなので、上記問題が起こりうることを認識したうえでご利用ください。
- PAGE法(Kim_2005)の考え方について
- PAGE法(Kim_2005;統計量の変換なし)を用いてGene Ontology解析
- PAGE法(Kim_2005;統計量の変換なし)を用いてPathway解析
ただし、上記のやり方は「遺伝子メンバーの半分がG1群>>G2群、もう半分がその逆」のような遺伝子セットAの検出はできないものの、全体としてG1群(あるいはG2群)で高発現側に偏っているような他の大部分の遺伝子セットは普通に検出できますし、そのような両方向でなく一方向。
遺伝子セットAのようなものも検出するための一つの手段としては、step2で「統計量の絶対値」あるいは「統計量の二乗」に変換することです。これの前者(統計量の絶対値)を実装したのが下記のものです。
2009/10/23現在、このページで最後まで解析ができるのはPAGE法(Kim_2005)のみです。
- PAGE法(Kim_2005;統計量の変換なし)の考え方についてでは、原著論文中で実際に解析したデータの追試を行うことで、解析の概略、結果の解釈の仕方などを述べています。
入力データは、前処理 | ID変換 | 同じ遺伝子名を持つものをまとめるを利用して得られた同じGene Symbolを持たない遺伝子発現データですのでご注意ください。
解析 | 機能解析 | PAGE法(Kim_2005;統計量の変換なし)の考え方について
PAGE法の参考文献1に書かれているPAGE法で遺伝子セット濃縮度解析(GSEA)解析を行うべく、解析の概略、結果の解釈の仕方などを述べます。
ここでは、 参考文献1のTable1で示された"OXPHOS_HG-U133A"という遺伝子セット(Gene set)のZ scoreの計算結果がどのようにして得られるのかを示します。
得られた結果は、若干原著論文(参考文献1)中のTable1の数値とは違いますが、これは参考文献2からとってきたOXPHOS_HG-U133A_probesの遺伝子リストを用いたためかもしれません。
つまり、原著論文では参考文献2から得られた遺伝子リストをそのまま使ったかどうかには言及していないために、その後アップデートされた遺伝子リストを使っていれば結果は異なりうるということです。ですので、細かい違いは気にしなくてもいいと思います。
ここでは、対数変換前のデータのダウンロードから、発現データファイル中の余分な行や列の除去、前処理や対数変換、サンプル名が長いので文字列の最初の1-8文字分のみをサンプル名とするなどの細かい作業をやってから
17 NGT samples vs. 18 DM2 samplesのPAGE解析を行っています。reannotate_select_cal.eis中のどの列が目的のサンプルに相当するかは、クラスラベル情報を含むファイル(Phenotype_Data.xls)から、全43サンプルのうち、「1-17列がNGTサンプル」、「26-43列がDM2サンプル」のデータであることが分かっているとします。
- 「参考文献1のTable1」の解析は参考文献2のデータについて行ったものです。
まずは必要な情報(発現情報や遺伝子セットの情報)をここからゲットします。- 発現データファイル(Human diabetes expression data)をダウンロード。
- クラスラベル情報を含むファイル(Phenotype data)をダウンロード。
- 遺伝子セット情報を含むファイル(Probe sets corresponding to gene sets)をダウンロード。
- ダウンロードした圧縮ファイルを解凍すると以下のファイルが得られます。
- 発現データファイル(reannotate_select_cal.eis; 対数変換されていないpreprocessing前のデータ)
- クラスラベル情報を含むファイル(Phenotype_Data.xls)
- 「all_pathways」というディレクトリ中にある”酸化的リン酸化に関係する遺伝子のリスト”ファイル(OXPHOS_HG-U133A_probes)
- 実際にRで読み込むのはreannotate_select_cal.eisとOXPHOS_HG-U133A_probesの二つ。
これをデスクトップなりどこか同じディレクトリ内に置く。 - Rを立ち上げ、読み込む二つのファイルを置いているディレクトリに移動し、以下をコピペ
in_f1 <- "reannotate_select_cal.eis" #入力ファイル名(発現データファイル)を指定してin_f1に格納 in_f2 <- "OXPHOS_HG-U133A_probes" #入力ファイル名(遺伝子リストファイル)を指定してin_f2に格納 param1 <- 1:17 #遺伝子発現行列中のG1群(NGTサンプルに相当)の位置(X-Y列)のXとYを指定 param2 <- 26:43 #遺伝子発現行列中のG2群(DM2サンプルに相当)の位置(X-Y列)のXとYを指定 param3 <- 1:8 #列名(サンプル名)の文字列のX-Y文字目のXとYを指定 #データファイルの読み込み data <- read.table(in_f1, header=TRUE, row.names=1, sep="\t", quote="")#in_f1で指定したファイルの読み込み data$NAME <- NULL #余分な列(NAMEという名前の列に相当)の削除 data <- data[-1,] #余分な行(EWEIGHTという名前の行に相当)の削除 #参考文献1に記載されている通りのデータの前処理(preprocessing)を実行 mean_value <- 1000 #各サンプルの平均発現強度を1000にすべく、mean_valueに格納 floor_value <- 100 #シグナル強度が100未満のものを100にすべく、floor_valueに格納 tmp_mean <- apply(data, 2, mean, na.rm=TRUE)#各サンプル(列)の平均シグナル強度を計算した結果をtmp_meanに格納 data.tmp <- sweep(data, 2, mean_value/tmp_mean, "*")#各列中の全てのシグナル値にmean_value/tmp_meanを掛け、その結果をdata.tmpに格納 data.tmp[data.tmp < floor_value] <- floor_value#シグナル強度がfloor_value未満のものをfloor_valueにする data.tmp <- log(data.tmp, base=2) #log(底は2)をとる rownames(data.tmp) <- rownames(data) #data_tmpの行の名前をdataの行の名前として利用する colnames(data.tmp) <- substr(colnames(data),param3[1],param3[length(param3)])#data_tmpの列の名前が長いのでparam3で指定した領域をdata.tmpの列の名前にする #全遺伝子(母集団)の倍率変化の平均(myu)と標準偏差(sigma)をまずは求める dim(data.tmp) #行数と列数を確認 logratio <- apply(data.tmp[,param2], 1, mean, na.rm=TRUE) - apply(data.tmp[,param1], 1, mean, na.rm=TRUE)#全遺伝子の倍率変化(DM2/NGT; logスケールデータなのでこの場合引き算となっている)を計算し、logratioに格納 mean_set <- mean(logratio) #全遺伝子の倍率変化の平均を計算し、mean_setに格納 sd_set <- sd(logratio) #全遺伝子の倍率変化の標準偏差を計算し、sd_setに格納 #"in_f2"で指定した中の遺伝子セット(標本)のみの倍率変化の平均(mean_sample)と遺伝子数(標本サイズ)nを求める probe_OXPHOS <- read.table(in_f2, row.names=1, quote="")#遺伝子リストファイルの読み込み mean_sample <- mean(logratio[rownames(probe_OXPHOS)])#rownames(probe_OXPHOS)で見られる遺伝子セットのみの倍率変化の平均を計算し、mean_sampleに格納 n <- nrow(probe_OXPHOS) #rownames(probe_OXPHOS)で見られる遺伝子数をnに格納 #Z-score算出式を参考にして、「mean_set, sd_set, mean_sample, n」をもとにZ-scoreおよびそのp値を求める zscore <- (mean_sample - mean_set)*sqrt(n)/sd_set#zscoreを計算 pvalue <- (1 - pnorm(abs(zscore)))*2 #pvalueを計算 zscore #zscoreを表示 pvalue #pvalueを表示
- PAGE法: Kim and Volsky, BMC Bioinformatics, 2005
- >GSEA法のpreliminary versionを提案した論文:
- Nakai et al., BBB, 2008
解析 | 機能解析 | PAGE法(Kim_2005;統計量の変換なし)を用いてGene Ontology解析
Nakai et al., BBB, 2008(「Affymetrix Rat Genome 230 2.0 Array」を利用)のデータを遺伝子名重複を前処理 | 同じ遺伝子名を持つものをまとめることにより排除して得られた「24 samples×14026 genesからなる遺伝子発現行列ファイルdata_GSE7623_rma_nr.txtを入力として、Gene Ontology解析を行う。
このときGSEAの開発者らが作成した様々な遺伝子セット情報を収めたMolecular Signatures Database (MSigDB)からダウンロードした.gmt形式ファイルを読み込んで解析を行います。
ちなみに、ここではlogratioをmean(B)-mean(A)で定義しているので、「logratioが正の値の遺伝子は、G2群で発現が上昇した」ということを意味するので、G2群で発現が上昇した遺伝子が多数を占める遺伝子セットのZスコア(hoge.txt中のz_page列に相当)は負の大きな値を示します。
注意点としては、「"Member_num_thischip"列の数値が10未満のものは怪しい」ので、できればリストからは除外しておいたほうがいいです。理由は、原著論文中にも書いていますが、この方法は中心極限定理 (母集団の分布がどんな分布であっても"ある遺伝子セットのメンバーのFold changeの平均(標本平均に相当)"と"チップ上の全遺伝子のFold changeの平均(母平均に相当)"の間の誤差はサンプルサイズ(その遺伝子セットのメンバー数に相当)を大きくしたときに近似的に正規分布に従うという定理)を論拠としており、 "Member_num_thischip(サンプルのサイズに相当)"があまりに小さいと正規分布に従うという前提が成り立たないためです。それで、原著論文では、「PAGE法を利用可能な最低限必要な遺伝子セットを構成するメンバー数(the minimal gene set size)は10程度必要だ。」としています。ここでは、混乱をきたさないように「"Member_num_thischip"列の数値が10未満のものは最初から排除」してもよかったのですが、 8 or 9個しかなくp値が非常に低い場合でも、その遺伝子セットが動いていないと言い切れるわけではないと思うので、一応全ての情報を出力するようにしています。したがって、"p_page"列(p値)で低い順にソートした結果を眺めるのを基本としつつも"Member_num_thischip"列の数値が小さいかどうかにも注意を払うことをお勧めします。
以下を実行すると、最もよく動いていたGene Ontology IDはGO:0006631であったことが分かります。
解析例で示す24 samples×14026 genesからなる遺伝子発現行列データ(data_GSE7623_rma_nr.txt)のサンプルラベル情報は以下の通りです。
ここではLIVサンプルの「fed vs. 24h-fasted」のGene Ontology解析を例示します。LIVのfedサンプル(G1群)は17-20列目、24h-fastedサンプル(G2群)は21-24列目のデータに相当します。
GSM184414-184417: Brown adipose tissue (BAT), fed GSM184418-184421: Brown adipose tissue (BAT), 24 h-fasted GSM184422-184425: White adipose tissue (WAT), fed GSM184426-184429: White adipose tissue (WAT), 24 h-fasted GSM184430-184433: Liver tissue (LIV), fed GSM184434-184437: Liver tissue (LIV), 24 h-fasted
- Molecular Signatures Database (MSigDB)の
「Registration」のページで登録し、遺伝子セットをダウンロード可能な状態にする。 - Molecular Signatures Database (MSigDB)の 「Download gene sets」の"Download"のところをクリックし、Loginページで登録したe-mail addressを入力。
- これでMSigDBのダウンロードページに行けるので、
とりあえず「c5: gene ontology gene sets」の「GO biological process gene sets file」を解析すべく、
c5.bp.v4.0.symbols.gmtファイルを(data_GSE7623_rma_nr.txtをダウンロードしたディレクトリと同じところに)ダウンロードする。 - Rを立ち上げ、読み込む二つのファイルを置いているディレクトリに移動し、以下をコピペ
in_f1 <- "data_GSE7623_rma_nr.txt" #入力ファイル名(発現データファイル)を指定してin_f1に格納 in_f2 <- "c5.bp.v4.0.symbols.gmt" #入力ファイル名(遺伝子セットファイル)を指定してin_f2に格納 param1 <- 17:20 #遺伝子発現行列中のG1群(fedサンプルに相当)の位置(X-Y列)のXとYを指定 param2 <- 21:24 #遺伝子発現行列中のG2群(24h-fastedサンプルに相当)の位置(X-Y列)のXとYを指定 out_f <- "hoge.txt" #出力ファイル名を指定してout_fに格納 #必要なパッケージをロード library(PGSEA) #PGSEAパッケージ(ライブラリ)の読み込み #データファイルの読み込み gmt <- readGmt(in_f2) #in_f2で指定したファイルの読み込み(不完全な最終行が見つかりました、となっても気にしない) data <- read.table(in_f1, header=TRUE, row.names=1, sep="\t", quote="")#in_f1で指定したファイルの読み込み colnames(data) #GSM184414-184437まで順番に並んでいることを確認してるだけです #Zスコアを算出する関数calc_zを作成 calc_z <- function(x, AD1, mean_set1, sd_set1){#Zスコアを算出する関数calc_zを作成 hoge <- (mean_set1 - mean(AD1[intersect(names(AD1), x)], na.rm=TRUE))*sqrt(length(intersect(names(AD1), x)))/sd_set1#Zスコアを算出する関数calc_zを作成 return(hoge) #Zスコアを算出する関数calc_zを作成 } #Zスコアを算出する関数calc_zを作成 #PAGE解析のメイン部分 AD <- apply(data[,param2], 1, mean, na.rm=TRUE) - apply(data[,param1], 1, mean, na.rm=TRUE)#全遺伝子の倍率変化(logなので引き算)を計算し、ADに格納 names(AD) <- toupper(names(AD)) #.gmtファイルは大文字の遺伝子名なのでnames(AD)でみられる遺伝子名も大文字に変換する mean_set <- mean(AD) #全遺伝子の倍率変化の平均を計算し、mean_setに格納 sd_set <- sd(AD) #全遺伝子の倍率変化の標準偏差を計算し、sd_setに格納 z_page <- NULL #おまじない for(i in 1:length(gmt)){ #length(gmt)回だけループを回す z_page <- c(z_page, calc_z(gmt[[i]]@ids, AD, mean_set, sd_set))#gmt[[i]]@idsで表されるi番目の遺伝子セットの遺伝子群のZスコアを計算し、z_pageに格納 } #length(gmt)回だけループを回す p_page <- (1 - pnorm(abs(z_page)))*2 #Zスコアに対応するp値を計算し、p_pageに格納 #結果をまとめてファイルに保存 out <- NULL #おまじない for(i in 1:length(gmt)){ #length(gmt)回だけループを回す Geneset_name <- gmt[[i]]@reference #遺伝子セット名をGeneset_nameに格納 GO_ID <- substring(gmt[[i]]@desc, 32, 41)#遺伝子セット名に対応するGene Ontology IDをGO_IDに格納 Member_num <- length(gmt[[i]]@ids) #各遺伝子セットを構成する遺伝子数をMember_numに格納 Member_num_thischip <- length(intersect(names(AD), gmt[[i]]@ids))#各遺伝子セットを構成する"このチップに搭載されている"遺伝子数をMember_num_thischipに格納 out <- rbind(out, c(Geneset_name, GO_ID, Member_num, Member_num_thischip))#Geneset_name, Member_num, Member_num_thischipの情報をoutに格納 } #length(gmt)回だけループを回す colnames(out) <- c("Geneset_name", "GO_ID", "Member_num", "Member_num_thischip")#列名を付与 #ファイルに保存 tmp <- cbind(out, z_page, p_page) #outの右側にPAGE解析結果のZスコアとp値を追加してtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存 #以下は(こんなこともできますという)おまけ #p値の低い順にソートした結果を得たい場合: out_f2 <- "hoge2.txt" #出力ファイル名を指定してout_f2に格納 tmp2 <- tmp[order(p_page),] #p値(p_page)でソートした結果をtmp2に格納 write.table(tmp2, out_f2, sep="\t", append=F, quote=F, row.names=F)#tmp2の中身を指定したファイル名で保存
解析 | 機能解析 | PAGE法(Kim_2005;統計量の変換あり)を用いてGene Ontology解析
Nakai et al., BBB, 2008(「Affymetrix Rat Genome 230 2.0 Array」を利用)のデータを遺伝子名重複を前処理 | ID変換 | 同じ遺伝子名を持つものをまとめることにより排除して得られた「24 samples×14026 genesからなる遺伝子発現行列ファイルdata_GSE7623_rma_nr.txtを入力として、Gene Ontology解析を行う。
このときGSEAの開発者らが作成した様々な遺伝子セット情報を収めたMolecular Signatures Database (MSigDB)からダウンロードした.gmt形式ファイルを読み込んで解析を行います。
以下を実行すると、最もよく動いていたGene Ontology IDはGO:0006805であったことが分かりますが、この遺伝子セットを構成する遺伝子数は11個でそのうちこのチップ(Affymetrix Rat Genome 230 2.0 Array)に搭載されているのは4個しかないことが分かります。
PAGE法(Kim_2005;統計量の変換なし)を用いてGene Ontology解析に書いているように、"Member_num_thischip"列の数値(この場合4)があまりに少ないと偶然に有意であると判断される可能性が上昇しますので、XENOBIOTIC_METABOLIC_PROCESSが動いたと判断するのはまずいと思います。
また、統計量の変換(この場合AD統計量の”絶対値”を採用しているということ)を行っており、Z検定も行っていないので、もはやPAGE法とはいえないと思います...。
解析例で示す24 samples×14026 genesからなる遺伝子発現行列データ(data_GSE7623_rma_nr.txt)のサンプルラベル情報は以下の通りです。
ここではLIVサンプルの「fed vs. 24h-fasted」のGene Ontology解析を例示します。LIVのfedサンプル(G1群)は17-20列目、24h-fastedサンプル(G2群)は21-24列目のデータに相当します。
GSM184414-184417: Brown adipose tissue (BAT), fed GSM184418-184421: Brown adipose tissue (BAT), 24 h-fasted GSM184422-184425: White adipose tissue (WAT), fed GSM184426-184429: White adipose tissue (WAT), 24 h-fasted GSM184430-184433: Liver tissue (LIV), fed GSM184434-184437: Liver tissue (LIV), 24 h-fasted
- Molecular Signatures Database (MSigDB)の
「Registration」のページで登録し、遺伝子セットをダウンロード可能な状態にする。 - Molecular Signatures Database (MSigDB)の
「Download gene sets」の"Download"のところをクリックし、Loginページで登録したe-mail addressを入力。 - これでMSigDBのダウンロードページに行けるので、
とりあえず「c5: gene ontology gene sets」の「GO biological process gene sets file」を解析すべく、
c5.bp.v4.0.symbols.gmtファイルを(data_GSE7623_rma_nr.txtをダウンロードしたディレクトリと同じところに)ダウンロードする。 - Rを立ち上げ、読み込む二つのファイルを置いているディレクトリに移動し、以下をコピペ
in_f1 <- "data_GSE7623_rma_nr.txt" #入力ファイル名(発現データファイル)を指定してin_f1に格納 in_f2 <- "c5.bp.v4.0.symbols.gmt" #入力ファイル名(遺伝子セットファイル)を指定してin_f2に格納 param1 <- 17:20 #遺伝子発現行列中のG1群(fedサンプルに相当)の位置(X-Y列)のXとYを指定 param2 <- 21:24 #遺伝子発現行列中のG2群(24h-fastedサンプルに相当)の位置(X-Y列)のXとYを指定 out_f <- "hoge.txt" #出力ファイル名を指定してout_fに格納 #必要なパッケージをロード library(PGSEA) #PGSEAパッケージ(ライブラリ)の読み込み #データファイルの読み込み gmt <- readGmt(in_f2) #in_f2で指定したファイルの読み込み(不完全な最終行が見つかりました、となっても気にしない) data <- read.table(in_f1, header=TRUE, row.names=1, sep="\t", quote="")#in_f1で指定したファイルの読み込み colnames(data) #GSM184414-184437まで順番に並んでいることを確認してるだけです #PAGE解析のメイン部分 AD <- apply(data[,param2], 1, mean, na.rm=TRUE) - apply(data[,param1], 1, mean, na.rm=TRUE)#全遺伝子の倍率変化(logなので引き算)を計算し、ADに格納 names(AD) <- toupper(names(AD)) #.gmtファイルは大文字の遺伝子名なのでnames(AD)でみられる遺伝子名も大文字に変換する stat_page <- NULL #おまじない for(i in 1:length(gmt)){ #length(gmt)回だけループを回す genenames <- intersect(names(AD), gmt[[i]]@ids)#i番目の遺伝子セット中の遺伝子リストの中からチップに搭載されている遺伝子のみのGene symbolsをgenenamesに格納 stat_page <- c(stat_page, mean(abs(AD[genenames])))#genenamesで表された遺伝子リストのAD統計量の絶対値の平均を計算し、stat_pageに格納 } #length(gmt)回だけループを回す #結果をまとめてファイルに保存 out <- NULL #おまじない for(i in 1:length(gmt)){ #length(gmt)回だけループを回す Geneset_name <- gmt[[i]]@reference #遺伝子セット名をGeneset_nameに格納 GO_ID <- substring(gmt[[i]]@desc, 32, 41)#遺伝子セット名に対応するGene Ontology IDをGO_IDに格納 Member_num <- length(gmt[[i]]@ids) #各遺伝子セットを構成する遺伝子数をMember_numに格納 Member_num_thischip <- length(intersect(names(AD), gmt[[i]]@ids))#各遺伝子セットを構成する"このチップに搭載されている"遺伝子数をMember_num_thischipに格納 out <- rbind(out, c(Geneset_name, GO_ID, Member_num, Member_num_thischip))#Geneset_name, Member_num, Member_num_thischipの情報をoutに格納 } #length(gmt)回だけループを回す colnames(out) <- c("Geneset_name", "GO_ID", "Member_num", "Member_num_thischip")#列名を付与 #ファイルに保存 tmp <- cbind(out, stat_page) #outの右側にPAGE解析結果のAD統計量の絶対値の平均を追加してtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存 #以下は(こんなこともできますという)おまけ #AD統計量の絶対値の平均が高い順にソートした結果を得たい場合: out_f2 <- "hoge2.txt" #出力ファイル名を指定してout_f2に格納 tmp2 <- tmp[order(-stat_page),] #stat_pageでソートした結果をtmp2に格納 write.table(tmp2, out_f2, sep="\t", append=F, quote=F, row.names=F)#tmp2の中身を指定したファイル名で保存
解析 | 機能解析 | PAGE法(Kim_2005)を用いてGene Ontology解析した結果をQuickGOにかける
PAGE法(Kim_2005)を用いてGene Ontology解析では、hoge.txtをエクセルなどで開き、どのGene Ontology IDのものが動いたかをp値でソートすることによりTableを作成することまでが可能です。
解析例(LIVサンプルの「fed vs. 24h-fasted」のGene Ontology解析)で得られた上位10個の結果は以下の通りです。
Geneset_name GO_ID Member_num Member_num_thischip z_page p_page FATTY_ACID_METABOLIC_PROCESS GO:0006631 63 52 -7.799532229 6.22E-15 FATTY_ACID_BETA_OXIDATION GO:0006635 11 11 -6.203282697 5.53E-10 CELLULAR_RESPONSE_TO_NUTRIENT_LEVELS GO:0031669 10 10 6.154781714 7.52E-10 CELLULAR_RESPONSE_TO_STRESS GO:0033554 10 10 5.904066843 3.55E-09 CELLULAR_RESPONSE_TO_EXTRACELLULAR_STIMULUS GO:0031668 12 12 5.594950084 2.21E-08 FATTY_ACID_OXIDATION GO:0019395 18 18 -5.167180532 2.38E-07 MONOCARBOXYLIC_ACID_METABOLIC_PROCESS GO:0032787 88 75 -4.879088895 1.07E-06 BIOSYNTHETIC_PROCESS GO:0009058 470 383 4.869245113 1.12E-06 CELLULAR_BIOSYNTHETIC_PROCESS GO:0044249 321 265 4.577997388 4.69E-06 RESPONSE_TO_NUTRIENT_LEVELS GO:0031667 29 29 4.487353561 7.21E-06
この結果から、Zスコアの低い4つ(G2群で発現が上昇した遺伝子が多数を占める遺伝子セットを意味する)は"FATTY_ACID"や"METABOLIC"などの記述がかぶっているので、
Gene Ontology階層構造の親子関係になっていることが想像できます。この親子関係になっている様子を図で表したいときに以下を行います。
- エクセルで開いたhoge.txtをp値の低い順にソートして得られた状態で、上位10個のGene Ontology IDsに相当するセルをコピー
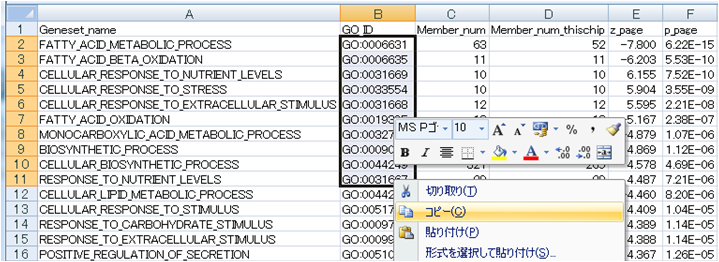
- QuickGOのウェブページを開き、「Your selection (0 terms)」の部分をクリック
もし「Your selection (0 terms)」となってない場合は「Empty」の部分をクリックして、以前の作業で残っていた情報を消す
- 四角のボックス部分に1.でコピーしておいたGO IDsをペーストし、「Add」ボタンを押す
「Your selection (0 terms)」だったのが、「Your selection (10 terms)」となります
- 「Your selection (10 terms)」の部分をクリックして、「View selected terms」をクリック
- 「Select all」の部分をクリックし、「chart」をクリック
- 以下のようなチャート図が得られるので、図上を右クリックで「名前を付けて画像を保存」とすれば図の完成です
解析 | 機能解析 | PAGE法(Kim_2005;統計量の変換なし)を用いてPathway解析
PAGE法を用いて、どのパスウェイが動いていたかを調べたいときに用います。
前処理 | フィルタリング | NAを含むものを除去の4を適用することによって得られた、各群で少なくとも一つ以上の数値の要素を含むものの、
NAやNaNの要素を含むsample13_7vs7_nr2.txtのようなAgilent two-colorデータの解析例を示します。
この例では、GSEAの開発者らが作成した様々な遺伝子セット情報を収めたMolecular Signatures Database (MSigDB)からダウンロードしたKEGG gene sets fileファイル(c2.kegg.v4.0.symbols.gmt)を読み込んで解析を行います。
この例で示す遺伝子発現行列データ(sample13_7vs7_nr2.txt)のサンプルラベル情報は「最初の7 samplesが面白い話を聞いた患者(G1群)で、残りの7 samplesが退屈な講義を聞いた患者(G2群)」です。
ちなみに、ここではlogratioをmean(B)-mean(A)で定義しているので、「logratioが正の値の遺伝子は、面白い話(A)を聞いたときに発現が減少し、退屈な話(B)を聞いて発現が上昇した」ということを意味します。よって、logratio > 0を満たす遺伝子が多数を占める遺伝子セットのZスコア(hoge.txt中のz_page列に相当)は負の大きな値を示します。
得られたhoge.txtファイルをエクセルなどで開き、"p_page"列(p値)で低い順にソートすれば、「G1群 vs. G2群」の二つの状態間で”動いているパスウェイ”順にソートされたことになる。論文の表とかで示す場合には「p値 < 0.05を満たすものだけ」とか「上位10個だけ」を表示することになります。
注意点としては、「"Member_num_thischip"列の数値が10未満のものは怪しい」ので、できればリストからは除外しておいたほうがいいです。理由は、原著論文中にも書いていますが、この方法は中心極限定理
(母集団の分布がどんな分布であっても"ある遺伝子セットのメンバーのFold changeの平均(標本平均に相当)"と"チップ上の全遺伝子のFold changeの平均(母平均に相当)"の間の誤差はサンプルサイズ(その遺伝子セットのメンバー数に相当)を大きくしたときに近似的に正規分布に従うという定理)を論拠としており、"Member_num_thischip(サンプルのサイズに相当)"があまりに小さいと正規分布に従うという前提が成り立たないためです。
それで、原著論文では、「PAGE法を利用可能な最低限必要な遺伝子セットを構成するメンバー数(the minimal gene set size)は10程度必要だ。」としています。ここでは、混乱をきたさないように「"Member_num_thischip"列の数値が10未満のものは最初から排除」してもよかったのですが、8 or 9個しかなくp値が非常に低い場合でも、そのパスウェイが動いていないと言い切れるわけではないと思うので、一応全ての情報を出力するようにしています。
したがって、"p_page"列(p値)で低い順にソートした結果を眺めるのを基本としつつも"Member_num_thischip"列の数値が小さいかどうかにも注意を払うことをお勧めします。
解析例を行って得られたhoge.txtの10未満しかないがp値がそこそこ低いものの一例としては、28番目の"HSA00791_ATRAZINE_DEGRADATION"です。
- Molecular Signatures Database (MSigDB)の
「Registration」のページで登録し、遺伝子セットをダウンロード可能な状態にする。 - Molecular Signatures Database (MSigDB)の
「Download gene sets」の"Download"のところをクリックし、Loginページで登録したe-mail addressを入力。 - これでMSigDBのダウンロードページに行けるので、
とりあえず「c2: curated gene sets」の「KEGG gene sets file」を解析すべく、
c2.kegg.v4.0.symbols.gmtファイルを(sample13_7vs7_nr.txtをダウンロードしたディレクトリと同じところに)ダウンロードする。 - Rを立ち上げ、読み込む二つのファイルを置いているディレクトリに移動し、以下をコピペ
in_f1 <- "sample13_7vs7_nr2.txt" #入力ファイル名(発現データファイル)を指定してin_f1に格納 in_f2 <- "c2.kegg.v4.0.symbols.gmt" #入力ファイル名(遺伝子セットファイル)を指定してin_f2に格納 out_f <- "hoge.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 7 #G1群のサンプル数を指定 param_G2 <- 7 #G2群のサンプル数を指定 #必要なパッケージをロード library(PGSEA) #PGSEAパッケージ(ライブラリ)の読み込み #入力ファイルの読み込みとラベル情報の作成 gmt <- readGmt(in_f2) #in_f2で指定したファイルの読み込み(不完全な最終行が見つかりました、となっても気にしない) data <- read.table(in_f1, header=TRUE, row.names=1, sep="\t", quote="")#in_f1で指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #Zスコアを算出する関数calc_zを作成 calc_z <- function(x, AD1, mean_set1, sd_set1){#Zスコアを算出する関数calc_zを作成 hoge <- (mean_set1 - mean(AD1[intersect(names(AD1), x)], na.rm=TRUE))*sqrt(length(intersect(names(AD1), x)))/sd_set1#Zスコアを算出する関数calc_zを作成 return(hoge) #Zスコアを算出する関数calc_zを作成 } #Zスコアを算出する関数calc_zを作成 #PAGE解析のメイン部分 AD <- apply(data[,data.cl == 2], 1, mean, na.rm=TRUE) - apply(data[,data.cl == 1], 1, mean, na.rm=TRUE)#全遺伝子の倍率変化(logなので引き算)を計算し、ADに格納 names(AD) <- toupper(names(AD)) #.gmtファイルは大文字の遺伝子名なのでnames(AD)でみられる遺伝子名も大文字に変換する mean_set <- mean(AD) #全遺伝子の倍率変化の平均を計算し、mean_setに格納 sd_set <- sd(AD) #全遺伝子の倍率変化の標準偏差を計算し、sd_setに格納 z_page <- NULL #おまじない for(i in 1:length(gmt)){ #length(gmt)回だけループを回す z_page <- c(z_page, calc_z(gmt[[i]]@ids, AD, mean_set, sd_set))#gmt[[i]]@idsで表されるi番目の遺伝子セットの遺伝子群のZスコアを計算し、z_pageに格納 } #length(gmt)回だけループを回す p_page <- (1 - pnorm(abs(z_page)))*2 #Zスコアに対応するp値を計算し、p_pageに格納 #結果をまとめてファイルに保存 out <- NULL #おまじない for(i in 1:length(gmt)){ #length(gmt)回だけループを回す Geneset_name <- gmt[[i]]@reference #遺伝子セット名をGeneset_nameに格納 Member_num <- length(gmt[[i]]@ids) #各遺伝子セットを構成する遺伝子数をMember_numに格納 Member_num_thischip <- length(intersect(names(AD), gmt[[i]]@ids))#各遺伝子セットを構成する"このチップに搭載されている"遺伝子数をMember_num_thischipに格納 out <- rbind(out, c(Geneset_name, Member_num, Member_num_thischip))#Geneset_name, Member_num, Member_num_thischipの情報をoutに格納 } #length(gmt)回だけループを回す colnames(out) <- c("Geneset_name", "Member_num", "Member_num_thischip")#列名を付与 #ファイルに保存 tmp <- cbind(out, z_page, p_page) #outの右側にPAGE解析結果のZスコアとp値を追加してtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存 #以下は(こんなこともできますという)おまけ #p値の低い順にソートした結果を得たい場合: out_f2 <- "hoge2.txt" #出力ファイル名を指定してout_f2に格納 tmp2 <- tmp[order(p_page),] #p値(p_page)でソートした結果をtmp2に格納 write.table(tmp2, out_f2, sep="\t", append=F, quote=F, row.names=F)#tmp2の中身を指定したファイル名で保存
解析 | 機能解析 | PAGE法(Kim_2005;統計量の変換あり)を用いてPathway解析
PAGE法を用いて、どのパスウェイが動いていたかを調べたいときに用います。
前処理 | フィルタリング | NAを含むものを除去の4を適用することによって得られた、各群で少なくとも一つ以上の数値の要素を含むものの、
NAやNaNの要素を含むsample13_7vs7_nr2.txtのようなAgilent two-colorデータの解析例を示します。
この例では、GSEAの開発者らが作成した様々な遺伝子セット情報を収めたMolecular Signatures Database (MSigDB)からダウンロードしたKEGG gene sets fileファイル(c2.kegg.v4.0.symbols.gmt)を読み込んで解析を行います。
この例で示す遺伝子発現行列データ(sample13_7vs7_nr2.txt)のサンプルラベル情報は「最初の7 samplesが面白い話を聞いた患者(G1群)で、残りの7 samplesが退屈な講義を聞いた患者(G2群)」です。
ちなみに、ここではAD統計量をmean(B)-mean(A)で定義しているので、「ADが正の値の遺伝子は、面白い話(A)を聞いたときに発現が減少し、退屈な話(B)を聞いて発現が上昇した」ということを意味します。。得られたhoge2.txtファイルは、「G1群 vs. G2群」の二つの状態間で”動いているパスウェイ”順にソートされた結果です。この場合、論文の表とかで示す場合には「上位10個だけ」などを表示することになります。
注意点としては、「"Member_num_thischip"列の数値が10未満のものは怪しい」ので、できればリストからは除外しておいたほうがいいです。一般的にメンバー数が10以上とか15以上の遺伝子セットのみ解析というのが多いというのも理由の一つです。例えば参考文献2では、メンバー数が15-500 genesの範囲の遺伝子セットのみを解析対象としています。
- Molecular Signatures Database (MSigDB)の
「Registration」のページで登録し、遺伝子セットをダウンロード可能な状態にする。 - Molecular Signatures Database (MSigDB)の
「Download gene sets」の"Download"のところをクリックし、Loginページで登録したe-mail addressを入力。 - これでMSigDBのダウンロードページに行けるので、
とりあえず「c2: curated gene sets」の「KEGG gene sets file」を解析すべく、
c2.kegg.v4.0.symbols.gmtファイルを(sample13_7vs7_nr.txtをダウンロードしたディレクトリと同じところに)ダウンロードする。 - Rを立ち上げ、読み込む二つのファイルを置いているディレクトリに移動し、以下をコピペ
in_f1 <- "sample13_7vs7_nr2.txt" #入力ファイル名(発現データファイル)を指定してin_f1に格納 in_f2 <- "c2.kegg.v4.0.symbols.gmt" #入力ファイル名(遺伝子セットファイル)を指定してin_f2に格納 out_f <- "hoge.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 7 #G1群のサンプル数を指定 param_G2 <- 7 #G2群のサンプル数を指定 #必要なパッケージをロード library(PGSEA) #PGSEAパッケージ(ライブラリ)の読み込み #入力ファイルの読み込みとラベル情報の作成 gmt <- readGmt(in_f2) #in_f2で指定したファイルの読み込み(不完全な最終行が見つかりました、となっても気にしない) data <- read.table(in_f1, header=TRUE, row.names=1, sep="\t", quote="")#in_f2で指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #AD統計量を計算 AD <- apply(data[,data.cl == 2], 1, mean, na.rm=TRUE) - apply(data[,data.cl == 1], 1, mean, na.rm=TRUE)#全遺伝子の倍率変化(logなので引き算)を計算し、ADに格納 names(AD) <- toupper(names(AD)) #.gmtファイルは大文字の遺伝子名なのでnames(AD)でみられる遺伝子名も大文字に変換する stat_page <- NULL #おまじない for(i in 1:length(gmt)){ #length(gmt)回だけループを回す genenames <- intersect(names(AD), gmt[[i]]@ids)#i番目の遺伝子セット中の遺伝子リストの中からチップに搭載されている遺伝子のみのGene symbolsをgenenamesに格納 stat_page <- c(stat_page, mean(abs(AD[genenames])))#genenamesで表された遺伝子リストのAD統計量の絶対値の平均を計算し、stat_pageに格納 } #length(gmt)回だけループを回す #結果をまとめてファイルに保存 out <- NULL #おまじない for(i in 1:length(gmt)){ #length(gmt)回だけループを回す Geneset_name <- gmt[[i]]@reference #遺伝子セット名をGeneset_nameに格納 Member_num <- length(gmt[[i]]@ids) #各遺伝子セットを構成する遺伝子数をMember_numに格納 Member_num_thischip <- length(intersect(names(AD), gmt[[i]]@ids))#各遺伝子セットを構成する"このチップに搭載されている"遺伝子数をMember_num_thischipに格納 out <- rbind(out, c(Geneset_name, Member_num, Member_num_thischip))#Geneset_name, Member_num, Member_num_thischipの情報をoutに格納 } #length(gmt)回だけループを回す colnames(out) <- c("Geneset_name", "Member_num", "Member_num_thischip")#列名を付与 #ファイルに保存 tmp <- cbind(out, stat_page) #outの右側にPAGE解析結果のAD統計量の絶対値の平均を追加してtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存 #以下は(こんなこともできますという)おまけ #AD統計量の絶対値の平均が高い順にソートした結果を得たい場合: out_f2 <- "hoge2.txt" #出力ファイル名を指定してout_f2に格納 tmp2 <- tmp[order(-stat_page),] #stat_pageでソートした結果をtmp2に格納 write.table(tmp2, out_f2, sep="\t", append=F, quote=F, row.names=F)#tmp2の中身を指定したファイル名で保存
解析 | 機能解析 | PAGE法(Kim_2005)を用いてPathway解析した後
まだ作成途中です...
PAGE法(Kim_2005;統計量の変換なし)を用いてPathway解析では、hoge2.txtをエクセルなどで開き、動いたKEGG Pathwayの上位10個やp値<0.01のものなどをリストアップすることまでが可能です。
解析例(「面白い話(A) vs. 退屈な話(B)」のPathway解析)で得られた上位10個の結果は以下の通りです。
Geneset_name Member_num Member_num_thischip z_page p_page HSA04612_ANTIGEN_PROCESSING_AND_PRESENTATION 83 75 -7.417644043 1.19E-13 HSA04650_NATURAL_KILLER_CELL_MEDIATED_CYTOTOXICITY 132 120 -6.455612947 1.08E-10 HSA04660_T_CELL_RECEPTOR_SIGNALING_PATHWAY 93 85 -6.10536501 1.03E-09 HSA04940_TYPE_I_DIABETES_MELLITUS 45 41 -5.127354084 2.94E-07 HSA05221_ACUTE_MYELOID_LEUKEMIA 53 49 -5.043817499 4.56E-07 HSA04720_LONG_TERM_POTENTIATION 69 67 -4.934603559 8.03E-07 HSA04540_GAP_JUNCTION 98 80 -4.240373448 2.23E-05 HSA05220_CHRONIC_MYELOID_LEUKEMIA 76 71 -4.047010307 5.19E-05 HSA04912_GNRH_SIGNALING_PATHWAY 97 93 -3.984577112 6.76E-05 HSA04810_REGULATION_OF_ACTIN_CYTOSKELETON 212 185 -3.852884301 0.000116735
この結果から、最も比較した2群間で動いているパスウェイは「HSA04612_ANTIGEN_PROCESSING_AND_PRESENTATION」であり、 遺伝子発現データ取得に用いたチップ上には75個の遺伝子が搭載されていることが分かりますが、 そのパスウェイ構成メンバーのどの遺伝子の発現がどちら向き(G1群 > G2群 or G1群 < G2群)に変化したのかまでをパスウェイ上に色でマップしたいときに以下を行います。
1. 知りたいパスウェイIDHSA04612を構成する遺伝子セットのAD統計量情報から対応する色の16進数値を入手すべく、以下をコピペ
- AD統計量が負の値のもの(G1群で発現上昇)を水色、AD統計量が正の値のもの(G2群で発現上昇)をピンク色で図示したい場合
param <- "HSA04612" #解析したいパスウェイIDを指定 param1 <- "#FF00FF" #AD > 0(G2群で発現上昇)のものの色(ピンク色)を指定 param2 <- "#0099FF" #AD < 0(G1群で発現上昇)のものの色(水色)を指定 out_f3 <- "hoge_detail.txt" #元となるAD統計量情報を含む出力ファイル名を指定してout_f3に格納 out_f4 <- "hoge_kegg.txt" #KEGG Pathway用出力ファイル名を指定してout_f4に格納 calc_color <- function(x){ #AD統計量から色の16進数値を返す関数calc_colorを作成 if(x > 0){ tmp_color <- param1 } #AD統計量>0のときはparam1で指定した色を返すべくtmp_colorに格納 if(x < 0){ tmp_color <- param2 } #AD統計量<0のときはparam2で指定した色を返すべくtmp_colorに格納 return(tmp_color) #tmp_colorの中身を結果として返す } #AD統計量から色の16進数値を返す関数calc_colorを作成 posi <- pmatch(param, tmp[,1]) #paramで指定したパスウェイIDのgmtファイル中での位置を同定しposiに格納 genenames <- intersect(names(AD), gmt[[posi]]@ids)#チップに搭載されている遺伝子のGene symbolsをgenenamesに格納 tmpAD <- AD[genenames] out <- apply(as.matrix(tmpAD), 1, calc_color) tmp3 <- cbind(genenames, tmpAD) #genenamesの右側にAD統計量情報を追加してtmp3に格納 write.table(tmp3, out_f3, sep="\t", append=F, quote=F, row.names=F, col.names=F)#tmpの中身を指定したファイル名で保存 tmp4 <- cbind(genenames, out) #genenamesの右側に色の16進数値情報を追加してtmp4に格納 write.table(tmp4, out_f4, sep=" ", append=F, quote=F, row.names=F, col.names=F)#tmpの中身を指定したファイル名で保存
- 上記の色使いを基本としつつ、AD <= -1を水色、-1 < AD < 0を薄水色、0 < AD < 1を薄ピンク色、AD >= 1をピンク色の4諧調で図示したい場合
(ちなみにAD統計量は「log2 scaleでの各群の算術平均値の差」なので、
AD <= -1は「G1群で2倍以上発現上昇」に相当し、AD >= 1は「G2群で2倍以上発現上昇」に相当します。)
param <- "HSA04612" #解析したいパスウェイIDを指定 param1 <- "#FF00FF" #AD >= 1(G2群で2倍以上発現上昇)のものの色(ピンク色)を指定 param2 <- "#FFCCFF" #0 < AD < 1(G2群で2倍未満発現上昇)のものの色(薄ピンク色)を指定 param3 <- "#CCFFFF" #-1 < AD < 0(G1群で2倍未満発現上昇)のものの色(薄水色)を指定 param4 <- "#0099FF" #AD <= -1(G1群で2倍以上発現上昇)のものの色(水色)を指定 out_f3 <- "hoge_detail.txt" #元となるAD統計量情報を含む出力ファイル名を指定してout_f3に格納 out_f4 <- "hoge_kegg.txt" #KEGG Pathway用出力ファイル名を指定してout_f4に格納 calc_color <- function(x){ #AD統計量から色の16進数値を返す関数calc_colorを作成 if(x >= 1){ tmp_color <- param1 } #AD >= 1のときはparam1で指定した色を返すべくtmp_colorに格納 if((0 < x) & (x < 1)){ tmp_color <- param2 }#0 < AD < 1のときはparam2で指定した色を返すべくtmp_colorに格納 if((-1 < x) & (x < 0)){ tmp_color <- param3 }#-1 < AD < 0のときはparam3で指定した色を返すべくtmp_colorに格納 if(x <= -1){ tmp_color <- param4 } #AD <= -1のときはparam4で指定した色を返すべくtmp_colorに格納 return(tmp_color) #tmp_colorの中身を結果として返す } #AD統計量から色の16進数値を返す関数calc_colorを作成 posi <- pmatch(param, tmp[,1]) #paramで指定したパスウェイIDのgmtファイル中での位置を同定しposiに格納 genenames <- intersect(names(AD), gmt[[posi]]@ids)#チップに搭載されている遺伝子のGene symbolsをgenenamesに格納 tmpAD <- AD[genenames] out <- apply(as.matrix(tmpAD), 1, calc_color) tmp3 <- cbind(genenames, tmpAD) #genenamesの右側にAD統計量情報を追加してtmp3に格納 write.table(tmp3, out_f3, sep="\t", append=F, quote=F, row.names=F, col.names=F)#tmpの中身を指定したファイル名で保存 tmp4 <- cbind(genenames, out) #genenamesの右側に色の16進数値情報を追加してtmp4に格納 write.table(tmp4, out_f4, sep=" ", append=F, quote=F, row.names=F, col.names=F)#tmpの中身を指定したファイル名で保存
2. Color Objects in KEGG Pathwaysのページを開き、以下を実行
- 「Search against:」のところを自分がマップしたい生物種(この場合は「Homo Sapiens (Human)」)を選択
- 「Alternatively, enter the file name containing the data:」のところの
”参照”ボタンをクリックして、KEGG Pathway用出力ファイル(out_f4で指定したファイル名:この場合はhoge_kegg.txt)
を読み込ませ、Execボタンを押す - ”Pathway Search Result”のページに切り替わるので、
paramで指定した解析したいパスウェイID(候補リストのトップのほうに位置している場合がほとんど:この場合HSA04612)のものをクリック
解析 | 機能解析 | PAGE(Z-score)法(Kim_2005;統計量の変換なし)を用いてGene Ontology解析
デフォルトのPAGE法は遺伝子のランキングにAD法を採用していましたが、Z-score変換するやり方(参考文献3)もあります。参考文献3ではlog10変換したものを取り扱っているので、(a)ではunlogged data(sample17_unlog.txt)を読み込んでlog10変換してますが、log2変換後のデータ(sample17.txt)を取り扱うのが一般的だと思うので、(b)ではlog2変換後のデータを読み込んでそのまま解析しています。
解析例で示す8 samples×14026 genesからなる遺伝子発現行列データ(sample17_unlog.txt or sample17.txt)は、最初の4サンプルがG1群、残りの4サンプルがG2群です。
- Molecular Signatures Database (MSigDB)の
「Registration」のページで登録し、遺伝子セットをダウンロード可能な状態にする。 - Molecular Signatures Database (MSigDB)の
「Download gene sets」の"Download"のところをクリックし、Loginページで登録したe-mail addressを入力。 - これでMSigDBのダウンロードページに行けるので、
とりあえず「c5: gene ontology gene sets」の「GO biological process gene sets file」を解析すべく、
c5.bp.v4.0.symbols.gmtファイルを(data_GSE7623_unlog_nr.txtをダウンロードしたディレクトリと同じところに)ダウンロードする。 - Rを立ち上げ、読み込む二つのファイルを置いているディレクトリに移動し、以下をコピペ
(a) log変換されていないデータ(sample17_unlog.txt)を読み込んでlog10変換して解析する場合:
in_f1 <- "sample17_unlog.txt" #入力ファイル名(発現データファイル)を指定してin_f1に格納 in_f2 <- "c5.bp.v4.0.symbols.gmt" #入力ファイル名(遺伝子セットファイル)を指定してin_f2に格納 out_f <- "hoge.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 4 #G1群のサンプル数を指定 param_G2 <- 4 #G2群のサンプル数を指定 #必要なパッケージをロード library(PGSEA) #PGSEAパッケージ(ライブラリ)の読み込み #入力ファイルの読み込みとラベル情報の作成 gmt <- readGmt(in_f2) #in_f2で指定したファイルの読み込み(不完全な最終行が見つかりました、となっても気にしない) data <- read.table(in_f1, header=TRUE, row.names=1, sep="\t", quote="")#in_f1で指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 colnames(data) #確認してるだけです #列(サンプル)ごとにZスコアを算出 data_log10 <- log10(data) #log10変換した結果をdata_log10に格納 zscore <- scale(data_log10) #Z-score化した結果をzscoreに格納 apply(zscore, 2, sd) #Z-score化した結果の各列の標準偏差がちゃんと1になっているか確認している apply(zscore, 2, mean) #Z-score化した結果の各列の平均がちゃんと0になっているか確認している #比較する2群間のZ ratioを算出 mean_zscore_A <- apply(zscore[,data.cl == 1], 1, mean)#G1群の行(遺伝子)ごとのzscoreの平均値を計算した結果をmean_zscore_Aに格納 mean_zscore_B <- apply(zscore[,data.cl == 2], 1, mean)#G2群の行(遺伝子)ごとのzscoreの平均値を計算した結果をmean_zscore_Bに格納 zratio <- (mean_zscore_B - mean_zscore_A)/sd(mean_zscore_B - mean_zscore_A)#Z ratioを計算した結果をzratioに格納 #Zスコアを算出する関数calc_zを作成 calc_z <- function(x, AD1, mean_set1, sd_set1){#Zスコアを算出する関数calc_zを作成 hoge <- (mean_set1 - mean(AD1[intersect(names(AD1), x)], na.rm=TRUE))*sqrt(length(intersect(names(AD1), x)))/sd_set1#Zスコアを算出する関数calc_zを作成 return(hoge) #Zスコアを算出する関数calc_zを作成 } #Zスコアを算出する関数calc_zを作成 #PAGE解析のメイン部分 AD <- zratio #この行以下の記述を他のPAGE法のものと統一すべくzratioをADとして取り扱う names(AD) <- toupper(names(AD)) #.gmtファイルは大文字の遺伝子名なのでnames(AD)でみられる遺伝子名も大文字に変換する mean_set <- mean(AD) #全遺伝子の倍率変化の平均を計算し、mean_setに格納 sd_set <- sd(AD) #全遺伝子の倍率変化の標準偏差を計算し、sd_setに格納 z_page <- NULL #おまじない for(i in 1:length(gmt)){ #length(gmt)回だけループを回す z_page <- c(z_page, calc_z(gmt[[i]]@ids, AD, mean_set, sd_set))#gmt[[i]]@idsで表されるi番目の遺伝子セットの遺伝子群のZスコアを計算し、z_pageに格納 } #length(gmt)回だけループを回す p_page <- (1 - pnorm(abs(z_page)))*2 #Zスコアに対応するp値を計算し、p_pageに格納 #結果をまとめてファイルに保存 out <- NULL #おまじない for(i in 1:length(gmt)){ #length(gmt)回だけループを回す Geneset_name <- gmt[[i]]@reference #遺伝子セット名をGeneset_nameに格納 GO_ID <- substring(gmt[[i]]@desc, 32, 41)#遺伝子セット名に対応するGene Ontology IDをGO_IDに格納 Member_num <- length(gmt[[i]]@ids) #各遺伝子セットを構成する遺伝子数をMember_numに格納 Member_num_thischip <- length(intersect(names(AD), gmt[[i]]@ids))#各遺伝子セットを構成する"このチップに搭載されている"遺伝子数をMember_num_thischipに格納 out <- rbind(out, c(Geneset_name, GO_ID, Member_num, Member_num_thischip))#Geneset_name, Member_num, Member_num_thischipの情報をoutに格納 } #length(gmt)回だけループを回す colnames(out) <- c("Geneset_name", "GO_ID", "Member_num", "Member_num_thischip")#列名を付与 #ファイルに保存 tmp <- cbind(out, z_page, p_page) #outの右側にPAGE解析結果のZスコアとp値を追加してtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存 #以下は(こんなこともできますという)おまけ #p値の低い順にソートした結果を得たい場合: out_f2 <- "hoge2.txt" #出力ファイル名を指定してout_f2に格納 tmp2 <- tmp[order(p_page),] #p値(p_page)でソートした結果をtmp2に格納 write.table(tmp2, out_f2, sep="\t", append=F, quote=F, row.names=F)#tmp2の中身を指定したファイル名で保存
(b) log2変換されたデータ(sample17.txt)を読み込んでそのまま解析する場合:
in_f1 <- "sample17.txt" #入力ファイル名(発現データファイル)を指定してin_f1に格納 in_f2 <- "c5.bp.v4.0.symbols.gmt" #入力ファイル名(遺伝子セットファイル)を指定してin_f2に格納 out_f <- "hoge.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 4 #G1群のサンプル数を指定 param_G2 <- 4 #G2群のサンプル数を指定 #必要なパッケージをロード library(PGSEA) #PGSEAパッケージ(ライブラリ)の読み込み #入力ファイルの読み込みとラベル情報の作成 gmt <- readGmt(in_f2) #in_f2で指定したファイルの読み込み(不完全な最終行が見つかりました、となっても気にしない) data <- read.table(in_f1, header=TRUE, row.names=1, sep="\t", quote="")#in_f1で指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 colnames(data) #確認してるだけです #列(サンプル)ごとにZスコアを算出 zscore <- scale(data) #Z-score化した結果をzscoreに格納 apply(zscore, 2, sd) #Z-score化した結果の各列の標準偏差がちゃんと1になっているか確認している apply(zscore, 2, mean) #Z-score化した結果の各列の平均がちゃんと0になっているか確認している #比較する2群間のZ ratioを算出 mean_zscore_A <- apply(zscore[,data.cl == 1], 1, mean)#G1群の行(遺伝子)ごとのzscoreの平均値を計算した結果をmean_zscore_Aに格納 mean_zscore_B <- apply(zscore[,data.cl == 2], 1, mean)#G2群の行(遺伝子)ごとのzscoreの平均値を計算した結果をmean_zscore_Bに格納 zratio <- (mean_zscore_B - mean_zscore_A)/sd(mean_zscore_B - mean_zscore_A)#Z ratioを計算した結果をzratioに格納 #Zスコアを算出する関数calc_zを作成 calc_z <- function(x, AD1, mean_set1, sd_set1){#Zスコアを算出する関数calc_zを作成 hoge <- (mean_set1 - mean(AD1[intersect(names(AD1), x)], na.rm=TRUE))*sqrt(length(intersect(names(AD1), x)))/sd_set1#Zスコアを算出する関数calc_zを作成 return(hoge) #Zスコアを算出する関数calc_zを作成 } #Zスコアを算出する関数calc_zを作成 #PAGE解析のメイン部分 AD <- zratio #この行以下の記述を他のPAGE法のものと統一すべくzratioをADとして取り扱う names(AD) <- toupper(names(AD)) #.gmtファイルは大文字の遺伝子名なのでnames(AD)でみられる遺伝子名も大文字に変換する mean_set <- mean(AD) #全遺伝子の倍率変化の平均を計算し、mean_setに格納 sd_set <- sd(AD) #全遺伝子の倍率変化の標準偏差を計算し、sd_setに格納 z_page <- NULL #おまじない for(i in 1:length(gmt)){ #length(gmt)回だけループを回す z_page <- c(z_page, calc_z(gmt[[i]]@ids, AD, mean_set, sd_set))#gmt[[i]]@idsで表されるi番目の遺伝子セットの遺伝子群のZスコアを計算し、z_pageに格納 } #length(gmt)回だけループを回す p_page <- (1 - pnorm(abs(z_page)))*2 #Zスコアに対応するp値を計算し、p_pageに格納 #結果をまとめてファイルに保存 out <- NULL #おまじない for(i in 1:length(gmt)){ #length(gmt)回だけループを回す Geneset_name <- gmt[[i]]@reference #遺伝子セット名をGeneset_nameに格納 GO_ID <- substring(gmt[[i]]@desc, 32, 41)#遺伝子セット名に対応するGene Ontology IDをGO_IDに格納 Member_num <- length(gmt[[i]]@ids) #各遺伝子セットを構成する遺伝子数をMember_numに格納 Member_num_thischip <- length(intersect(names(AD), gmt[[i]]@ids))#各遺伝子セットを構成する"このチップに搭載されている"遺伝子数をMember_num_thischipに格納 out <- rbind(out, c(Geneset_name, GO_ID, Member_num, Member_num_thischip))#Geneset_name, Member_num, Member_num_thischipの情報をoutに格納 } #length(gmt)回だけループを回す colnames(out) <- c("Geneset_name", "GO_ID", "Member_num", "Member_num_thischip")#列名を付与 #ファイルに保存 tmp <- cbind(out, z_page, p_page) #outの右側にPAGE解析結果のZスコアとp値を追加してtmpに格納 write.table(tmp, out_f, sep="\t", append=F, quote=F, row.names=F)#tmpの中身を指定したファイル名で保存 #以下は(こんなこともできますという)おまけ #p値の低い順にソートした結果を得たい場合: out_f2 <- "hoge2.txt" #出力ファイル名を指定してout_f2に格納 tmp2 <- tmp[order(p_page),] #p値(p_page)でソートした結果をtmp2に格納 write.table(tmp2, out_f2, sep="\t", append=F, quote=F, row.names=F)#tmp2の中身を指定したファイル名で保存
解析 | 機能解析 | Parametric Gene Set Enrichment Analysis (PGSEA) (Kim_2005)
解析 | 機能解析(GSEA周辺)についてでも書きましたが、原著論文(Kim and Volsky, BMC Bioinformatics, 2005)と似て非なるものです...。
library(PGSEA) #パッケージの読み込み library(GSEABase) #パッケージの読み込み library(org.Hs.eg.db) #パッケージの読み込み
解析 | 分類 | k-Nearest Neighbor (k-NN)
k-Nearest Neighbor (k-NN) 法を用いて分類します。ここではk=3とする場合について示します(距離の計算は"ユークリッド距離(Euclidean distance)"だけでしか行えないようです)。 分類に用いる遺伝子セットの選択(Feature selection)を不等分散性を仮定したt統計量(Welch t statistic)で行う場合の例を紹介します。 また、ここでは分類精度を交差検証法の一種であるLeave-one-out cross validation(LOOCV)を用いて行っています。分類精度は用いる遺伝子数によって変わりますので、 ここでは上位2, 3, ..., 15個を分類に用いた場合の結果を出力するようにしています。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動。
1. サンプルデータのdata_Singh_RMA_3274.txt(log2-transformed data)の場合:
RMA-preprocessed data (G1群:50 samples vs. G2群:52 samples)です。
Feature selectionを不等分散性を仮定したt統計量(Welch t statistic)で行うやり方です。
in_f <- "data_Singh_RMA_3274.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge1.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 50 #G1群のサンプル数を指定 param_G2 <- 52 #G2群のサンプル数を指定 #必要なパッケージをロード library(class) #パッケージの読み込み #ラベルが「1の群」と「2の群」間で不等分散性を仮定(var.equal=F)してt.testを行い、t統計量の値を返す関数Welch_tstatを作成。 Welch_tstat <- function(x, cl){ x.class1 <- x[(cl == 1)] #ラベルが1のものをx.class1に格納 x.class2 <- x[(cl == 2)] #ラベルが2のものをx.class2に格納 if((sd(x.class1)+sd(x.class2)) == 0){#両方の群の標準偏差が共に0の場合はt統計量を計算できない(無限大になる)ので、この場合の統計量を0にする statistic <- 0 return(statistic) } else{ hoge <- t.test(x.class1, x.class2, var.equal=F) return(hoge$statistic) } } #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#入力ファイルを読み込んでdataに格納 data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #本番 rank.matrix <- rownames(data) #おまじない(出力ファイルの一列目にrownames(data)情報(つまり遺伝子名に関する情報)を付加するため for (i in 1:length(data.cl)){ #LOOCVなので、length(data.cl)回数分だけループを回す data.tmp <- data[,-i] #i番目の列データを削除した結果をdata.tmpに格納 data.cl.tmp <- data.cl[-i] #i番目の列データに対応するラベル情報を削除した結果をdata.cl.tmpに格納 tmpall <- apply(data.tmp, 1, Welch_tstat, data.cl.tmp)#i番目の列データがないサブセットに対してWelch t-statisticを計算し、結果をtmpallに格納 rank.matrix <- cbind(rank.matrix, rank(-abs(tmpall)))#i番目の列データがないサブセットに対してWelch t-statisticを計算して得られたランキング結果をrank.matrixの右側の列に追加 } write.table(rank.matrix, "hoge_loocv.txt", sep = "\t", append=F, quote=F, row.names=F)#LOOCV用の「leave-one-outで得られたi番目の列(サンプル)データを削除した場合のランキング結果」を"hoge_loocv.txt"に出力 result <- c("No. of genes", "Accuracy", "MCC")#おまじない(出力ファイルの一行目に左記情報を付加するため) data.tmp <- read.table("hoge_loocv.txt", header=TRUE, row.names=1, sep="\t", quote="")#上記出力ファイルの読み込み for(g_num in 2:15){ #ランキング上位2, 3, ..., 15個を分類に用いた場合の精度を調べるためのループ pred.vector <- NULL #おまじない for(j in 1:ncol(data.tmp)){ #LOOCV用のループ(サンプル数分だけループが回る) data.rank <- data.tmp[,j] #j番目のカラム中のランキング情報をdata.rankに格納 data.s <- data[order(data.rank),]#もとの遺伝子発現行列data中の並びをdata.rankの並びでソートし直し、その結果をdata.sに格納 data.sub.train <- data.s[1:g_num,-j]#data.sに対して上位g_num個分までのj列目を除く遺伝子発現データをdata.sub.trainに格納(トレーニングデータ) data.sub.test <- data.s[1:g_num,j]#data.sに対して上位g_num個分までのj列目の遺伝子発現データをdata.sub.testに格納(テストデータ) data.cl.train <- data.cl[-j] #data.cl中のj番目を除くラベルデータをdata.cl.trainに格納(トレーニングデータ) data.cl.test <- data.cl[j] #data.cl中のj番目のラベルデータをdata.cl.testに格納(テストデータ) predicted <- knn(t(data.sub.train), t(data.sub.test), k=3, factor(data.cl.train))#k-Nearest Neighbor(k=3)の実行 pred.vector <- c(pred.vector, as.vector(predicted))#j番目のテストデータの結果をどんどんpred.vectorに格納していく } CrossTable <- table(true = data.cl, pred = pred.vector)#当たり外れのクロス集計表を作成 TN <- CrossTable[1,1] #True Negative(実際のラベルが0のものを正しく0と予測できた数)をTNに格納 FP <- CrossTable[1,2] #False Positive(実際のラベルが0のものを誤って1と予測してしまった数)をFPに格納 FN <- CrossTable[2,1] #False Positive(実際のラベルが1のものを誤って0と予測してしまった数)をFNに格納 TP <- CrossTable[2,2] #True Positive(実際のラベルが1のものを正しく1と予測できた数)をTPに格納 accuracy = (TP+TN)/(TP+FP+FN+TN) #Accuracyの計算 MCC = (TP*TN-FP*FN)/sqrt((TP+FN)*(TN+FP)*(TP+FP)*(TN+FN))#Matthews correlation coefficient(マシュー相関係数)の計算 result <- rbind(result, c(g_num, accuracy, MCC))#g_num, accuracy, MCCの値をベクトル化して、ベクトルresultの下の行に追加 } write.table(result, out_f, sep = "\t", append=F, quote=F, row.names=F)#結果をout_fで指定したファイル名で出力
解析 | 分類 | Self-Organizing Maps (SOM)
Self-Organizing Maps (SOM) 法を用いて分類します。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動。
library(class) #パッケージの読み込み
解析 | 分類 | Support Vector Machine (SVM)
Support Vector Machine (SVM) 法を用いて分類します。分類に用いる遺伝子セットの選択(Feature selection)をRank product (Breitling et al., FEBS Lett., 2004)) で行う場合とempirical Bayes statistic (経験ベイズ; Smyth GK, Stat. Appl, Genet. Mol. Biol., 2004))で行う場合の二通りの例を紹介します。 また、ここでは分類精度を交差検証法の一種であるLeave-one-out cross validation(LOOCV)を用いて行っています。
分類精度は用いる遺伝子数によって変わりますので、ここでは上位2, 3, ..., 100個を分類に用いた場合の結果を出力するようにしています。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動。
1. サンプルデータのdata_Singh_RMA_3274.txt(log2-transformed data)の場合:
RMA-preprocessed data (G1群:50 samples vs. G2群:52 samples)です。
Feature selectionをRank product (Breitling et al., FEBS Lett., 2004))で行うやり方です。
in_f <- "data_Singh_RMA_3274.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge1.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 50 #G1群のサンプル数を指定 param_G2 <- 52 #G2群のサンプル数を指定 #必要なパッケージをロード library(e1071) #パッケージの読み込み library(RankProd) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#入力ファイルを読み込んでdataに格納 data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #本番 rank.matrix <- rownames(data) #おまじない(出力ファイルの一列目にrownames(data)情報(つまり遺伝子名に関する情報)を付加するため for (i in 1:length(data.cl)){ #LOOCVなので、length(data.cl)回数分だけループを回す data.tmp <- data[,-i] #i番目の列データを削除した結果をdata.tmpに格納 data.cl.tmp <- data.cl[-i] #i番目の列データに対応するラベル情報を削除した結果をdata.cl.tmpに格納 tmpall <- RP(data.tmp, data.cl.tmp, num.perm=1, logged=TRUE, na.rm = FALSE, plot = FALSE, rand = 123)#i番目の列データがないサブセットに対してRank productを実行し、結果をtmpallに格納 tmprankall <- rank(apply(tmpall$RPs, 1, min))#Rank productは(1) Normal > Tumorの統計量RPと(2) Normal < Tumorの統計量RPの2つを別々の列として結果を返すため、各遺伝子(各行)に対して2つの値の低いほうの値をその遺伝子の統計量とした結果をtmprankallとして返す rank.matrix <- cbind(rank.matrix, tmprankall)#i番目の列データがないサブセットに対してRank productを実行して得られたランキング結果をrank.matrixの右側の列に追加 } write.table(rank.matrix, "hoge_loocv.txt", sep = "\t", append=F, quote=F, row.names=F)#LOOCV用の「leave-one-outで得られたi番目の列(サンプル)データを削除した場合のランキング結果」を"hoge_loocv.txt"に出力 result <- c("No. of genes", "Accuracy", "MCC")#おまじない(出力ファイルの一行目に左記情報を付加するため) data.tmp <- read.table("hoge_loocv.txt", header=TRUE, row.names=1, sep="\t", quote="")#上記出力ファイルの読み込み for(g_num in 2:100){ #ランキング上位2, 3, ..., 100個を分類に用いた場合の精度を調べるためのループ pred.vector <- NULL #おまじない for(j in 1:ncol(data.tmp)){ #LOOCV用のループ(サンプル数分だけループが回る) data.rank <- data.tmp[,j] #j番目のカラム中のランキング情報をdata.rankに格納 data.s <- data[order(data.rank),]#もとの遺伝子発現行列data中の並びをdata.rankの並びでソートし直し、その結果をdata.sに格納 data.sub.train <- data.s[1:g_num,-j]#data.sに対して上位g_num個分までのj列目を除く遺伝子発現データをdata.sub.trainに格納(トレーニングデータ) data.sub.test <- data.s[1:g_num,j]#data.sに対して上位g_num個分までのj列目の遺伝子発現データをdata.sub.testに格納(テストデータ) data.cl.train <- data.cl[-j] #data.cl中のj番目を除くラベルデータをdata.cl.trainに格納(トレーニングデータ) data.cl.test <- data.cl[j] #data.cl中のj番目のラベルデータをdata.cl.testに格納(テストデータ) svm.model <- svm(x=t(data.sub.train), y=factor(data.cl.train), scale=T, type="C-classification", kernel="linear")#トレーニングデータでsvmの実行 predicted <- predict(svm.model, t(data.sub.test))#得られたsvm.modelを用いてj番目のテストデータの予測を行い、結果をpredictedに格納 pred.vector <- c(pred.vector, as.vector(predicted))#j番目のテストデータの結果をどんどんpred.vectorに格納していく } CrossTable <- table(true = data.cl, pred = pred.vector)#当たり外れのクロス集計表を作成 TN <- CrossTable[1,1] #True Negative(実際のラベルが0のものを正しく0と予測できた数)をTNに格納 FP <- CrossTable[1,2] #False Positive(実際のラベルが0のものを誤って1と予測してしまった数)をFPに格納 FN <- CrossTable[2,1] #False Positive(実際のラベルが1のものを誤って0と予測してしまった数)をFNに格納 TP <- CrossTable[2,2] #True Positive(実際のラベルが1のものを正しく1と予測できた数)をTPに格納 accuracy = (TP+TN)/(TP+FP+FN+TN) #Accuracyの計算 MCC = (TP*TN-FP*FN)/sqrt((TP+FN)*(TN+FP)*(TP+FP)*(TN+FN))#Matthews correlation coefficient(マシュー相関係数)の計算 result <- rbind(result, c(g_num, accuracy, MCC))#g_num, accuracy, MCCの値をベクトル化して、ベクトルresultの下の行に追加 } write.table(result, out_f, sep = "\t", append=F, quote=F, row.names=F)#結果をout_fで指定したファイル名で出力
2. Feature selectionをempirical Bayes statistic (経験ベイズ; Smyth GK, Stat. Appl, Genet. Mol. Biol., 2004))で行う場合:
in_f <- "data_Singh_RMA_3274.txt" #入力ファイル名を指定してin_fに格納 out_f <- "result_loocv.txt" #出力ファイル名を指定してout_fに格納 param_G1 <- 50 #G1群のサンプル数を指定 param_G2 <- 52 #G2群のサンプル数を指定 #必要なパッケージをロード library(e1071) #パッケージの読み込み #入力ファイルの読み込みとラベル情報の作成 data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 #本番 rank.matrix <- rownames(data) #おまじない(出力ファイルの一列目にrownames(data)情報(つまり遺伝子名に関する情報)を付加するため for (i in 1:length(data.cl)){ #LOOCVなので、length(data.cl)回数分だけループを回す data.tmp <- data[,-i] #i番目の列データを削除した結果をdata.tmpに格納 data.cl.tmp <- data.cl[-i] #i番目の列データに対応するラベル情報を削除した結果をdata.cl.tmpに格納 design <- model.matrix(~data.cl.tmp)#おまじない fit <- lmFit(data.tmp, design) #おまじない eb2 <- eBayes(fit) #おまじない tmp.out <- topTable(eb2, coef=2, number=(length(row.names(data))),adjust="fdr")#おまじない tmpall <- tmp.out[order(tmp.out[,1]),]#おまじない rank.matrix <- cbind(rank.matrix, rank(-abs(tmpall$t)))#i番目の列データがないサブセットに対してEmpirical bayesを実行して得られたランキング結果をrank.matrixの右側の列に追加 } write.table(rank.matrix, "hoge_loocv.txt", sep = "\t", append=F, quote=F, row.names=F)#LOOCV用の「leave-one-outで得られたi番目の列(サンプル)データを削除した場合のランキング結果」をhoge_loocv.txtに出力 result <- c("No. of genes", "Accuracy", "MCC")#おまじない(出力ファイルの一行目に左記情報を付加するため) data.tmp <- read.table("hoge_loocv.txt", header=TRUE, row.names=1, sep="\t", quote="")#上記出力ファイルの読み込み for(g_num in 2:100){ #ランキング上位2, 3, ..., 100個を分類に用いた場合の精度を調べるためのループ pred.vector <- NULL #おまじない for(j in 1:ncol(data.tmp)){ #LOOCV用のループ(サンプル数分だけループが回る) data.rank <- data.tmp[,j] #j番目のカラム中のランキング情報をdata.rankに格納 data.s <- data[order(data.rank),]#もとの遺伝子発現行列data中の並びをdata.rankの並びでソートし直し、その結果をdata.sに格納 data.sub.train <- data.s[1:g_num,-j]#data.sに対して上位g_num個分までのj列目を除く遺伝子発現データをdata.sub.trainに格納(トレーニングデータ) data.sub.test <- data.s[1:g_num,j]#data.sに対して上位g_num個分までのj列目の遺伝子発現データをdata.sub.testに格納(テストデータ) data.cl.train <- data.cl[-j] #data.cl中のj番目を除くラベルデータをdata.cl.trainに格納(トレーニングデータ) data.cl.test <- data.cl[j] #data.cl中のj番目のラベルデータをdata.cl.testに格納(テストデータ) svm.model <- svm(x=t(data.sub.train), y=factor(data.cl.train), scale=T, type="C-classification", kernel="linear")#トレーニングデータでsvmの実行 predicted <- predict(svm.model, t(data.sub.test))#得られたsvm.modelを用いてj番目のテストデータの予測を行い、結果をpredictedに格納 pred.vector <- c(pred.vector, as.vector(predicted))#j番目のテストデータの結果をどんどんpred.vectorに格納していく } CrossTable <- table(true = data.cl, pred = pred.vector)#当たり外れのクロス集計表を作成 TN <- CrossTable[1,1] #True Negative(実際のラベルが0のものを正しく0と予測できた数)をTNに格納 FP <- CrossTable[1,2] #False Positive(実際のラベルが0のものを誤って1と予測してしまった数)をFPに格納 FN <- CrossTable[2,1] #False Positive(実際のラベルが1のものを誤って0と予測してしまった数)をFNに格納 TP <- CrossTable[2,2] #True Positive(実際のラベルが1のものを正しく1と予測できた数)をTPに格納 accuracy = (TP+TN)/(TP+FP+FN+TN) #Accuracyの計算 MCC = (TP*TN-FP*FN)/sqrt((TP+FN)*(TN+FP)*(TP+FP)*(TN+FN)) #Matthews correlation coefficient(マシュー相関係数)の計算 result <- rbind(result, c(g_num, accuracy, MCC))#g_num, accuracy, MCCの値をベクトル化して、ベクトルresultの下の行に追加 } write.table(result, out_f, sep = "\t", append=F, quote=F, row.names=F)#結果をout_fで指定したファイル名で出力
解析 | 分類 | Naive Bayesian (NB)
Naive Bayesian (NB) 法を用いて分類します。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動。
library(e1071) #パッケージの読み込み
解析 | アレイCGH(DNAコピー数)解析 | について
アレイCGH(Comparative Genomic Hybridization)法は、もともとは腫瘍組織で染色体に異常が生じている領域を正常組織との比較により同定することを目的とした解析技術です。二色法のマイクロアレイと本質的に同じ。
目的がDNAコピー数が変化している領域を同定(アレイCGH;この意味において、”DNAコピー数解析”などとも呼ばれます)するか、発現変動遺伝子の同定(従来型の二色法マイクロアレイの利用)などかという程度の違いです。
昔はBACクローンなどがアレイに搭載されていて解像度がそれほど高くありませんでしたが、最近ではタイリングアレイのような感じでかなり高い解像度のデータが得られるようになっているようです。したがって得られるデータのイメージ図は、「横軸:ゲノム上の位置、縦軸:比較二つのサンプルのlog比」です。
「比較二つのサンプルのlog比のデータ」を入力として与えて、「”連続してlog比の絶対値が高い領域”のリストやそれの図」を出力として返してくれます。
2013年6月に調査した結果をリストアップします。
- GLAD:Hupe et al., Bioinformatics, 2004
- CBS (DNAcopyパッケージ):Olshen et al., Biostatistics, 2004
- faster CBS (DNAcopyパッケージ):Venkatraman and Olshen, Bioinformatics, 2007
- ADaCGH(Rだが、なくなっている):Diaz-Uriarte and Rueda, PLoS One, 2007
- DP-EM:Picard et al., Biometrics, 2007
- :Staaf et al., Genome Biol., 2008
- Ultrasome:Nilsson et al., Bioinformatics, 2009
- CGHnormaliter:van Houte et al., Bioinformatics, 2010
- MDLS:Wang et al., J Bioinform Comput Biol., 2011
- parsimonious higher-order HMMs:Seifert et al., PLoS Comput Biol., 2012
- GFL:Zhang et al., BMC Bioinformatics, 2012
- :Scharpf et al., BMC Bioinformatics, 2012
- CnaStruct:Mosen-Ansorena and Aransay, BMC Bioinformatics, 2013
解析 | アレイCGH(DNAコピー数)解析 | GLAD (Hupe_2004)
GLADパッケージを用いて解析を行う。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動。
library(GLAD) #パッケージの読み込み
解析 | アレイCGH(DNAコピー数)解析 | DNAcopy (Olshen_2004)
DNAcopyパッケージを用いて解析を行う。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動。
library(DNAcopy) #パッケージの読み込み
作図 | M-A plot
サンプルデータの31,099 probesets×24 samplesのデータを読み込んでM-Aプロットを作成します。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動し以下をコピペ。
1. 31,099 probesets×24 samplesのMAS5-preprocessedデータ(data_mas.txt)の場合:
(データを読み込んだ後に、最初の4列分(Brown adopise tissue)のみ抽出して2 fed samples vs. 2 fed samplesの2群間比較データとして取り扱っています)
in_f <- "data_mas.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge1.png" #出力ファイル名を指定してout_fに格納 param_G1 <- 2 #G1群(fed)のサンプル数を指定 param_G2 <- 2 #G2群(fasted)のサンプル数を指定 param_fig <- c(400, 380) #ファイル出力時の横幅と縦幅を指定(単位はピクセル) #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #前処理(対数変換後のデータなのでオリジナルスケールに変換したのち、最初の4列分のみ抽出) data <- 2^data #データ変換 data <- data[,1:4] #最初の8列分のデータのみ抽出している #前処理(M-A plotのための基礎情報取得) data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 G1 <- apply(as.matrix(data[,data.cl==1]), 1, mean)#遺伝子ごとにG1群の平均を計算した結果をG1に格納 G2 <- apply(as.matrix(data[,data.cl==2]), 1, mean)#遺伝子ごとにG2群の平均を計算した結果をG2に格納 M <- log2(G2) - log2(G1) #M-A plotのM(y軸の値)に相当するものをMに格納) A <- (log2(G1) + log2(G2))/2 #M-A plotのA(x軸の値)に相当するものをAに格納) #ファイルに保存(M-A plot) png(out_f, pointsize=13, width=param_fig[1], height=param_fig[2])#出力ファイルの各種パラメータを指定 plot(A, M, xlab="A = (log2(G2)+log2(G1))/2", ylab="M = log2(G2)-log2(G1)",#M-A plotを描画 ylim=c(-7, 7), xlim=c(0, 16), pch=20, cex=.1)#M-A plotを描画 grid(col="gray", lty="dotted") #指定したパラメータでグリッドを表示 median(M, na.rm=TRUE) #M値(=log2(G2/G1))の中央値(Inf and -Infを含む)を表示 abline(h=median(M, na.rm=TRUE), col="black")#M値(=log2(G2/G1))の中央値を指定した色で表示 #後処理(いろいろな条件を満たすものを描画している) obj <- (abs(M) >= 1) #「2倍以上発現変動している遺伝子」という条件を指定 points(A[obj], M[obj], col="magenta", cex=0.8, pch=6)#objがTRUEとなる要素のみ指定した色で描画 sum(obj, na.rm=TRUE) #objがTRUEとなる要素数を表示させている dev.off() #おまじない
2. 31,099 probesets×24 samplesのRMA-preprocessedデータ(data_rma_2.txt)の場合:
(データを読み込んだ後に、最初の4列分(Brown adopise tissue)のみ抽出して2 fed samples vs. 2 fed samplesの2群間比較データとして取り扱っています)
in_f <- "data_rma_2.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge2.png" #出力ファイル名を指定してout_fに格納 param_G1 <- 2 #G1群(fed)のサンプル数を指定 param_G2 <- 2 #G2群(fasted)のサンプル数を指定 param_fig <- c(400, 380) #ファイル出力時の横幅と縦幅を指定(単位はピクセル) #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み #前処理(対数変換後のデータなのでオリジナルスケールに変換したのち、最初の4列分のみ抽出) data <- 2^data #データ変換 data <- data[,1:4] #最初の8列分のデータのみ抽出している #前処理(M-A plotのための基礎情報取得) data.cl <- c(rep(1, param_G1), rep(2, param_G2))#G1群を1、G2群を2としたベクトルdata.clを作成 G1 <- apply(as.matrix(data[,data.cl==1]), 1, mean)#遺伝子ごとにG1群の平均を計算した結果をG1に格納 G2 <- apply(as.matrix(data[,data.cl==2]), 1, mean)#遺伝子ごとにG2群の平均を計算した結果をG2に格納 M <- log2(G2) - log2(G1) #M-A plotのM(y軸の値)に相当するものをMに格納) A <- (log2(G1) + log2(G2))/2 #M-A plotのA(x軸の値)に相当するものをAに格納) #ファイルに保存(M-A plot) png(out_f, pointsize=13, width=param_fig[1], height=param_fig[2])#出力ファイルの各種パラメータを指定 plot(A, M, xlab="A = (log2(G2)+log2(G1))/2", ylab="M = log2(G2)-log2(G1)",#M-A plotを描画 ylim=c(-7, 7), xlim=c(0, 16), pch=20, cex=.1)#M-A plotを描画 grid(col="gray", lty="dotted") #指定したパラメータでグリッドを表示 median(M, na.rm=TRUE) #M値(=log2(G2/G1))の中央値(Inf and -Infを含む)を表示 abline(h=median(M, na.rm=TRUE), col="black")#M値(=log2(G2/G1))の中央値を指定した色で表示 #後処理(いろいろな条件を満たすものを描画している) obj <- (abs(M) >= 1) #「2倍以上発現変動している遺伝子」という条件を指定 points(A[obj], M[obj], col="magenta", cex=0.8, pch=6)#objがTRUEとなる要素のみ指定した色で描画 sum(obj, na.rm=TRUE) #objがTRUEとなる要素数を表示させている dev.off() #おまじない
作図 | ヒートマップ | 1. 感覚をつかむ
論文中でよく見かけるヒートマップ(pseudo-color image)を作成してくれます(例えばKadota et al., Physiol. Genomics, 2003 の図2を作成してくれます)。 ここでは、サンプルデータ26の仮想データを用いて示します。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動。
1. サンプルデータ26の仮想データ(sample26.txt)の場合:
23遺伝子×6サンプルのデータです。基本形です。 R Console画面の後ろのほうに、R Graphics画面が起動して描画されます。 デフォルトだと、クラスタリングも実行されるようです。 高発現が白で低発現が赤で示されています。 行ごとにスケーリングされていることもわかります。 gene3からgene21までは行方向がすべて同じ値のため、うまくスケーリングできずに赤と白の中間色ではなく全部白になっているのか、 それとも計算できないので空白の意味で白になっているのかは定かではありません。
in_f <- "sample26.txt" #入力ファイル名を指定してin_fに格納 #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み dim(data) #オブジェクトdataの行数と列数を表示 #本番 heatmap(as.matrix(data)) #ヒートマップの作成
2. サンプルデータ26の仮想データ(sample26.txt)の場合:
得られた図をサイズを指定して (700×400ピクセル)、PNG形式ファイル(ファイル名はhoge2.png)で保存するやり方です。 縦幅で決まっているようなので、横幅を変えても空白エリアが増えるだけのようです。
in_f <- "sample26.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge2.png" #出力ファイル名を指定してout_fに格納 param_fig <- c(700, 400) #ファイル出力時の横幅と縦幅を指定(単位はピクセル) #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み dim(data) #オブジェクトdataの行数と列数を表示 #本番 png(out_f, pointsize=13, width=param_fig[1], height=param_fig[2])#出力ファイルの各種パラメータを指定 heatmap(as.matrix(data)) #ヒートマップの作成 dev.off() #おまじない
3. サンプルデータ26の仮想データ(sample26.txt)の場合:
列方向(サンプル)のクラスタリングをやらずに、 入力ファイル通りの列の並びで表示させるやり方です。
in_f <- "sample26.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge3.png" #出力ファイル名を指定してout_fに格納 param_fig <- c(700, 400) #ファイル出力時の横幅と縦幅を指定(単位はピクセル) #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み dim(data) #オブジェクトdataの行数と列数を表示 #本番 png(out_f, pointsize=13, width=param_fig[1], height=param_fig[2])#出力ファイルの各種パラメータを指定 heatmap(as.matrix(data), Colv=NA) #ヒートマップの作成 dev.off() #おまじない
4. サンプルデータ26の仮想データ(sample26.txt)の場合:
行と列両方のクラスタリングをやらずに、 入力ファイル通りの行と列の並びで表示させるやり方です。
in_f <- "sample26.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge4.png" #出力ファイル名を指定してout_fに格納 param_fig <- c(700, 400) #ファイル出力時の横幅と縦幅を指定(単位はピクセル) #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み dim(data) #オブジェクトdataの行数と列数を表示 #本番 png(out_f, pointsize=13, width=param_fig[1], height=param_fig[2])#出力ファイルの各種パラメータを指定 heatmap(as.matrix(data), Colv=NA, Rowv=NA)#ヒートマップの作成 dev.off() #おまじない
作図 | ヒートマップ | 2. 色を自在に変える(col)
ヒートマップ(pseudo-color image)の色を変えるやり方を示します。heat.colors, cm.colors, topo.colors, g2r.colors, rainbowなどが選べます。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動。
1. サンプルデータ26の仮想データ(sample26.txt)の場合:
23遺伝子×6サンプルのデータです。デフォルトの高発現(白色)から低発現(赤色)の色指定を明示させただけです。 heat.colors(256)は、「暖色256段階」の意味です。
in_f <- "sample26.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge1.png" #出力ファイル名を指定してout_fに格納 param_fig <- c(700, 400) #ファイル出力時の横幅と縦幅を指定(単位はピクセル) #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み dim(data) #オブジェクトdataの行数と列数を表示 #本番 png(out_f, pointsize=13, width=param_fig[1], height=param_fig[2])#出力ファイルの各種パラメータを指定 heatmap(as.matrix(data), Colv=NA, #ヒートマップの作成 Rowv=NA, col=heat.colors(256)) #ヒートマップの作成 dev.off() #おまじない
2. サンプルデータ26の仮想データ(sample26.txt)の場合:
heat.colors(3)として、「暖色3段階」にしています。 gene1, 2, 22, 23で表示されている3色(黄色、オレンジ、赤)が3段階に相当すると思います。 gene3からgene21が白色で見えているのは、白ではなく空白という意味なのだろうと推測しています。
in_f <- "sample26.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge2.png" #出力ファイル名を指定してout_fに格納 param_fig <- c(700, 400) #ファイル出力時の横幅と縦幅を指定(単位はピクセル) #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み dim(data) #オブジェクトdataの行数と列数を表示 #本番 png(out_f, pointsize=13, width=param_fig[1], height=param_fig[2])#出力ファイルの各種パラメータを指定 heatmap(as.matrix(data), Colv=NA, #ヒートマップの作成 Rowv=NA, col=heat.colors(3)) #ヒートマップの作成 dev.off() #おまじない
3. サンプルデータ26の仮想データ(sample26.txt)の場合:
寒色の高発現(ピンク色)から低発現(水色)の色指定のやり方です。 cm.colors(3)として、「寒色3段階」にするやりかたです。 高発現(ピンク色)、中発現(白色)、低発現(水色)の三段階になるようです。
in_f <- "sample26.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge3.png" #出力ファイル名を指定してout_fに格納 param_fig <- c(700, 400) #ファイル出力時の横幅と縦幅を指定(単位はピクセル) #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み dim(data) #オブジェクトdataの行数と列数を表示 #本番 png(out_f, pointsize=13, width=param_fig[1], height=param_fig[2])#出力ファイルの各種パラメータを指定 heatmap(as.matrix(data), Colv=NA, #ヒートマップの作成 Rowv=NA, col=cm.colors(3)) #ヒートマップの作成 dev.off() #おまじない
4. サンプルデータ26の仮想データ(sample26.txt)の場合:
Heatplusパッケージで提供されている g2r.colors関数を利用して、「緑から赤への256段階」にするやりかたです。 昔のマイクロアレイの図での色使いです。
in_f <- "sample26.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge4.png" #出力ファイル名を指定してout_fに格納 param_fig <- c(700, 400) #ファイル出力時の横幅と縦幅を指定(単位はピクセル) #必要なパッケージをロード library(Heatplus) #パッケージの読み込み #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み dim(data) #オブジェクトdataの行数と列数を表示 #本番 png(out_f, pointsize=13, width=param_fig[1], height=param_fig[2])#出力ファイルの各種パラメータを指定 heatmap(as.matrix(data), Colv=NA, #ヒートマップの作成 Rowv=NA, col=g2r.colors(256)) #ヒートマップの作成 dev.off() #おまじない
作図 | ヒートマップ | 3. データを変換してから表示(scale)
ヒートマップ(pseudo-color image)時にデータを変換する/しない周辺を解説します。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動。
1. サンプルデータ26の仮想データ(sample26.txt)の場合:
23遺伝子×6サンプルのデータです。デフォルトの。scale="row"を明示しただけです。 内部的には行ごとに、おそらくZ scaling (Z-score化)をしているのだろうと思います。 Zスコア化することで、任意のベクトルが与えられたときに平均が0、標準偏差が1になるような変換 (the rows are scaled to have mean zero and standard deviation one)を行うことになります。 例えば、Golub et al., Science, 1999の図3などです。
in_f <- "sample26.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge1.png" #出力ファイル名を指定してout_fに格納 param_fig <- c(700, 400) #ファイル出力時の横幅と縦幅を指定(単位はピクセル) #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み dim(data) #オブジェクトdataの行数と列数を表示 #本番 png(out_f, pointsize=13, width=param_fig[1], height=param_fig[2])#出力ファイルの各種パラメータを指定 heatmap(as.matrix(data), Colv=NA, #ヒートマップの作成 Rowv=NA, col=heat.colors(256), #ヒートマップの作成 scale="row") #ヒートマップの作成 dev.off() #おまじない
2. サンプルデータ26の仮想データ(sample26.txt)の場合:
scale="none"としてスケーリングをしないやり方です。 見栄えが違うことがわかります。色調は、heat.colors(256)です。 gene1の発現レベル18が最大で、-18が最小値ですが、これが白色と赤色で表示されているのがわかります。
in_f <- "sample26.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge2.png" #出力ファイル名を指定してout_fに格納 param_fig <- c(700, 400) #ファイル出力時の横幅と縦幅を指定(単位はピクセル) #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み dim(data) #オブジェクトdataの行数と列数を表示 #本番 png(out_f, pointsize=13, width=param_fig[1], height=param_fig[2])#出力ファイルの各種パラメータを指定 heatmap(as.matrix(data), Colv=NA, #ヒートマップの作成 Rowv=NA, col=heat.colors(256), #ヒートマップの作成 scale="none") #ヒートマップの作成 dev.off() #おまじない
3. サンプルデータ26の仮想データ(sample26.txt)の場合:
scale="none"としてスケーリングをしないやり方です。 Heatplusパッケージで提供されている g2r.colors関数を利用して、「緑から赤への256段階」にするやりかたです。 gene1の発現レベル18が最大で、-18が最小値ですが、これが赤色と緑色で表示されているのがわかります。
in_f <- "sample26.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge3.png" #出力ファイル名を指定してout_fに格納 param_fig <- c(700, 400) #ファイル出力時の横幅と縦幅を指定(単位はピクセル) #必要なパッケージをロード library(Heatplus) #パッケージの読み込み #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み dim(data) #オブジェクトdataの行数と列数を表示 #本番 png(out_f, pointsize=13, width=param_fig[1], height=param_fig[2])#出力ファイルの各種パラメータを指定 heatmap(as.matrix(data), Colv=NA, #ヒートマップの作成 Rowv=NA, col=g2r.colors(256), #ヒートマップの作成 scale="none") #ヒートマップの作成 dev.off() #おまじない
作図 | ヒートマップ | 4. 余白を変える(margins)
ヒートマップ(pseudo-color image)時に余白を変えるやり方を示します。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動。
1. サンプルデータ26の仮想データ(sample26.txt)の場合:
23遺伝子×6サンプルのデータです。デフォルトのmargins=c(5, 5)を明示しただけです。 スケーリングを行っていない(scale="none")ので、 最大値(白色)と最小値(赤色)を含むgene1が最大のコントラストとなっているのがわかります。
in_f <- "sample26.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge1.png" #出力ファイル名を指定してout_fに格納 param_fig <- c(700, 400) #ファイル出力時の横幅と縦幅を指定(単位はピクセル) #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み dim(data) #オブジェクトdataの行数と列数を表示 #本番 png(out_f, pointsize=13, width=param_fig[1], height=param_fig[2])#出力ファイルの各種パラメータを指定 heatmap(as.matrix(data), Colv=NA, #ヒートマップの作成 Rowv=NA, col=heat.colors(256), #ヒートマップの作成 scale="none", margins=c(5, 5)) #ヒートマップの作成 dev.off() #おまじない
2. サンプルデータ26の仮想データ(sample26.txt)の場合:
23遺伝子×6サンプルのデータです。margins=c(3, 5)として、列名のマージンを狭くするやり方です。
in_f <- "sample26.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge2.png" #出力ファイル名を指定してout_fに格納 param_fig <- c(700, 400) #ファイル出力時の横幅と縦幅を指定(単位はピクセル) #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み dim(data) #オブジェクトdataの行数と列数を表示 #本番 png(out_f, pointsize=13, width=param_fig[1], height=param_fig[2])#出力ファイルの各種パラメータを指定 heatmap(as.matrix(data), Colv=NA, #ヒートマップの作成 Rowv=NA, col=heat.colors(256), #ヒートマップの作成 scale="none", margins=c(3, 5)) #ヒートマップの作成 dev.off() #おまじない
作図 | ヒートマップ | 5. 大きさを変える(cex)
ヒートマップ(pseudo-color image)時に列や行名の大きさを変えるやり方を示します。
「ファイル」−「ディレクトリの変更」で解析したいファイルを置いてあるディレクトリに移動。
1. サンプルデータ26の仮想データ(sample26.txt)の場合:
23遺伝子×6サンプルのデータです。cexCol=1.5として、列名を通常の1.5倍にしています。
in_f <- "sample26.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge1.png" #出力ファイル名を指定してout_fに格納 param_fig <- c(700, 400) #ファイル出力時の横幅と縦幅を指定(単位はピクセル) #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み dim(data) #オブジェクトdataの行数と列数を表示 #本番 png(out_f, pointsize=13, width=param_fig[1], height=param_fig[2])#出力ファイルの各種パラメータを指定 heatmap(as.matrix(data), Colv=NA, #ヒートマップの作成 Rowv=NA, col=heat.colors(256), #ヒートマップの作成 scale="none", margins=c(9, 5), #ヒートマップの作成 cexCol=1.5) #ヒートマップの作成 dev.off() #おまじない
2.GDS1096_best10_heart.txtの場合:
10遺伝子×36サンプルのデータです。cexCol=1.5として、列名を通常の1.5倍に、そして行名を通常の2.0倍にしています。
in_f <- "GDS1096_best10_heart.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge2.png" #出力ファイル名を指定してout_fに格納 param_fig <- c(700, 400) #ファイル出力時の横幅と縦幅を指定(単位はピクセル) #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み dim(data) #オブジェクトdataの行数と列数を表示 #本番 png(out_f, pointsize=13, width=param_fig[1], height=param_fig[2])#出力ファイルの各種パラメータを指定 heatmap(as.matrix(data), Colv=NA, #ヒートマップの作成 Rowv=NA, col=heat.colors(256), #ヒートマップの作成 scale="row", margins=c(9, 5), #ヒートマップの作成 cexCol=1.5, cexRow=2.0) #ヒートマップの作成 dev.off() #おまじない
3.GDS1096_best10_heart.txtの場合:
10遺伝子×36サンプルのデータです。図のサイズ列名、行名のサイズを変えています。
in_f <- "GDS1096_best10_heart.txt" #入力ファイル名を指定してin_fに格納 out_f <- "hoge3.png" #出力ファイル名を指定してout_fに格納 param_fig <- c(500, 600) #ファイル出力時の横幅と縦幅を指定(単位はピクセル) #入力ファイルの読み込み data <- read.table(in_f, header=TRUE, row.names=1, sep="\t", quote="")#in_fで指定したファイルの読み込み dim(data) #オブジェクトdataの行数と列数を表示 #本番 png(out_f, pointsize=13, width=param_fig[1], height=param_fig[2])#出力ファイルの各種パラメータを指定 heatmap(as.matrix(data), Colv=NA, #ヒートマップの作成 Rowv=NA, col=heat.colors(256), #ヒートマップの作成 scale="row", margins=c(9, 5), #ヒートマップの作成 cexCol=1.0, cexRow=1.5) #ヒートマップの作成 dev.off() #おまじない
作図 | ROC曲線(ROC curve)
ROC (Receiver Operating Characteristic)曲線は、横軸が偽陽性率(1-特異度;false positive rate)、縦軸が真陽性率(感度;true positive rate)としてプロットをしたものです。
例えばWAD (Kadota et al., AMB, 2008)は感度・特異度高く発現変動遺伝子をランキングできる方法だなどと書いていますが、
これはアレイ中の全遺伝子のWADでのランキング結果に対し”真の発現変動遺伝子”をマッピングしてROC曲線を描くと、このROC曲線の下部面積(Area Under the Curve; AUC)の値が大きい(最大値は1)ということを意味します。
もう少し具体的なイメージはこちらの32ページ目をご覧ください。
RでどうやってAUC値を得るかについてはこちらの33ページ目をご覧ください。
一応、以下にも例を示しておきます。
1. (param_Ngene)個の遺伝子をWADなどでランキングして、”真の発現変動遺伝子(DEG)”3個が1, 3, 4位だった。このAUC値:
param1 <- c(1,3,4) #真のDEGの順位情報を指定 param_Ngene <- 10 #全遺伝子数を指定 #必要なパッケージをロード library(ROC) #パッケージの読み込み #本番 DEG_posi <- rep(0, param_Ngene) #DEGの位置情報の初期値(0)を指定 DEG_posi <- replace(DEG_posi, param1, 1)#DEGに相当する位置を1に置換 out <- rocdemo.sca(truth=DEG_posi, data=-(1:param_Ngene), rule=dxrule.sca)#ROC情報をoutに格納 AUC(out) #AUC値を計算
2. このROC曲線の図:
param1 <- c(1,3,4) #真のDEGの順位情報を指定 param_Ngene <- 10 #全遺伝子数を指定 #必要なパッケージをロード library(ROC) #パッケージの読み込み #本番 DEG_posi <- rep(0, param_Ngene) #DEGの位置情報の初期値(0)を指定 DEG_posi <- replace(DEG_posi, param1, 1)#DEGに相当する位置を1に置換 out <- rocdemo.sca(truth=DEG_posi, data=-(1:param_Ngene), rule=dxrule.sca)#ROC情報をoutに格納 plot(out) #ROC曲線をプロット
3. このROC曲線をpng形式のファイルで図の大きさを指定して得たい場合:
out_f <- "hoge3.png" #出力ファイル名を指定してout_fに格納 param1 <- c(1,3,4) #真のDEGの順位情報を指定 param_Ngene <- 10 #全遺伝子数を指定 param_fig <- c(400, 400) #ファイル出力時の横幅と縦幅を指定(単位はピクセル) #必要なパッケージをロード library(ROC) #パッケージの読み込み #本番 DEG_posi <- rep(0, param_Ngene) #DEGの位置情報の初期値(0)を指定 DEG_posi <- replace(DEG_posi, param1, 1)#DEGに相当する位置を1に置換 out <- rocdemo.sca(truth=DEG_posi, data=-(1:param_Ngene), rule=dxrule.sca)#ROC情報をoutに格納 #ファイルに保存 png(out_f, pointsize=13, width=param_fig[1], height=param_fig[2])#出力ファイルの各種パラメータを指定 plot(out) #ROC曲線をプロット dev.off() #おまじない
4. このROC曲線をpng形式のファイルで図の大きさを指定して得たい場合(x,y軸の文字も指定):
out_f <- "hoge4.png" #出力ファイル名を指定してout_fに格納 param1 <- c(1,3,4) #真のDEGの順位情報を指定 param_Ngene <- 10 #全遺伝子数を指定 param_fig <- c(400, 400) #ファイル出力時の横幅と縦幅を指定(単位はピクセル) param6 <- "1 - specificity" #x軸のラベルを指定 param7 <- "sensitivity" #y軸のラベルを指定 #必要なパッケージをロード library(ROC) #パッケージの読み込み #本番 DEG_posi <- rep(0,param2) #DEGの位置情報の初期値(0)を指定 DEG_posi <- replace(DEG_posi, param1, 1)#DEGに相当する位置を1に置換 out <- rocdemo.sca(truth=DEG_posi, data=-(1:param_Ngene), rule=dxrule.sca)#ROC情報をoutに格納 #ファイルに保存 png(out_f, pointsize=13, width=param_fig[1], height=param_fig[2])#出力ファイルの各種パラメータを指定 plot(out, xlab=param6, ylab=param7) #ROC曲線をプロット dev.off() #おまじない
5. このROC曲線をpng形式のファイルで図の大きさを指定して得たい場合(x,y軸のラベルを描かないようにしたい):
out_f <- "hoge5.png" #出力ファイル名を指定してout_fに格納 param1 <- c(1,3,4) #真のDEGの順位情報を指定 param_Ngene <- 10 #全遺伝子数を指定 param_fig <- c(400, 400) #ファイル出力時の横幅と縦幅を指定(単位はピクセル) param6 <- "1 - specificity" #x軸のラベルを指定 param7 <- "sensitivity" #y軸のラベルを指定 #必要なパッケージをロード library(ROC) #パッケージの読み込み #本番 DEG_posi <- rep(0,param2) #DEGの位置情報の初期値(0)を指定 DEG_posi <- replace(DEG_posi, param1, 1)#DEGに相当する位置を1に置換 out <- rocdemo.sca(truth=DEG_posi, data=-(1:param_Ngene), rule=dxrule.sca)#ROC情報をoutに格納 #ファイルに保存 png(out_f, pointsize=13, width=param_fig[1], height=param_fig[2])#出力ファイルの各種パラメータを指定 plot(out, xlab="", ylab="") #ROC曲線をプロット dev.off() #おまじない
Memorandum(自分用の備忘録)
- genefilterパッケージのcolttests関数で、行列のt検定ができる。
rm(list = ls())